Потребность в оценке структур транспортных сетей связи (ТСС), а соответственно и в наличии самой методики оценки, связана с необходимостью выбора оптимальных структур сети еще на стадии их разработки (проектирования).
Наиболее удобным способом описания структуры сети связи является ее задание в виде графа [3]. Если структуры сравниваемых сетей не ориентированы на некоторую базовую структуру, то наиболее полная их оценка может быть получена с использованием численных методов. Это определяется тем, что в условиях дестабилизирующих факторов параметры структур сетей могут существенно отличаться от параметров, полученных в их исходных состояниях. Поэтому в данном случае наиболее удобным способом оценки структур сетей связи в виде графов являются статистические методы, к которым относится метод Монте-Карло [2; 5].
Основная часть
Оценку структур транспортных сетей часто проводили по критерию связности графа сети. На наш взгляд, параметр связности сети достаточно информативно определяется показателем количества остовных деревьев Kост дер, соответствующих графу сети, предлагаемому к рассмотрению, поскольку на сети связи прежде всего важна полная взаимная доступность всех корреспондирующих узлов между собой. Наличие хотя бы одного остовного дерева обеспечивает такую взаимную достижимость, характеризуя самый критический вариант организации связи.
При выборе той или другой структуры ТСС важно прогнозировать их поведение в условиях различных деструктивных воздействий, поэтому оценивать эти структуры предлагается более информативным показателем – суммарным количеством остовных деревьев ![]() , определяемым с помощью метода Монте-Карло. В одном испытании Кост дер вычисляется как минор последнего элемента главной диагонали Мnn матрицы связности исследуемой сети K=[kij] после воздействия (Кост дер = Мnn).
, определяемым с помощью метода Монте-Карло. В одном испытании Кост дер вычисляется как минор последнего элемента главной диагонали Мnn матрицы связности исследуемой сети K=[kij] после воздействия (Кост дер = Мnn).
При оценке сети связи с коммутацией пакетов (КП) параметра связности ее графа оказалось недостаточно. В таких сетях возникает дефицит времени на передачу пакетов трафика реального времени. Так, в сетях с КП даже в исходном их состоянии не все маршруты пригодны для передачи телефонных сигналов, где время задержки сигналов не должно превышать 250 мс [1; 4]. С учетом данного обстоятельства для сетей с КП следует ввести дополнительный параметр, характеризующий структуры сетей.
Вторым параметром, который, на наш взгляд, в наибольшей степени характеризует структуру сети, является кондиционность маршрутов для всех корреспондирующих пар узлов (КПУ) сети. Под кондиционностью маршрута будем понимать время, затрачиваемое на установление телефонной связи (технология с коммутацией каналов (КК)) и время на пересылку пакета той же телефонной связи (технология с КП) по данному маршруту.
Для технологии с КК кондиционный маршрут должен иметь не более 5 транзитных станций в своем составе (таковы требования сети «Памир»).
Как оказалось, найти однозначные оценки параметра кондиционности маршрутов при использовании на сети технологии с КП достаточно сложно. В первую очередь это связано с наличием некоторого множества самих технологий с КП и большого числа производителей оборудования, при использовании которого эти оценки могут существенно отличаться друг от друга. Если предположить, что речевую информацию требуется передать с Дальнего Востока и на Запад России (L=10000 км), то согласно расчетной формуле (1) [1], общее время задержки не превысит требуемое при 3, 4 узлах коммутации.
Тзад = Тр+Тпк+Тпр+Тб, (1)
где: Тр – задержка, определяемая временем распространения электрического сигнала по кабелю связи, проложенному между отправителем и получателем. Оно зависит от типа кабеля и для оптических кабелей равно 5 мкс/км;
Тпк – задержка, определяемая временем, необходимым на выполнение операции преобразования речевого сигнала в цифровой вид и его пакетизацию. Данное время зависит от типа используемого алгоритма преобразования речевого сигнала. Так, например [1], при использовании стандарта G.711 это время равно 30 мс. При использовании других алгоритмов время может увеличиваться;
Тпр – задержка, определяемая временем прохождения пакетов по узлам коммутации транспортной сети. Время задержки зависит от числа различных сетевых устройств, включенных в маршрут прохождения пакетов, а также от времени работы устройств при обработке пересылаемых пакетов. Данный тип задержки в наибольшей степени зависит от используемых технологий, типа сетевого оборудования и возможности его стыковки [1; 4], а также от величины буфера сетевого оборудования в транзитных узлах коммутации. Причем при расчетах необходимо ориентироваться на максимальную величину этой задержки, соответствующую наихудшим условиям функционирования сети при перегрузках (резких всплесках, свойство самоподобия трафика). В среднем данную величину задержки можно оценить в 30 мс, которая, однако, должна уточнятся по реальным сведениям о технологии и возможностям используемых сетевых средств связи;
Тб – задержка, определяемая временем работы устройств на узле получателя. Как и задержка Тпк , она определяется алгоритмами обработки пакетов приемного пункта, а также временем буфера джиттера. Величина задержки данного типа [1] может быть оценена в 40 мс.
Предлагаемая методика оценки является универсальной и позволяет анализировать рассматриваемые структуры как в исходном состоянии, так и при воздействиях различного рода, задаваемых в виде вероятности повреждения ее ребер и узлов. Кроме того, методика позволяет прогнозировать состояние структур сетей и производить их сравнение с учетом возможностей, используемых на ТСС телекоммуникационных технологий.
Исходными данными для работы алгоритма являются:
1) граф транспортной сети, задаваемый матрицей связности ![]() ,
,
где 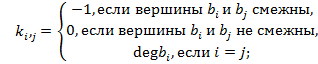 (2)
(2)
2) узлы связи потребителей телекоммуникационных услуг и линии их привязки к узлам коммутации;
3) вероятности повреждения узлов и линий связи (Руз, Рлин);
4) число испытаний, необходимых для работы алгоритма Монте-Карло с требуемой точностью;
5) r - число пунктов транзита (узлов коммутации) в составе кондиционного маршрута сети.
Блочная схема алгоритма оценки структуры транспортной сети приведена на рисунке 1.
Она состоит из следующих блоков и отдельных процедур:
- блока статистических испытаний (метод Монте-Карло),
- блока нахождения маршрутов между требуемыми парами корреспондирующих узлов связи потребителей телекоммуникационных услуг (алгоритм Флойда),
- процедуры нахождения суммарного числа остовных деревьев ![]() ,
,
- процедуры определения поврежденных линий сети связи,
- процедуры вычисления вероятности сохранения связности сетью (pl),
- процедуры оценки кондиционности маршрутов.
В качестве промежуточных данных, необходимых для перехода от работы одного алгоритма к работе другого, следует считать структуры сетей, соответствующие определенным вероятностям связности анализируемой сети.
Ограничение:
при использовании метода Монте-Карло для оценки параметров структур вероятности выхода из строя предполагаемых узлов и линий связи выбирались одинаковыми, поскольку все эти параметры оценки относятся к графу сети:
![]() =
= ![]() , где i(j)=
, где i(j)=![]() и
и ![]() =
= ![]() , где i(j)=
, где i(j)=![]() .
.
Для определения кратчайших путей между всеми парами корреспондирующих узлов использовался специальный алгоритм Флойда, поскольку его сложность составляет O(n3), что на порядок лучше по сравнению с n-кратным применением алгоритма Беллмана-Форда (O(n4)) и экономит 50% времени по сравнению с n-кратным применением алгоритма Дейкстры. В работе определялось по два кратчайших маршрута для каждой КПУ, поскольку они обеспечивают наибольшую живучесть направлений связи.
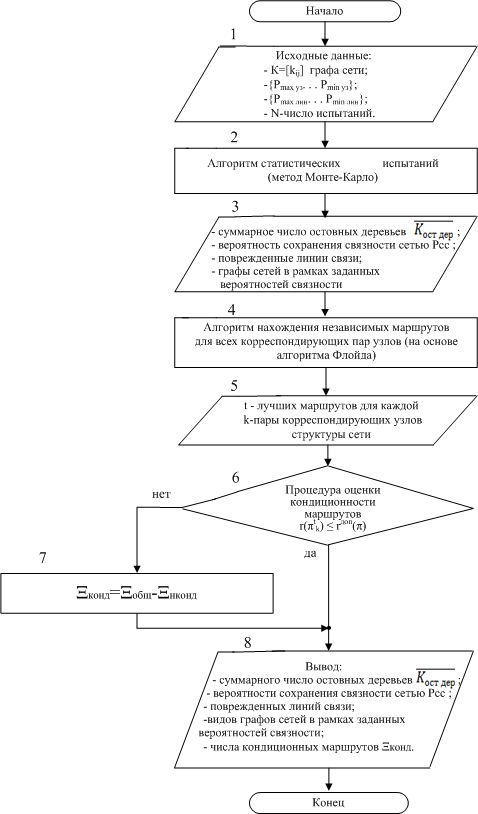
Рис. 1. Блок-схема алгоритма оценки структуры ТСС.
В наибольшей степени сравнительная оценка структур транспортных сетей между собой может быть использована как на этапе планирования, так и при восстановлении связи. При восстановлении связи очень важно понимать, какая из восстановленных линий приводит к лучшей связности сети и прибавляет большее количество кондиционных маршрутов Ξ конд.
По этой причине в качестве примера для сравнения выбраны структуры, отличающиеся дополнительным ребром, вводимым в некоторую базовую сеть. Базовая сеть представлена в виде решетки с числом узлов n=12 и подключенными к ним шестью оконечными узлами связи потребителей телекоммуникационных услуг (рисунок 2а).
Сеть NЕТ11 (рисунок 2б) образована путем введения дополнительного ребра между узлами 14-18, NЕТ12 (рисунок 2в) – между узлами 8-16, NЕТ13 (рисунок 2г) – между узлами 7-18, NЕТ14 (рисунок 2д) – между узлами 8-16 и 7-18, а сеть NЕТ15 (рисунок 2г) – между узлами 9-16 и 7-18.
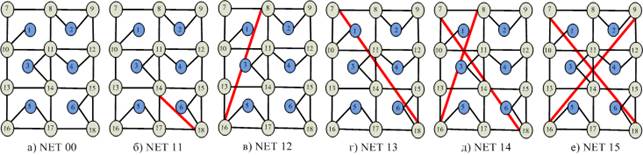
Рис. 2. Исследуемые структуры сетей в виде «решетки».
Вид структур после воздействия представлен на рис. 3 (а-в). Каждому воздействию на узлы и линии будет соответствовать вероятность сохранения связности сетью pl.
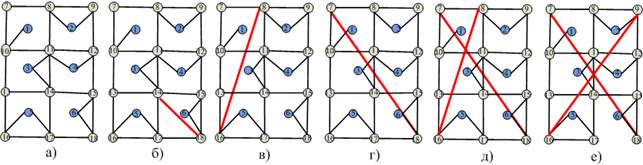
Рис. 3а. Исследуемые структуры сетей в виде «решетки»
при Руз =0,005=const и Pлин=0,01 (pl =0,9).
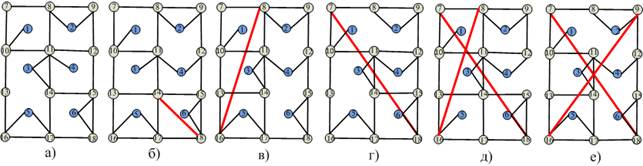
Рис. 3б. Исследуемые структуры сетей в виде «решетки»
при Руз =0,005=const и Pлин=0,12 (pl =0,8).
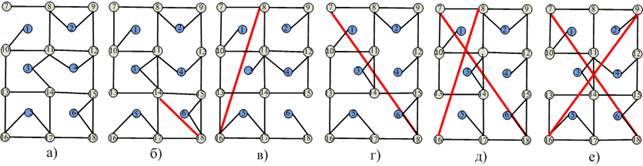
Рис. 3в. Исследуемые структуры сетей в виде «решетки»
при Руз =0,005=const и Pлин=0,19 (pl =0,7).
Вначале оценим суммарную величину остовных деревьев ![]() в различных условиях воздействия на структуры сетей (pl) и определим выигрыш по их числу в зависимости от количества и способа введения дополнительных линий.
в различных условиях воздействия на структуры сетей (pl) и определим выигрыш по их числу в зависимости от количества и способа введения дополнительных линий.
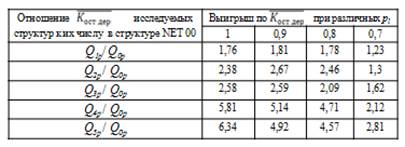
Анализ таблицы 1 показал, что ввод в структуру сети ребра между узлами, образующими путь максимального ранга π(rmax) более чем в 2 раза увеличивает ![]() , т.е. связность максимальна при введении линии между узлами, образующими π(rmax) в данной сети.
, т.е. связность максимальна при введении линии между узлами, образующими π(rmax) в данной сети.
Таблица 1
Выигрыш по ![]() для анализируемых структур при различных воздействиях
для анализируемых структур при различных воздействиях
Результаты оценки структур по параметру кондиционности маршрутов для случая построения таких сетей с использованием технологий КК и КП представлены на
рисунках 4, 5.
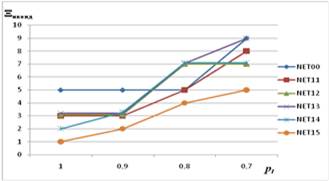
Рис. 4. Зависимость Ξнконд от связности структуры сети (для технологии с КП).
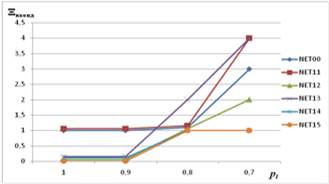
Рис. 5. Зависимость Ξнконд от связности структуры сети (для технологии с КК).
По их данным, технология с КК имеет существенный выигрыш над технологией КП по числу кондиционных маршрутов во всех анализируемых структурах.
Выводы
1. Представленная методика имеет практическое значение в области построения ТСС с использованием современных телекоммуникационных технологий.
2. Методика оценки является универсальной и позволяет анализировать предлагаемые структуры при различных воздействиях на сеть связи.
3. Методика рассчитана на оценку возможностей структур произвольного вида без ограничений на число их узлов и линий, что позволяет использовать ее при разработке структур ТСС для конкретных операций и задач.
4. Найден способ введения дополнительного ребра, приводящий к самым лучшим показателям структуры – ее связности и кондиционности маршрутов.
5. Оценка кондиционности маршрутов структур показала, что она существенно зависит от технологии. В работе определено, что число центров коммутации при передаче речевой информации на сетях с КП должно быть не более 4.
Рецензенты:
Саенко И.Б. д.т.н., профессор, профессор Военной академии связи им. Буденного С.М., г. Санкт-Петербург;
Мякотин А.В., д.т.н., профессор, профессор Военной академии связи им. Буденного С.М., г. Санкт-Петербург.
Библиографическая ссылка
Орлова Л.И. МЕТОДИКА ОЦЕНКИ СТРУКТУР ТРАНСПОРТНЫХ СЕТЕЙ СВЯЗИ ЧИСЛЕННЫМИ МЕТОДАМИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18214 (дата обращения: 12.03.2026).



