В процессе дискретной оптимизации формируются замкнутые множества параметров сложной формы и деревья перспективных μ-подмножеств на основе композиционности подмножеств, состоящие в исключении из базисного множества некоторых неблагоприятных подмножеств и присоединении благоприятных подмножеств, не лежащих в базовом множестве [2]. Организация ветвления основывается на структуре множества, и в качестве множеств ветвления берутся многомерные параллелепипеды. Исходная область разбивается на подмножества, сформированные при различной значности алфавитов случайных величин [1-3]. Разбиение на μ-подмножества формирует μ-деревья, входящие в иерархическое дерево, узлами которых являются μ-подмножества с различной степенью детализации случайных величин [6].
Степень детализации соответствует уровням формируемого μ-дерева. На каждом шаге формирования μ-дерева значность алфавитов возводится в степень 2. Таким же образом изменяется количество μ-подмножеств.
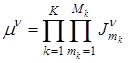 ,
,
где ![]() — уровень μ-дерева (номер шага детализации).
— уровень μ-дерева (номер шага детализации).
Для удобства кодировки получаемых μ-подмножеств и узлов μ-дерева используется кодировка алфавитов случайных величин.
Если диапазон изменения входной величины разбивается на ряд составляющих алфавитов: ![]() , то кодировать каждую составляющую алфавита
, то кодировать каждую составляющую алфавита ![]() можно номером этой составляющей
можно номером этой составляющей ![]() . Например, для узла μ-дерева (3х2) кодировка μ-подмножеств будет иметь вид (рис. 1):
. Например, для узла μ-дерева (3х2) кодировка μ-подмножеств будет иметь вид (рис. 1):
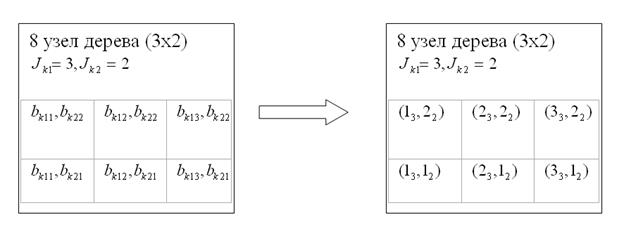
Рис. 1. Кодировка μ-подмножеств узла μ-дерева (3х2) (![]() ).
).
Пример разбиения множества случайных величин на μ-подмножества представлен на рисунке 2.
А)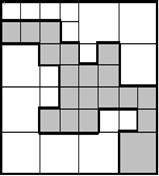 Б)
Б)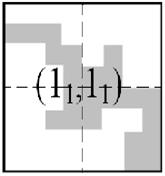 В)
В)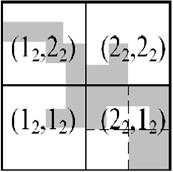
Г)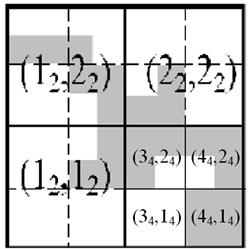 Д)
Д) 
Е)
Рис. 2. Пример разбиения множества случайных величин на μ-подмножества.
Исходный параллелепипед, содержащий все имеющиеся наблюдения, изображен на рис. 2,А. Обозначим эту область ![]() (рис. 2,Б). Ей соответствует корневой узел дерева. Пусть область множества, закрашенная серым цветом, является оптимальной с точки зрения получения требуемых выходных свойств
(рис. 2,Б). Ей соответствует корневой узел дерева. Пусть область множества, закрашенная серым цветом, является оптимальной с точки зрения получения требуемых выходных свойств ![]() [2, 4, 7].
[2, 4, 7].
Светлая область характеризуется возможностью получения некачественных свойств ![]() или отсутствием попадания в нее значений случайных величин (рис. 2,А). При формировании μ-дерева (2х2)
или отсутствием попадания в нее значений случайных величин (рис. 2,А). При формировании μ-дерева (2х2)
(![]() ) на первом шаге область разбивается на 4 μ-подмножества (рис. 2,В), на втором шаге — 16 и т.д.
) на первом шаге область разбивается на 4 μ-подмножества (рис. 2,В), на втором шаге — 16 и т.д.
Задаваемое m - нами пороговое значение точек должно быть превышено в подмножестве. Если это условие не соблюдается, то дальнейшая детализация не может быть выполнена. Процесс прекращается при достижении требуемой точности разбиения. Далее производим возврат на предыдущий уровень для разбиения соседнего многомерного μ-подмножества.
В пустотах, которые остались после отсева, необходимо выделить μ-подмножества, которые обеспечивают получение требуемых свойств с максимальной частотой. Узлы μ-дерева обозначены следующим образом:
○ — соответствующее μ-подмножество с детализацией на уровне;
□ — пустое μ-подмножество без детализации не осуществляется;
■ — μ-подмножество, удовлетворяющее критерию отбора и точности разбиения.
Пунктиром на рисунке 2 обозначено разбиение, с областью шага на 4 μ-подмножества с кодировкой (12,12), (12,22), (22,22), (22,12). Каждому из этих μ-подмножеств соответствуют узлы μ-дерева, расположенные на первом иерархическом уровне (рис 3). Процесс разбиения продолжается для каждого из μ-подмножеств. Подмножества, не удовлетворяющие критерию отбора, считаются пустыми и в дальнейшем рассмотрении не участвуют. Для остальных μ-подмножеств производится такое же разбиение, что и для исходного прямоугольника. Процесс повторяется до тех пор, пока размер μ-подмножества последнего уровня не будет превышать требуемой точности приближения. В частности, μ-подмножество (22,12) разбивается на подмножества (34,14), (34,24), (44,24), (44,14) (рис. 2,Г). В результате формируется оптимальная область случайных величин сложной формы (Рис. 2,Е), μ-дерево которой изображено на рисунке 3. Дерево имеет 3 уровня иерархии, соответствующие заданной степени детализации.
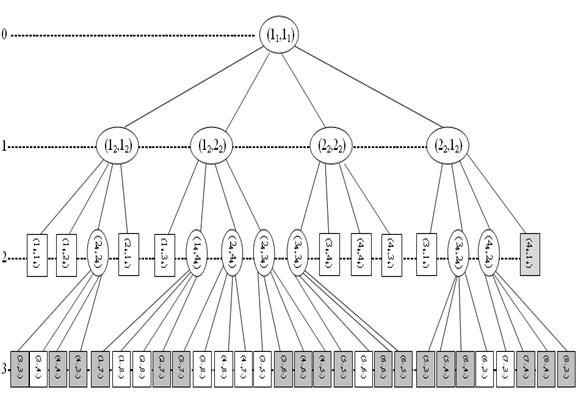
Рис. 3. Вид μ-дерева, сформированного для заданной значности алфавитов случайных величин
Рассмотренный подход формирования иерархического μ-дерева относится к алгоритму построения иерархии «сверху вниз» – от верхних уровней к нижним. Исходная область разбивается на конечное множество μ-подмножеств, из которых формируется замкнутое оптимальное множество сложной формы.
Обратный подход состоит в формировании иерархии «снизу вверх» – от нижних уровней к верхним. В этом случае исходное множество случайных величин разбивается на максимальное число m подмножеств, которое определяется планируемой сложностью формируемого μ-дерева и зависит от количества его уровней. μ-подмножества нижнего уровня объединяются в более крупные. Критериями объединения служат композиционность подмножеств контакт μ-подмножеств между собой по одной или нескольким осям изменения случайных величин и увеличение значения целевой функции при их объединении.
Заключение
Разработан метод формирования пространств параметров сложной формы и μ-деревьев перспективных подпространств на основе композиционности подпространств, состоящий в исключении из базисного пространства некоторых неблагоприятных подмножеств и присоединении благоприятных подмножеств, не лежащих в базовом пространстве. Метод отличается использованием сетки множества μ-подпространств, образованных случайными величинами.
Рецензенты:
Володин И.М., д.т.н., профессор, проректор по научной работе, ФГБОУ ВПО «Липецкий государственный технический университет», г. Липецк;
Шмырин А.М., д.т.н., доцент, заведующий кафедрой высшей математики, ФГБОУ ВПО «Липецкий государственный технический университет», г. Липецк.
Библиографическая ссылка
Корнеев А.М., Абдуллах Л.С., Сметанникова Т.А. ФОРМИРОВАНИЕ ЗАМКНУТЫХ МНОЖЕСТВ ПАРАМЕТРОВ СЛОЖНОЙ ФОРМЫ И ДЕРЕВЬЕВ ПЕРСПЕКТИВНЫХ ПОДМНОЖЕСТВ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18211 (дата обращения: 16.02.2026).



