К транспортным сетям связи предъявляются высокие требования по вероятностно-временным характеристикам, которые можно обеспечить путем выполнения условия кондиционности маршрутов корреспондирующих пар узлов. Под кондиционностью маршрута в данной статье будем понимать время на пересылку пакета речевой информации по данному маршруту.
Проблема заключается в том, что на транспортных сетях связи пакеты с речевой информацией вынуждены проходить большое количество промежуточных центров коммутации, накапливая величину времени задержки. Поэтому уже изначально не все кратчайшие маршруты следования информации между узлами корреспондирующих пар будут удовлетворять требованию кондиционности. Тем более, в условиях изменения структуры сети связи в результате различных деструктивных воздействий, в условиях применения современных телекоммуникационных технологий для построения транспортных сетей связи и фактической потоковой обстановки на них, устанавливать гарантированные соединения для корреспондирующих пар узлов по кондиционным маршрутам становится еще более затруднительным. Решение задачи можно получить путем умелого управления потоковыми ресурсами сети и их оптимальным распределением по кондиционным маршрутам.
Основная часть
Известны и на практике чаще всего используются задачи, в которых требуется определять или максимальную суммарную величину потоков ∑fij=max на сети или удовлетворить требованию по величине потоков, протекающих между заданными узлами корреспондирующих пар.
К сожалению, в решении нашей задачи данные формулировки не могут быть использованы в силу того, что все потоки, образуемые в сети, должны протекать по кондиционным маршрутам. Задача распределения потоков по кондиционным маршрутам формулируется следующим образом.
Заданы: 1) матрица связности графа сети G(n;m);
2) корреспондирующие пары узлов (каждый связан с каждым);
3) емкости ребер сети Cij i,j 
n, i≠j. Под емкостью можно понимать или число каналов или величину суммарного потока, протекающего по данному ребру.
4) параметры кондиционного маршрута, пригодного для передачи сигналов технологий с коммутацией пакетов: rдоп(πkt) – допустимый ранг кондиционного маршрута, где k – номер корреспондирующей пары узлов, t – порядковый номер маршрута, rдоп – допустимое число пунктов транзита (коммутации) в составе кондиционного маршрута сети; или Tзаддоп – допустимая величина задержки на пересылку пакетов информации.
Ограничения: 1) суммарный поток, протекающий по ребру, не может быть больше его емкости ∑fij≤Сij;
2) в процессе решения распределительной задачи следует контролировать наличие образующихся разделительных множеств сети.
Требуется (цель исследования): образовать максимальное множество потоков заданной величины, которые протекают по маршрутам, заданного ранга (по кондиционным маршрутам).
Ниже приводится блочная схема алгоритма распределения информационных потоков по кондиционным маршрутам (рисунок 1). Она включает базовый алгоритм Флойда, задачу коммивояжера и несколько вспомогательных процедур. Алгоритм Флойда относится к классу полиномиальных алгоритмов, а задача коммивояжера к классу NP-полных задач (математический аппарат исследования).
Рассмотрим последовательность работы алгоритма распределения информационных потоков по кондиционным маршрутам на структуре транспортной сети связи.
1. С помощью алгоритма Флойда определяются кратчайшие пути на графе сети для всех корреспондирующих пар узлов (в данном случае узлами корреспондирующих пар являются центры коммутации транспортной сети)
Π={Пk}, Пk={πkt}, k=
, t =
, (1)
где n– число центров коммутации в сети, hсв – наименьшая валентность узла в корреспондирующей паре узлов.
Из существующих алгоритмов определения кратчайших путей на графе для всех корреспондирующих пар узлов выбор сделан в пользу специального алгоритма Флойда. Его сложность составляет O(N3), что на порядок лучше по сравнению с алгоритмом Форда (O(N4)) и экономит 50% времени по сравнению с n-кратным применением алгоритма Дейкстры [1, 3].
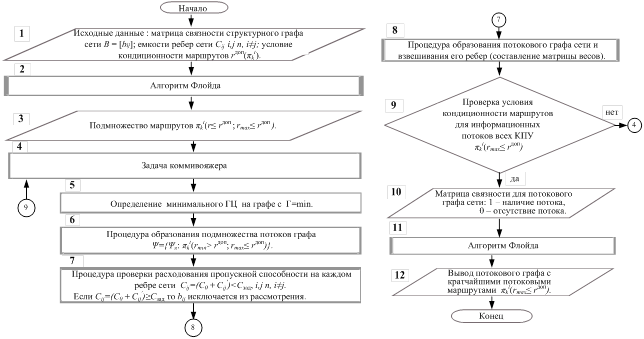
Рис. 1. Блочная схема алгоритма распределения информационных потоков по кондиционным маршрутам
2. Определяются ранги полученных маршрутов r(πkt). В соответствии с выбранной телекоммуникационной технологией для построения транспортной сети связи, типом сетевого оборудования и возможностями его стыковки определяется допустимое число промежуточных центров коммутации на маршрутах передачи информации [2, 4]. Условие кондиционности задается формулой (2)
r(πkt)≤ rдоп(πkt), k=
, t =
, (2)
3. Все кратчайшие маршруты, удовлетворяющие условию кондиционности, насыщаются единичными потоками.
Образуется подмножество потоков Ψ графа сети такое, что потоки в нем протекают по кондиционным маршрутам
Ψ={Ψπ: πkt(r≤ rдоп)}. (3)
4. Распределение информационных потоков по маршрутам не удовлетворяющим заданному условию кондиционности для структурного графа производится благодаря определению минимальных гамильтоновых циклов на нем. (Процедура образования подмножества потоков Ψ графа, которые протекают по маршрутам π(r> rдоп)):
Ψ={Ψπ: πkt(r> rдоп)}. (4)
Минимальные гамильтоновы циклы на графе определяются с помощью задачи Коммивояжера. Ее работа основана на представлении потоковой обстановки на транспортной сети связи в виде многослойного графа 
. Каждый минимальный гамильтонов цикл, входящий в состав моделируемой сети, называется слоем, подграфом 
графа 
.
5. В качестве исходных данных для работы задачи коммивояжера задается матрица связности между узлами графа сети B=║bij║, где элементы матрицы определяются следующим образом:
bij = 
(5)
где 0 и 1 – это веса ребер графа, описывающего структуру транспортной сети связи.
Такие веса приписываются ребрам графа сети при определении первого минимального гамильтонова цикла, для всех последующих подграфов веса ребер будут иными.
6. После составления матрицы связности программой IIG [5] рассчитывается минимальный гамильтонов цикл, который определяет первый слой многослойного графа. Ребра графа, вошедшие во множество полученных на данном минимальном гамильтоновом цикле маршрутов, равномерно «заполняются» единичными потоками.
Для всех последующих итераций составления многослойного графа исходными данными выступают величины потоков, задаваемые в матрице весов. Процедура взвешивания проводится после получения очередного минимального гамильтонова цикла. Весовые коэффициенты назначаются в соответствии с величиной потока, распределенного по ребру на предыдущем шаге, но независимо от проведенного на предыдущем шаге взвешивания, т.е. каждый раз новые. (Процедура образования потокового графа и взвешивания его ребер).
В процессе составления матрицы весов необходимо контролировать расходование пропускной способности на каждом ребре:
Cij=(C0 + Cij')<Cзад, i,j 
n, i≠j. (6)
Если Cij=(C0 + Cij')≥Cзад то bij исключается из рассмотрения. (Процедура проверки расходования пропускной способности на каждом ребре сети).
7. При распределении потоков на полученном минимальном гамильтоновом цикле важно определить порядок насыщения ребер графа по маршрутам, соединяющим узлы корреспондирующих пар. В приоритете соединение наиболее удаленных узлов корреспондирующих пар при условии коммутации в некоторых промежуточных центрах, число которых определяется условием кондиционности маршрутов. С этой целью устанавливаются прямые («сквозные») соединения на определенных участках сети по конкретным информационным потокам. В рамках данной статьи будем называть такие участки потоковыми маршрутами. Потоковый маршрут будет соединять два центра коммутации транспортной сети связи через определенное число промежуточных центров коммутации, в которых будет отсутствовать обработка адресов сообщений по заданному информационному потоку. Запрет на обработку может быть установлен вручную или реализован программно в коммутационном оборудовании.
8. После распределения информационных потоков для всех корреспондирующих пар узлов с соблюдением условия πkt(rmax≤ rдоп) составляется потоковый граф. Он задается матрицей связности, в которой наличие потока обозначается 1, отсутствие потока – 0. Применение к нему алгоритма Флойда дает возможность определить кратчайшие потоковые маршруты. В случае если информационные потоки распределены не для всех корреспондирующих пар узлов, работа возвращается к алгоритму коммивояжера.
9. Алгоритм распределения потоков по кондиционным маршрутам завершает работу выводом потокового графа с кратчайшими потоковыми маршрутами, которые являются кондиционными.
Вывод: таким образом, переход от распределения кратчайших маршрутов на структуре графа сети к распределению кратчайших маршрутов на потоковом графе позволит сократить время задержки на обработку сигналов сетевым оборудованием промежуточных центров коммутации до требуемого по условию кондиционности маршрутов, и тем самым позволит передавать речевую пакетную информацию с заданным уровнем качества.
Рецензенты:
Саенко И.Б. д.т.н., профессор, профессор Военной академии связи им. Буденного С.М., г. Санкт-Петербург;
Мякотин А.В., д.т.н., профессор, профессор Военной академии связи им. Буденного С.М., г. Санкт-Петербург.
Библиографическая ссылка
Орлова Л.И. РАСПРЕДЕЛЕНИЕ ПОТОКОВ РЕЧЕВОЙ ИНФОРМАЦИИ ПО КОНДИЦИОННЫМ МАРШРУТАМ ТРАНСПОРТНОЙ СЕТИ СВЯЗИ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18156 (дата обращения: 19.04.2024).