Механические системы, состоящие из связанных маятников, являются составной частью технических конструкций, находящих широкое применение в различных областях деятельности человека. Со временем в связи с изношенностью механической системы ее физические параметры могут менять свои значения. Поэтому определение характеристик механической системы важно для проверки надежности ее работы. Об этих характеристиках чаще всего можно судить после разборки устройства, но этот процесс может быть трудоемким, дорогостоящим и может привести к нарушению приработки деталей системы. Поэтому в настоящее время получило широкое развитие направление, возникшее на стыке теории механизмов с акустикой, решающее задачи безразборной диагностики технических конструкций [3, 4, 6 – 8, 10].
Свободные колебания механических систем, в том числе систем из связанных маятников, рассмотрены во многих трудах по теории колебаний, например, в работах [1, 2, 9]. Но в них рассматриваются прямые задачи по определению частот колебаний системы. В представленной работе поставлены, исследованы и решены обратные задачи – задачи диагностирования характеристик системы по известным частотам ее свободных колебаний.
1. Определение частот колебаний системы из связанных маятников
Рассмотрим механическую систему из трех связанных маятников, соединенных между собой пружинами (рисунок 1).
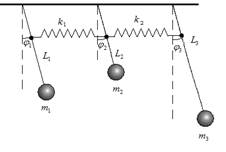
Рис.1. Механическая система из трех связанных маятников
Здесь: ![]() ,
, ![]() ,
, ![]() – массы грузов,
– массы грузов, ![]() ,
,![]() ,
,![]() – длины стержней,
– длины стержней, ![]() ,
, ![]() ,
, ![]() – углы поворотов (обобщенные координаты),
– углы поворотов (обобщенные координаты), ![]() ,
, ![]() – жесткости соединяющих стержни пружин. На каждый из маятников действует момент силы тяжести. Пружины создают дополнительные моменты, величины которых зависят от разности угловых координат маятников.
– жесткости соединяющих стержни пружин. На каждый из маятников действует момент силы тяжести. Пружины создают дополнительные моменты, величины которых зависят от разности угловых координат маятников.
Для вывода уравнений колебаний маятников используем основное уравнение динамики вращательного движения твердого тела вокруг неподвижной оси [9]:
![]() (1)
(1)
где ![]() – моменты инерции тел,
– моменты инерции тел, ![]() – угловые ускорения тел,
– угловые ускорения тел, ![]() – моменты силы тяжести маятников (
– моменты силы тяжести маятников (![]() ). Подставим значения моментов инерции тел, моментов сил тяжести в (1) и получим уравнения движения маятников:
). Подставим значения моментов инерции тел, моментов сил тяжести в (1) и получим уравнения движения маятников:
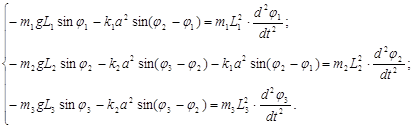 (2)
(2)
Так как рассматриваются малые колебания маятников, поэтому считаем, что ![]() . Тогда с помощью преобразований последнюю систему приведем к виду:
. Тогда с помощью преобразований последнюю систему приведем к виду:
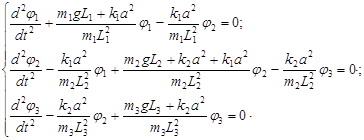 (3)
(3)
Учитывая, что механическая система совершает свободные колебания, принимаем решения системы уравнений (3) в виде [9]: ![]() (
(![]() , где
, где ![]() – частота,
– частота, ![]() – амплитуды колебаний. Подставляя
– амплитуды колебаний. Подставляя ![]() в систему (3), получим следующую систему уравнений:
в систему (3), получим следующую систему уравнений:
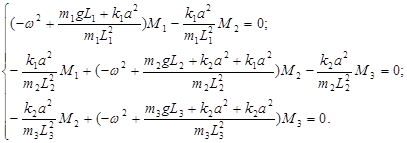
Приравнивая определитель матрицы полученной системы к нулю, найдем уравнение:
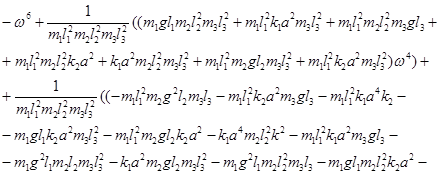
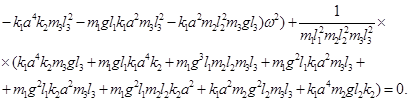 (4)
(4)
Уравнение (4) является частотным уравнением свободных колебаний механической системы из трех связанных маятников. Определение частот колебаний системы рассмотрим на конкретном примере.
Пример 1. Найти собственные частоты колебаний системы из трех связанных маятников, для которой известны параметры: L1=1,168 м, L2=0,556 м, L3=0,824 м, m1=0,25 кг, m2=0,21 кг, m3=0,27 кг., a=0,5м, k1=1,5 Н/м, k2=1 Н/м.
Решение. Подставляя заданные параметры в частотное уравнение (4), получим:
![]() .
.
Корни уравнения, найденные с помощью ЭВМ, следующие: ![]() ,
, ![]() ,
, ![]() . Значит, имеем частоты колебаний:
. Значит, имеем частоты колебаний: ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
2. Задача диагностирования характеристик системы из связанных маятников
Поставим к прямой задаче обратную – задачу диагностирования характеристик системы из связанных маятников по известным частотам ее колебаний. К диагностируемым характеристикам отнесем, например, жесткости соединяющих стержни пружин, массы грузов системы.
Исследуем вначале обратную задачу диагностирования жесткостей пружин. При решении прямой задачи было получено уравнение (4), которое преобразуем к виду:
![]() (5)
(5)
Здесь:
![]()
![]()
![]()
![]()
![]()
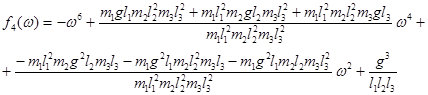
Исследуем вопрос о единственности решения поставленной обратной задачи [6]. Введем некоторые обозначения. Задачу с частотным уравнением (5) и жесткостями ![]() и
и ![]() связывающих пружин обозначим через
связывающих пружин обозначим через ![]() , а задачу с подобным частотным уравнением и массовыми параметрами, но с другими жесткостями
, а задачу с подобным частотным уравнением и массовыми параметрами, но с другими жесткостями ![]() и
и ![]() , обозначим через
, обозначим через ![]() . Частотное уравнение задачи
. Частотное уравнение задачи ![]() имеет вид:
имеет вид:
![]() (6)
(6)
Покажем справедливость следующей теоремы.
Теорема 1. Если собственные частоты задач ![]() и
и ![]() с характеристическими определителями
с характеристическими определителями ![]() и
и ![]() совпадают с учетом их кратностей, то
совпадают с учетом их кратностей, то ![]() и
и ![]() .
.
Доказательство. Заметим, что собственные частоты задачи ![]() являются корнями целой функции [5] – частотного уравнения (5), а собственные частоты задачи
являются корнями целой функции [5] – частотного уравнения (5), а собственные частоты задачи ![]() – корнями уравнения (6). Причем функции
– корнями уравнения (6). Причем функции ![]() (
(![]() ) не зависят от коэффициентов жесткостей пружин и образуют систему линейно независимых функций.
) не зависят от коэффициентов жесткостей пружин и образуют систему линейно независимых функций.
Поскольку функции ![]() и
и ![]() являются целыми функциями от
являются целыми функциями от ![]() и не равны тождественно нулю, то получаем, что функции
и не равны тождественно нулю, то получаем, что функции ![]() и
и ![]() восстанавливаются по своим нулям с точностью до постоянного множителя
восстанавливаются по своим нулям с точностью до постоянного множителя ![]() . Значит,
. Значит, ![]() . Из линейной независимости функций
. Из линейной независимости функций ![]() (
(![]() ) и последнего равенства имеем:
) и последнего равенства имеем: ![]() . Значит,
. Значит, ![]() и
и ![]() . Теорема доказана.
. Теорема доказана.
Рассмотрим метод нахождения жесткостей ![]() и
и ![]() , связывающих грузы пружин по известным двум частотам колебаний механической системы. Если даны две собственные частоты
, связывающих грузы пружин по известным двум частотам колебаний механической системы. Если даны две собственные частоты ![]() и
и ![]() , то уравнения (5) представляют собой систему алгебраических уравнений с двумя неизвестными
, то уравнения (5) представляют собой систему алгебраических уравнений с двумя неизвестными ![]() и
и ![]() :
:
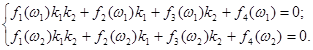 (7)
(7)
Из системы уравнений (7) можно получить аналитические выражения для коэффициентов жесткостей пружин в виде:
![]()
![]()
![]() (8)
(8)
Таким образом, если известны две собственные частоты колебаний системы из трех связанных маятников, то жесткости соединяющих грузы пружин находятся по формулам (8).
Рассмотрим теперь метод нахождения жесткостей пружин по известным трем частотам колебаний механической системы. Сначала решается система уравнений (7) при известных собственных частотах ![]() ,
, ![]() . В результате получим две пары решений относительно коэффициентов жесткостей
. В результате получим две пары решений относительно коэффициентов жесткостей ![]() и
и ![]() . Аналогично решается система вида (7) при известных значениях частот
. Аналогично решается система вида (7) при известных значениях частот ![]() ,
, ![]() , которая также имеет две пары решений. Общим решением двух систем уравнений является лишь один набор значений (
, которая также имеет две пары решений. Общим решением двух систем уравнений является лишь один набор значений (![]() ;
; ![]() ), который и будет искомым.
), который и будет искомым.
Пример 2. Даны частоты ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() колебаний механической системы из трех связанных маятников, а также параметры: L1=1,168 м, L2=0,556 м, L3=0,824 м, m1=0,25 кг, m2=0,21 кг, m3=0,27 кг., a=0,5м. Определить соответствующие жесткости пружин.
колебаний механической системы из трех связанных маятников, а также параметры: L1=1,168 м, L2=0,556 м, L3=0,824 м, m1=0,25 кг, m2=0,21 кг, m3=0,27 кг., a=0,5м. Определить соответствующие жесткости пружин.
Решение. Система уравнений (8) при частотах ![]() и
и ![]() примет вид:
примет вид:
![]()
Решение системы, найденное с помощью ЭВМ:![]()
Подставляя теперь в уравнение (7) частоты колебаний ![]() и
и ![]() получим:
получим:
![]()
Имеем решение: ![]()
Сравнивая полученные решения двух систем уравнений, видим, что общим для них является лишь один набор переменных ![]()
![]() , который и является искомым. Значит, имеем жесткости пружин: k1=1,5 Н/м, k2=1 Н/м
, который и является искомым. Значит, имеем жесткости пружин: k1=1,5 Н/м, k2=1 Н/м
Эти же значения жесткостей можно получить, подставляя заданные частоты и физические параметры механической системы в аналитические формулы (8). Заметим, что значения жесткостей пружин определены верно, так как по решению прямой задачи именно данным физическим параметрам и жесткостям пружин соответствуют заданные значения собственных частот колебаний механической системы.
Поставим теперь обратную задачу диагностирования масс грузов рассматриваемой системы из трех связанных маятников. Частотное уравнение (4) преобразуем к виду:
![]() (9)
(9)
в котором функции ![]()
![]() выражаются через физические параметры системы и частоты ее колебаний.
выражаются через физические параметры системы и частоты ее колебаний.
Так же как и при диагностировании жесткостей пружин исследована единственность решения поставленной задачи. При этом: ![]() – задача с массами
– задача с массами ![]() ,
, ![]() ,
, ![]() и частотным уравнением (9),
и частотным уравнением (9), ![]() – задача с массами
– задача с массами ![]() ,
, ![]() ,
, ![]() и частотным уравнением:
и частотным уравнением:
![]()
Доказана теорема.
Теорема 2. Если собственные частоты задач ![]() и
и ![]() с характеристическими определителями
с характеристическими определителями ![]() и
и ![]() совпадают с учетом их кратностей, то
совпадают с учетом их кратностей, то ![]() ,
, ![]() и
и ![]() .
.
Из теоремы следует, что массы грузов механической системы можно восстановить единственным образом по известным значениям собственных частот колебаний.
Пример 3. Определить массы грузов системы из трех связанных маятников при известных частотах ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() колебаний и параметрах: L1=1,168 м, L2=0,556 м, L3=0,824 м, a=0,5м, k1=1,5 Н/м, k2=1 Н/м.
колебаний и параметрах: L1=1,168 м, L2=0,556 м, L3=0,824 м, a=0,5м, k1=1,5 Н/м, k2=1 Н/м.
Решение. Подставим заданные параметры и частоты колебаний в уравнение (9), получим систему уравнений:
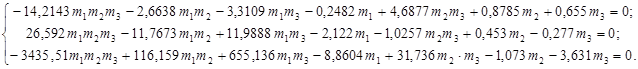
С помощью ЭВМ находим, что полученная система уравнений имеет единственное с физической точки зрения решение: m1=0,25 кг, m2=0,21 кг, m3=0,27 кг.
Заключение
В работе исследована прямая задача определения частот свободных колебаний механической системы из трех связанных маятников. Впервые поставлены обратные задачи – задачи диагностирования характеристик системы из связанных маятников по известным частотам ее свободных колебаний. Решены задачи диагностирования коэффициентов жесткостей пружин и масс грузов системы. Исследована единственность решения задач, доказаны соответствующие теоремы. Предложены методы решения задач, использующие две и три частоты колебаний механической системы. Приведены примеры решений обратных задач.
Методы решений обратных задач можно использовать при исследовании проблемы сохранения безопасных частот колебаний рассматриваемой системы при изменениях ее физических параметров. Кроме того, приведенные методы решений обратных задач можно распространить и на системы из четырех и более маятников, соединенных между собой пружинами.
Рецензенты:
Урманчеев С.Ф., д.ф.-м.н., профессор, директор, Федеральное государственное бюджетное учреждение науки Институт механики им. Р.Р. Мавлютова Уфимского научного центра РАН, г. Уфа;
Ахтямов А.М., д.ф.-м.н., профессор, зав. кафедрой механики сплошных сред, Федеральное государственное бюджетное учреждение высшего профессионального образования «Башкирский государственный университет», г. Уфа.
Библиографическая ссылка
Сафина Г.Ф. ДИАГНОСТИРОВАНИЕ ХАРАКТЕРИСТИК МЕХАНИЧЕСКОЙ СИСТЕМЫ ИЗ СВЯЗАННЫХ МАЯТНИКОВ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18150 (дата обращения: 13.02.2026).



