Ниже приводятся алгоритмы ретроспективного анализа данных нормального функционирования эргатической системы.
1. Оперативная концептуальная модель
Алгоритм основывается на сглаживании реализаций процессов
![]() ,
,
![]() .
.
Для сглаживания используется метод осреднения ординат указанных кривых (реализаций) на некотором интервале около данного ![]() , то есть определение так называемой скользящей средней.
, то есть определение так называемой скользящей средней.
Здесь оценка математического ожидания случайного процесса ![]() определяется по одной реализации
определяется по одной реализации ![]() :
:
![]() .
.
Разбив интервал ![]() на
на ![]() равных частей и применяя для вычисления интеграла формулу прямоугольников, получим:
равных частей и применяя для вычисления интеграла формулу прямоугольников, получим:
![]() . (1)
. (1)
Интервал ![]() выбирался так, чтобы в интервале длиной
выбирался так, чтобы в интервале длиной ![]() с центром в точке
с центром в точке ![]() математическое ожидание
математическое ожидание ![]() было приблизительно линейно (более строго требуется также малость среднего значения корреляционной функции
было приблизительно линейно (более строго требуется также малость среднего значения корреляционной функции ![]() в квадрате с центром в точке
в квадрате с центром в точке ![]() и стороной
и стороной ![]() ).
).
Таким образом, алгоритм определения оперативной концептуальной модели основывается на формуле (1).
2. Идеальная концептуальная модель
Идеальная концептуальная модель характеризует оптимальное управление (идеальная траектория). Она может быть получена усреднением случайной функции ![]() как по времени, так и по ансамблю
как по времени, так и по ансамблю ![]() реализаций:
реализаций:
![]()
или
![]() .
.
На этой формуле и основывается алгоритм определения идеальной концептуальной модели.
Одним из возможных способов определения ![]() по нескольким реализациям является одновременное сглаживание всех реализаций. При применении этого способа все реализации случайной функции строятся на одном графике (при правильно выбранном масштабе эти реализации образуют отчетливую полосу). Средняя линия этой полосы (грубо определяется на газ) и даст оценку математического ожидания
по нескольким реализациям является одновременное сглаживание всех реализаций. При применении этого способа все реализации случайной функции строятся на одном графике (при правильно выбранном масштабе эти реализации образуют отчетливую полосу). Средняя линия этой полосы (грубо определяется на газ) и даст оценку математического ожидания ![]() . Способ глазомерного сглаживания обладает большой простотой, но является субъективным. Предыдущий метод лишен этого недостатка.
. Способ глазомерного сглаживания обладает большой простотой, но является субъективным. Предыдущий метод лишен этого недостатка.
3. Прямое преобразование Фурье
Пусть:
![]() – длительность реализации,
– длительность реализации, ![]() – значения временных рядов,
– значения временных рядов,![]() – число значений,
– число значений,
![]() – интервал дискретизации по времени,
– интервал дискретизации по времени, ![]() .
.
Тогда в соответствии с
![]() ,
,
![]()
и с использованием формул Эйлера можно получить следующие формулы для вычисления коэффициентов прямого преобразования Фурье:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4. Спектральные плотности входного и выходного сигналов; взаимная спектральная плотность
Основываются на использовании прямого преобразования Фурье сигналов ![]() и
и ![]() , а именно:
, а именно:
![]() ,
,
![]() ,
,
![]() .
.
Сглаживание спектральных плотностей производилось по методу Хеннинга:
![]() ,
,
![]() ,
,
![]() .
.
5. Обобщенная частотная характеристика
Здесь определяется с использованием трендов входных и выходных процессов. Обобщенная характеристика получается как характеристика эквивалентной разомкнутой системы с входом ![]() и выходом
и выходом ![]() .
.
В качестве ![]() принимался один из сигналов
принимался один из сигналов ![]() . При определении перекрестных связей между каналами пространственного движения в качестве
. При определении перекрестных связей между каналами пространственного движения в качестве ![]() принимались и некоторые другие фазовые координаты, их скорости или ускорения. В качестве входных процессов при предварительных исследованиях ограничивались
принимались и некоторые другие фазовые координаты, их скорости или ускорения. В качестве входных процессов при предварительных исследованиях ограничивались
![]() .
.
Алгоритмы основывались на использовании спектральных плотностей
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Эффективное подавление случайных ошибок при оценивании частотных характеристик переходных процессов (рассматриваются тренды) достигается осреднением по ансамблю оценок, вычисленных по ансамблю независимых реализаций входных и выходных переходных процессов.
6. Управляющие движения оператора
Определяются путем центрирования ![]() :
:
![]() .
.
7. Спектральные характеристики управляющих движений
Основаны на определении прямого преобразования Фурье процесса ![]() , а именно:
, а именно:
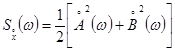 ,
,
![]() ,
,
![]() .
.
8.Автокорреляционная функция управляющих движений
Основывается на реализации формулы
![]() ,
,
где ![]() – интервал корреляции.
– интервал корреляции.
9. Обобщенная частотная характеристика
Основывается на использовании прямого преобразования Фурье сигналов ![]() и
и ![]() , где в качестве
, где в качестве![]() принимается один из сигналов
принимается один из сигналов ![]() , а в качестве
, а в качестве ![]() –
– ![]() .
.
Собственно, алгоритм аналогичен алгоритму определения частотной характеристики по трендам.
10. Распределение вероятностей частот в управляющих движениях
Пусть ![]() –
– ![]() -я реализация управляющих движений,
-я реализация управляющих движений,![]() – интервал реализации.
– интервал реализации.
Известно [3]
![]()
(определяет плотность вероятности случайной величины ![]() в процессе
в процессе ![]() ):
):
![]() ).
).
При этом ![]() представляет собой дисперсию, приходящуюся на участок частот
представляет собой дисперсию, приходящуюся на участок частот ![]() , прилежащий к точке
, прилежащий к точке ![]() . Тогда
. Тогда
![]()
определяет среднюю амплитуду гармоник с частотой ![]() в управляющих движениях.
в управляющих движениях.
Отметим, что в силу методических и вычислительных погрешностей ![]() не будет равняться единице. Поэтому возникает необходимость нормировки, полагая
не будет равняться единице. Поэтому возникает необходимость нормировки, полагая
![]() .
.
Величина ![]() выражает вероятность попадания в интервал
выражает вероятность попадания в интервал ![]() . Откуда
. Откуда
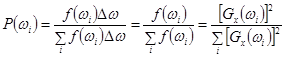 .
.
Определение ![]() и
и ![]() включает:
включает:
- задание ![]() ;
;
- вычисление ![]() ;
;
- вычисление ![]() ;
;
- вычисление 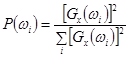 ;
;
- вычисление ![]() .
.
При всей кажущейся простоте использованных на практике алгоритмов, получение указанных характеристик не столь тривиально. Требуется опыт и инженерная интуиция. Получение результатов, как правило, связано с широким использованием итеративных методов.
Предложенные алгоритмы прошли многостороннюю апробацию при разработке тренажеров для подготовки операторов эргатических систем различного назначения [1…8].
Рецензенты:
Родионов Ю.В., д.т.н., профессор, декан автомобильно-дорожного института ПГУАС, заведующий кафедрой эксплуатации автомобильного транспорта, г. Пенза;
Кошев А.Н., д.х.н., профессор, профессор кафедры информационно-вычислительных систем Пензенского государственного университета архитектуры и строительства, г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Нашивочников В.В. АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ НОРМАЛЬНОГО ФУНКЦИОНИРОВАНИЯ ЭРГАТИЧЕСКОЙ СИСТЕМЫ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18139 (дата обращения: 27.02.2026).



