Озабоченность университетов европейского союза падением уровня математической подготовки школьников [1] заставляет чиновников на разных уровнях принимать меры для решения этой проблемы. Тенденции к ослаблению математических знаний у школьников наблюдаются и в России (по результатам единого государственного экзамена (ЕГЭ) по математике). Тем не менее до сих пор в мире российское высшее образование отличается своей фундаментальностью. Несмотря на непрекращающиеся реформы образования и сменяющие друг друга ФГОСы, упования на самостоятельность обучения студентов и сокращение контактных часов, что ведет к сжатию тематического плана дисциплин, математическая подготовка инженеров не претерпела кардинальных изменений. Студенты продолжают учиться доказывать теоремы, решать не только вычислительные, но и понятийные задачи, и в первые семестры любой инженерной специальности как минимум четверть учебного времени посвящена изучению математики. В связи с растущей интенсивностью изучения одной из сложнейших дисциплин образовательной программы – математического анализа, и отсутствием внешних механизмов стимулирования студентов к самообучению, вузы вынуждены искать внутренние ресурсы для повышения эффективности обучения студента. В данной работе обсуждаются два способа оценивания работы студентов, проводится сравнительный анализ этих методов и их эффективность. Исследуются оценки различных групп студентов (от 40 до 70 человек), обучающихся по направлениям, связанных с информационными технологиями за 5-летний период. Программа дисциплины «математический анализ» за это время не изменялась.
После начала эксперимента по введению обязательного ЕГЭ по математике, преподаватели-математики отмечали падение уровня школьной подготовки по математике у первокурсников, формировалось недоверие к ЕГЭ. Проблеме влияния ЕГЭ по математике на успеваемость в вузе посвящены исследования [2,5], где делается вывод об адекватности данного вида экзамена для использования его в качестве вступительного. Тем не менее центры качества образования различных вузов, в том числе и в Томском политехническом университете (ТПУ), продолжают мониторить принимаемый в вуз контингент. В частности, в ТПУ был разработан входной тест по школьной математике, который в обязательном порядке выполняют все студенты первокурсники в первые дни семестра. По результатам входного тестирования преподаватели имеют возможность посоветовать студентам либо выбрать траекторию усиленного фундаментального образования (элитное), либо воспользоваться дополнительными (адаптационными) занятиями для ликвидации пробелов школьного образования. Отметим, что программа всех траекторий одинакова и отличается лишь глубиной изучения математического анализа. Первый возникающий вопрос: является ли входной тест более информативным, чем ЕГЭ? В таблице 1 приведены коэффициенты корреляции результатов ЕГЭ по математике и входного тестирования, а также корреляция этих тестов с оценкой по математическому анализу за 1-ый семестр. Не углубляясь в статистический анализ, отметим, что связь результатов ЕГЭ и успешного освоения первой математической дисциплины весьма слабая, в то же время связь результатов входного тестирования и результатов экзамена несколько сильнее, но также далека от единицы. Необходимо отметить, что цель входного тестирования – выявить пробелы именно по тем разделам математики, без которых студенту невозможно освоить университетские математические дисциплины. Т.е. идентичности результатов входного теста и ЕГЭ ожидать не следует. Тем не менее практика показала, что единичные случаи отличия результатов этих двух тестов в 70–80 баллов по 100-балльной шкале говорят о безнадежности первокурсника.
Таблица 1
Коэффициенты линейной корреляции между результатами ЕГЭ (математика), входного тестирования и оценкой экзамена в 1-ом семестре по математическому анализу.
|
|
Входной тест и ЕГЭ |
Входной тест и экзамен |
ЕГЭ и экзамен |
|
2009 |
0,51 |
0,52 |
0,31 |
|
2010 |
0,40 |
0,46 |
0,34 |
|
2012 |
0,57 |
0,62 |
0,27 |
|
2013 |
0,48 |
0,4 |
0,38 |
Заметим, что исследуемая выборка студентов имеет баллы ЕГЭ по математике на уровне среднего среди Российских вузов [4]. В таблице 2 приведены результаты ЕГЭ по математике и среднего балла ЕГЭ по трем предметам, требуемых при зачислении на выбранное направление обучения (русский язык, математика, физика/информатика). В качестве ориентира, на который следует равняться в плане организации математической подготовки инженеров, мы повсеместно используем МГТУ им. Баумана. Поэтому в таблице 2 также приведены средние баллы ЕГЭ этого вуза.
Таблица 2
Средние баллы ЕГЭ по математике и по трем предметам (русский язык, математика, физика/информатика)
|
|
По России (математика) |
По выборке студентов (математика) |
Среднее по трем предметам ТПУ [4] |
Среднее по трем предметам МГТУ им. Баумана [4] |
|
2009 |
43.6 |
62.9 |
72.1 |
71.1 |
|
2010 |
43.7 |
68.3 |
66.7 |
68.2 |
|
2011 |
47.5 |
|
68.1 |
76.1 |
|
2012 |
44.6 |
65.1 |
66.6 |
73.1 |
|
2013 |
49.6 |
74.1 |
72.4 |
76.9 |
|
2014 |
39.6 |
72.3 |
68.3 |
72.1 |
Для характеристики успеваемости студента и мониторинга его активности в течение семестра в ТПУ введена рейтинговая система. В то же время она играет роль регулятора готовности студента к сдаче экзамена – зачета. Систему рейтинговых баллов преподаватель устанавливает индивидуально. В данном исследовании рейтинговыми баллами являются баллы контрольных точек – контрольные работы, индивидуальные задания, коллоквиумы. Оценка на экзамене имеет 10-балльную шкалу. Положительной считается оценка 5 и выше. В первые два исследуемых года – 2009-ый и 2010-ый – работа в семестре (накопленный рейтинговый балл) никак не влиял на оценку на экзамене. На рисунке 1 приведены гистограммы семестровых рейтинговых и итоговых экзаменационных баллов 2009 и 2012 годов.
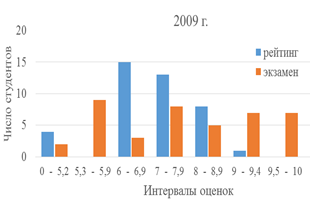
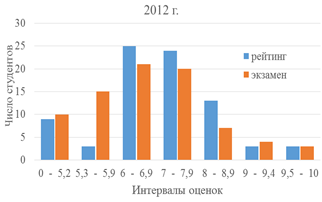
Рис. 1. Гистограммы распределения рейтинговых и экзаменационных баллов
Как видно на диаграмме 2009 г., работа студентов в семестре в среднем слабо коррелирует с оценкой на экзамене. Работа по подготовке к экзамену многими студентами проводилась только в период сессии. Слабые, но трудоспособные студенты, работая в семестре, на экзамене успеха не имели. В то же время студенты с хорошим потенциалом могли в семестре ничего не делать, но быть успешными на экзамене. Как правило, подобное отношение сильных студентов к математическому анализу в 1-ом семестре приводило к провалу во втором, и мы ежегодно имели несколько человек, повторяющих курс или отчисляющихся после 1-го курса.
Начиная с 2011 года в ТПУ было принято решение перейти на накопительную систему итоговой экзаменационной оценки, которая складывалась из рейтинговых баллов семестра (60 %) и баллов экзамена (40 %). Изменения в перераспределении оценок можно видеть на гистограмме 2012 г. рис. 1. С одной стороны, это поддерживает слабых и вдохновляет на равномерную работу всех студентов, а амбициозного и ориентированного на отличный результат мотивирует на подготовку к каждой контрольной точке. С другой стороны, проявляется тенденция «работы за баллы». В любом случае, изменения в системе оценивания несколько повышает мотивацию студентов. Наилучшие результаты мотивированности мы наблюдали у иностранных студентов (рис. 2).
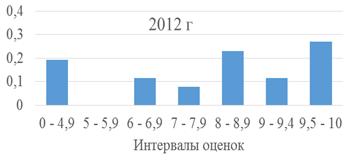
Рис. 2. Гистограмма частот рейтинговых семестровых баллов иностранных студентов
Как отмечалось в работе [3], студенты, обучающиеся по программам межгосударственных соглашений и имеющие существенные материальную (государственные стипендии уровня преподавательских зарплат) и социальную поддержку (гарантировано трудоустройство в ведущей в стране фирме), работают много и эффективно. Как видно из рисунка 2, частотное распределение результатов текущей семестровой работы смещено в сторону максимальных оценок. Экзамены, как правило, такие студенты сдают только на хорошо и отлично. В то же время иностранные студенты, обучающиеся на общих основаниях, работают и успевают очень слабо. На рис. 2 в правой части гистограммы присутствует столбец – доля студентов, не выполнивших или не справившихся с текущими заданиями. Проблемы и принципы работы с группами иностранных студентов различного уровня подготовленности по математике подробно обсуждаются в работе [3].
Все дисциплины первого семестра, и особенно математические, кроме обеспечения профессиональных компетенций, участвуют в формировании общекультурной компетенции – умение учиться и самоорганизовываться. Данное умение приобретается именно в первые месяцы учебного семестра и используется во всех дальнейших дисциплинах. На рис. 3 представлены результаты средних баллов экзаменационной оценки за 1-ый и 2-ой семестры по выборке студентов за 5 исследуемых лет.
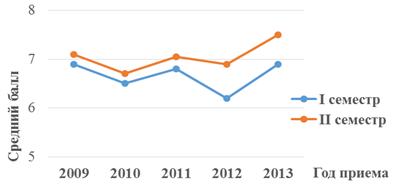
Рис. 3. Средняя итоговая оценка за 1-ый и 2-ой семестры
Нужно отметить, что 1-ый семестр математического анализа включает ряд понятий и тем, с которыми студенты знакомились в школе – предел, производная, исследование функции. То есть студенты уже имеют представление об инструментах анализа, лишь рассматривают их с обобщенных позиций в рамках единой аксиоматики. Проблемой является именно отсутствие умения за короткое время воспринимать и усваивать большие объемы информации, связывать одни понятия с другими, обозревать изучаемый предмет в общем. Второй семестр насыщен незнакомыми, достаточно громоздкими задачами и абстрактными понятиями, базирующимися на темах первого семестра (определенный, несобственный и кратный интеграл, числовой и функциональный ряд и др.). Тем не менее, как видно из рис. 3, наблюдается стабильное повышение экзаменационной оценки второго семестра по сравнению с первым. Это, безусловно, радует, и мы делаем вывод, что на некотором уровне мы справляемся с задачей формирования непростой компетенции «умение учиться».
Подробный статистический анализ средней успеваемости студентов проводится в работе [6]. Мы лишь остановимся на сравнении характеристик связи между оценками, полученными студентами при выполнении различных видов работ. В таблице 3 приведены коэффициенты корреляции между составными частями результирующей оценки: рейтинговым семестровым баллом (как отмечалось выше, 60 % данной оценки составляет результирующую) и баллами, полученными на экзамене (40 % данной оценки составляет результирующую).
Таблица 3
Коэффициенты линейной корреляции между рейтинговой семестровой оценкой и оценкой ответа на экзамене и между оценкой ответа на экзамене и результирующей оценкой
|
|
Рейтинг в семестре и ответ на экзамене |
Ответ на экзамене и результирующая оценка |
||
|
1 семестр |
2 семестр |
1 семестр |
2 семестр |
|
|
2009 |
0.35 |
0.54 |
|
|
|
2010 |
0.38 |
0.52 |
|
|
|
2011 |
0.35 |
0.70 |
0.80 |
0.91 |
|
2012 |
0.60 |
0.40 |
0.85 |
0.86 |
|
2013 |
0.40 |
0.60 |
0.83 |
0.90 |
Как видно из таблицы 3, в годы, когда работа в семестре не учитывалась в экзаменационной оценке (2009 г. и 2010 г.), связь между результатом семестровой работы и оценкой за дисциплину в 1-ом семестре достаточно низкая (коэффициент корреляции меньше 0,4). Во 2-ом семестре корреляция увеличивается до 0,5. Однако после изменения структуры результирующей оценки корреляция между семестровыми баллами и ответом на экзамене увеличивается. Также прослеживается тенденция на улучшение этой связи от семестра к семестру. Причем, если в первом семестре корреляция практически не изменяется на протяжении всего исследуемого периода (исключение – 2012 г.), то во втором – коэффициент корреляции растет при переходе от 2010 года к последующим годам. То же можно сказать и о средней итоговой оценке за первый семестр. Как видно на рис. 3, изменения в оценивании никак не сказались на итоговой оценке 1-го семестра. Колебания мы связываем с различным средним уровнем школьной математической подготовки студентов.
В период принятия новой структуры экзаменационной оценки у преподавателей были сомнения, что учет в итоговой оценке рейтинговых баллов приведет к ухудшению подготовки студентов непосредственно к экзамену. Мы сравнили средний балл за ответ на экзамене: 7.05 в 2011 г., 7.0 в 2012 г. и 7.5 в 2013 г., и результирующий балл: 6,7 в 2011 г., 6.7 в 2012 г. и 7.3 в 2013 г. (второй семестр). В то же время, как видно из таблицы 3, наблюдается сильная корреляция между этими оценками. Среднеквадратические отклонения в рядах изменяется от 1.52 до 1.78. Действительно, такая система формирования итоговой оценки более прозрачна для студента, позволяет до экзамена оценить свои возможности и, при желании, можно «поправить свои дела» хорошим ответом на экзамене.
Заключение. Таким образом, на основании проведенных оценок можно сделать следующие выводы.
1. Результаты входного тестирования удовлетворительно коррелируют с результатами ЕГЭ, но при этом позволяют преподавателю адресно рекомендовать студенту траекторию обучения: элитное образование, традиционное, адаптационное – выравнивающее до традиционного.
2. Сравнительный анализ результатов оценок обучения за первые два семестра и их корреляции позволяют сделать вывод о формировании у студентов общекультурной компетенции «умение учиться и самообучаться».
3. Переход на составную итоговую экзаменационную оценку, состоящую на 60 % из рейтингового семестрового балла и на 40 % из балла за ответ на экзамене, оказался оправданным. Он сыграл мотивационную роль к равномерной работе студентов в течение всего семестра; сгладил разрыв в оценках слабых, но работающих и сильных, но неработающих студентов; позволил студентам на протяжении семестра следить за своими успехами, вовремя корректировать недоработки, осмысленно с ожидаемым заранее результатом готовиться к итоговому экзамену.
Рецензенты:
Килин В.А., д.ф.-м.н., профессор кафедры Высшей математики ФГАОУ ВО «Национальный исследовательский Томский государственный университет», г. Томск;
Рожкова С.В., д.ф.-м.н., профессор кафедры организации и технологии высшего профессионального образования ФГАОУ ВО «Национальный исследовательский Томский политехнический университет», г. Томск.
Библиографическая ссылка
Имас О.Н. ИТОГОВАЯ ОЦЕНКА ПО КУРСУ МАТЕМАТИЧЕСКИЙ АНАЛИЗ: АЛЬТЕРНАТИВНЫЕ ВАРИАНТЫ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18060 (дата обращения: 12.03.2026).



