Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Миненко Д.О. 1

---

1 ФГБОУ ВПО ПГУПС "Петербургский государственный университет путей сообщения Императора Александра I"

Проведен анализ взаимосвязи социально-экономических факторов и пассажиропотока на железнодорожных направлениях, перспективных для сооружения высокоскоростных магистралей. Была выявлена тесная связь между пассажиропотоком железнодорожного и авиационного видами транспорта и такими показателями, как численность населения, населённость гостиниц и валовой региональный продукт на направлениях Москва - Санкт-Петербург, Москва - Казань, Москва - Адлер. В ходе исследований была разработана математическая модель пассажиропотока и определены уравнения множественной линейной регрессии с учетом рассматриваемых социально-экономических факторов для исследуемых направлений. В результате расчета определены доверительные интервалы и область прогноза, а также получены прогнозные значения пассажиропотоков железнодорожного и авиационного транспорта в рассматриваемом железнодорожном полигоне.

Статья в формате PDF

517 KB

высокоскоростная железнодорожная магистраль

анализ

пассажиропоток

1. Алпысова, В.А., Бушуев, Н.С., Миненко Д.О. Моделирование и прогнозирование пассажиропотока высокоскоростной магистрали на примере поездов "Сапсан" направления Санкт-Петербург - Москва / В.А. Алпысова, Н.С. Бушуев, Д.О. Миненко / Транспорта Урала. – 2014. – Вып.2 (41). – С. 50-53.

2. Бендат, Дж. Измерение и анализ случайных процессов / Дж. Бендат, А. Пирсол / Мир, 1971. – 409 с.

3. Вуколов, Э.А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов Statistica и Excel: учебное пособие / Э.А. Вуколов / - 2-е изд. – М., 2014. – 464 с.

4. Данные ОАО Аэропорт «Пулково» [Электронный ресурс]. – Режим доступа: www.pulkovoairport.ru (дата обращения: 20.09.2014).

5. Данные Федерального агентства по туризму (Ростуризм) [Электронный ресурс]. – Режим доступа: www.russiatourism.ru (дата обращения: 10.09.2014).

6. Данные Федеральной службы государственной статистики России (Росстата) [Электронный ресурс]. – Режим доступа: www.sks.ru (дата обращения: 10.09.2014).

7. Дубров, А.М. Многомерные статистические методы: Учебник / А.М. Дубров, В.С. Мхитарян, Л.И. Трошин / М. Финансы и статистика, 2003. – 352 с.

8. Ефимова, М. Р. Практикум по общей теории статистики: учеб. пособие. / М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова / 3-е изд. – М.: Финансы и статистика, 2007. – 368 с.

9. Стратегия развития железнодорожного транспорта в Российской Федерации до 2030 года (новая редакция от 11.06.2014 г.).

Согласно "Стратегии развития железнодорожного транспорта до 2030 года" [9], одним из основных направлений в России сегодня является развитие скоростного и высокоскоростного железнодорожного движения. Предусматривается повышение маршрутных скоростей дальних пассажирских поездов, следующих на расстояния более 700 км, организация скоростного железнодорожного движения со скоростями 200 км/ч, а также строительство выделенных высокоскоростных магистралей со скоростями до 350 км/ч (далее ВСМ). В документе указано, что значительное сокращение времени в пути привлечет на железнодорожный транспорт дополнительный пассажиропоток с авиационного и автомобильного транспорта.

Опыт эксплуатации высокоскоростного железнодорожного транспорта ряда зарубежных стран свидетельствует о том, что экономически эффективный пассажиропоток, приходящийся на ВСМ, не должен быть менее 5-6 млн. чел. в год. Очевидно, что анализ реального прогноза социально-экономического развития агломераций, тяготеющих к ВСМ, и ожидаемая величина пассажиропотока на основных направлениях организации высокоскоростного движения поездов, предусмотренных указанной выше Стратегией остаются основными задачами в области исследований по внедрению высокоскоростных железнодорожных магистралей в России.

Метод исследования пассажиропотока

Важно отметить, что величину пассажиропотока любого вида транспорта на конкретном направлении всегда можно рассчитать, зная график движения, вместимость, процент заполняемости и т.д. Очевидно, что для внедрения нового конкурентоспособного вида транспорта этого недостаточно, т.е. необходим более глубокий анализ развития тяготеющих к ВСМ регионов и городов. Особое внимание следует уделять прогнозу пассажиропотока с учетом влияния на него наиболее значимых социально-экономических факторов, характеризующих рассматриваемый полигон [1].

Согласно [3] существуют две группы методов прогнозирования: интуитивные, основанные на суждениях и оценках экспертов, и формализованные, основанные на математических моделях. Важно отметить что именно формализованные методы позволяют смоделировать процесс изменения пассажиропотока, определив математическую зависимость между исследуемым объектом и характеризующими его признаками. Известно, что все формализованные методы подразделяются на модели предметной области и модели временных рядов. Модели предметной области хорошо известны в термодинамике, механике, медицине. А используемые в этом методе математические модели основаны на существующих законах предметной области и известных дифференциальных уравнениях.

В свою очередь, модели временных рядов описывают зависимость между исследуемыми объектами, и на основе полученной зависимости вычисляются прогнозные показатели. Поскольку исследование перспективного пассажиропотока требует изучения характера изменения некоторого множества факторов, одним из наиболее очевидных методов прогнозирования будет являться регрессионный анализ.

Как отмечается в [3], на основе собранных статистических данных [4, 5, 6] можно определить связь между величиной пассажиропотока и социально-экономическими факторами в полигоне, тяготеющем к ВСМ. Задача сводится к определению множественной регрессионной модели, которая определяется уравнением:

(1.1)

где Y – зависимая переменная (отклик), характеризующая наблюдаемый объект (пассажиропоток); β0, β1, β2, ... , βn – параметры линейной регрессии; X1, X2 ... Xn – независимые переменные (факторы, объясняющие изменение Y); ε – вектор случайных ошибок наблюдений.

Для нахождения оценок параметров по результатам наблюдений используется метод наименьших квадратов. Поскольку анализ множественной регрессии на основе системы уравнений – это трудоемкий процесс, для расчетов используется аппарат матричной алгебры.

Анализ влияния исследуемых социально-экономических факторов на величину пассажиропотока

Рассмотрим три наиболее обсуждаемых сегодня в области сооружения ВСМ железнодорожных направления в России: Санкт-Петербург – Москва, Москва – Казань и Москва – Адлер. Для составления множественной регрессионной модели для каждого направления примем в качестве факторов влияния следующие показатели: данные о численности агломераций (Х1), населённости гостиниц, характеризующие часть туристического потока (Х2) и величины валового регионального продукта, далее ВРП, характеризующие экономическое развитие и деловую активность регионов (Х3) [5, 6].

Предлагается проанализировать как пассажиропоток существующего железнодорожного транспорта, так и пассажиропоток авиасообщения. Согласно источникам статистические данные пассажиропотока железнодорожного и авиационного видов транспорта для маршрута С.-Петербург – Москва взяты за период с 1995 по 2012 годы, для направлений Москва – Казань и Москва – Адлер данные по пассажиропотоку имеются только за период с 2003 по 2012 годы.

C целью установления степени зависимости между рассматриваемыми статистическими данными факторов Х1, Х2 и Х3 и показателями пассажиропотока железнодорожного и авиационного видов транспорта были рассчитаны коэффициенты корреляции в программе MS Excel (см. таблицы 1, 2).

Таблица 1

Коэффициент корреляции для железнодорожного транспорта

Таблица 2

Коэффициент корреляции для авиационного транспорта

Полученные коэффициенты корреляции имеют положительные значения, в основном близкие к единице, что говорит о сильной степени влияния [8] рассматриваемых факторов на величину пассажиропотока железнодорожного и авиационного видов транспорта на всех трех направлениях.

Математическая модель и прогноз пассажиропотока железнодорожного и авиационного видов транспорта

Согласно уравнению (1.1) и набору статистических данных по направлениям спрогнозируем пассажиропоток Y методом оценки множественной регрессии. Общий алгоритм регрессионного анализа [7] для некоторого направления:

1. Составляем матрицу исследуемых факторов – матрицу Х и матрицу данных пассажиропотока – матрицу Y.

2. Проверяем определитель матрицы |ХТ·Х|. Для того, чтобы уравнение регрессии имело решение, определитель матрицы не должен быть равен нулю, т.е. матрица должна являться невырожденной [7].

3. Определяем матричным способом неизвестные коэффициенты уравнения по формуле:

(1.2)

где B – вектор-столбец коэффициентов уравнения регрессии, XT – транспонированная матрица Х, X – матрица размерности n м строк и (k+1) – столбцов известных факторов влияния Х1, Х2 и Х3, Y – вектор-столбец наблюдений размерности n (где n м число наблюдений опыта (период наблюдений для направлений различный; k – количество факторов влияния, равное 3).

4. Записываем полученное уравнение регрессии.

5. Проверяем значимость полученного уравнения регрессии по критерию дисперсионного анализа (F-критерию), а также значимость отдельных коэффициентов регрессии (по критерию Стьюдента).

В ходе исследования было установлено, что на всех направлениях математическая модель не подтверждает значимость полученных коэффициентов регрессии. Была проанализирована корреляционная связь между рассматриваемыми факторами влияния Х1, Х2 и Х3 и получены результаты их тесной связи на всех рассматриваемых направлениях. Согласно [7], в классической линейной регрессионной модели предполагается, что случайные составляющие не коррелируют друг с другом. Однако, существует метод оценки коэффициентов уравнения регрессии взвешенным методом наименьших квадратов. Рассмотрим частный случай.

Пусть матрица Ω является диагональной с элементами известных дисперсий σi2.

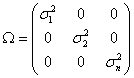(1.3)

Принимаем, что случайные «ошибки» некоррелированы между собой и имеют разные, но известные дисперсии. Если предположить, что относительная ошибка измерения Yi постоянна и равна σ0, то среднеквадратическое отклонение σi будет пропорционально математическому ожиданию ỹi = Myi /x этой величины, т.е. σi = σ0· ỹi.

Далее приступаем к двушаговой процедуре решения данной задачи [7]:

1 шаг: классическим методом наименьших квадратов найдем значения оценок уравнения регрессии Ŷi и определим среднюю относительную ошибку аппроксимации по формуле:

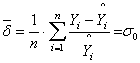(1.4)

2 шаг: предполагая, что оценка среднеквадратического отклонения величины Yi равна ŝi = σ0· Ŷi, найдем матрицу Ω по формуле:

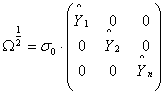(1.5)

Рассчитаем новые коэффициенты уравнения регрессии с учетом матрицы Ω:

(1.6)

Проверяем полученную математическую модель на адекватность и значимость коэффициентов уравнения регрессии. При этом определяем оценку ковариационной матрицы S вектор-столбца B по формуле:

(1.7)

Результаты множественного регрессионного анализа пассажиропотока железнодорожного и авиационного видов транспорта для рассматриваемых направлений сведены в таблицу 3.

Таблица 3

Результаты регрессионного анализа

Важно отметить, что на распределение величины пассажиропотока влияют многие факторы: социальные, экономические, политические и т.д. Характер влияния этих факторов трудно предсказуем. Очевидно, что рассматриваемые статистические показатели пассажиропотока представляют собой сложный процесс случайного характера. Необходимо правильно определить доверительные интервалы прогноза пассажиропотока.

Согласно [2], область высокой корреляции в автокорреляционной функции позволяет анализировать информацию о том, в какой степени значения процесса в некоторый момент времени влияют на значения процесса в некоторый момент в будущем. Что требуется для определения границ прогноза регрессии.

Полученная оценка автокорреляционной функции показала, что для исследуемого диапазона статистических показателей предел прогноза составляет 5 лет, т.е. прогнозные значения пассажиропотоков железнодорожного и авиационного видов транспорта следует определять до 2018 года. Однако, в рамках рассматриваемого документа [9], также будет интересен долгосрочный прогноз пассажиропотока для направлений Санкт-Петербург – Москва, Москва – Казань и Москва – Адлер, что свидетельствует о значительном снижении достоверности полученных прогнозных данных до 2030 года.

В ходе дальнейших исследований и корректировки количества наблюдений прогноз будет уточняться.

Согласно расчету и полученным уравнениям регрессии (таблица 3) спрогнозируем пассажиропоток на направлениях Санкт-Петербург – Москва, Москва – Казань и Москва – Адлер с учетом влияния трёх рассмотренных факторов (см. таблицу 4).

Таблица 4

Показатели суммарного пассажиропотока по направлениям

Заключение

В ходе расчетов исследовано и доказано влияние социально-экономических факторов на изменение и рост пассажиропотока на направлениях Санкт-Петербург – Москва, Москва – Казань и Москва – Адлер. К таким факторам относятся, в частности, численность населения, населенность гостиниц, характеризующая часть туристической массы и валовой региональный продукт. Определено уравнение множественной линейной регрессии с учетом рассматриваемых социально-экономических факторов для прогноза пассажиропотоков железнодорожного и авиационного транспорта направлениях Санкт-Петербург – Москва, Москва – Казань и Москва – Адлер. Рассчитаны доверительные интервалы и область прогноза для уравнений регрессии с помощью регрессионного и автокорреляционного анализа, а также получены прогнозные значения пассажиропотоков железнодорожного и авиационного транспорта.

Рецензенты:

Свинцов Е.С., д.т.н., профессор, профессор кафедры «Изыскания и проектирование железных дорог», ФГБОУ ВПО ПГУПС "Петербургского государственного университета путей сообщения Императора Александра I", г. Санкт-Петербург.

Дудкин Е.П., д.т.н., профессор, профессор кафедры «Строительство дорог транспортного комплекса», ФГБОУ ВПО ПГУПС "Петербургского государственного университета путей сообщения Императора Александра I", г. Санкт-Петербург.

Библиографическая ссылка