В настоящее время приоритетным направлением отечественного домостроения является малоэтажное строительство, особенно актуальным становиться быстро сборные деревянные дома. В связи с этим исследование деревянных строительных конструкций становятся востребованным направлением научных исследований.
Разработка экономичных и долговечных соединений в деревянных конструкциях может существенно снизить материальные издержки при строительстве (жилом или промышленном). Одним из перспективных соединений авторы считают, соединения на вклеенных стальных шайбах обладающие достоинствами других видов соединений, но в тоже время, исключающее многие их недостатки [5, 8]. Данный вид соединений активно используется при строительстве большепролетных зданий и сооружений.
Суть соединений: гнездо под шайбу выбирается слегка увеличенных размеров, что позволяет осуществлять свободную укладку в него металлической шайбы, а образовавшееся «лишнее» пространство в гнезде заполняется полимерной композицией, которую вводят в гнездо перед укладкой шайбы. После отвердения клеевой композиции шайба надежно вклеивается в древесину, что позволяет ей сразу включиться в работу, минуя стадию первоначального обмятия и обжатия [1]. При этом отпадает необходимость в специальных технологических линиях по изготовлению клеевых соединений, кол-во же клеевых полимеров (в расчёте) на одно изделие минимальное, что способствует уменьшению экономических издержек. Более подробно об исследованиях характеристик данного вида соединений представлено в работах [2…6].
В работе [7] была предпринята попытка назначения несущей способности вклеенной шайбы при передаче усилий под углом к волокнам древесины.
Целью данной работы является определение несущей способности вклеенной шайбы при передаче усилий под углом к волокнам древесины, для выработки оптимальных сечений для соединений на вклеенных шайбах.
Для назначения несущей способности ВШ при передаче усилий под углом aо к волокнам древесины соединяемых элементов целесообразно учесть введением понижающего коэффициента ka, как это сделано в СНиП-II-25-80, для подсчета несущей способности ВШ при передаче ей усилия под углом aо к волокнам древесины можно воспользоваться формулой
(1)
Где 
– несущая способность ВШ подсчитанная по формуле (9) работы [7], когда усилие действует вдоль волокон древесины;
ka – понижающий коэффициент, учитывающий угол передачи усилия по отношению к волокнам древесины.
Путем различных преобразований [N] включила в себя формулу (9) работы [7], в которую входят коэффициенты длительной прочности, коэффициенты вероятностной части надежности, т.е. разброс значений несущей способности и коэффициент изменения работы при пластическом и хрупком разрушении. В итоге задача свелась к нахождению коэффициента kα. Данный коэффициент можно найти, воспользовавшись уравнением эмпирической линии регрессии представленной в виде формул:
y=a+b(х-
), (2)
где х= aо,
y= kα =Nαразр/ Nразр (3)
где Nαразр – разрушающая нагрузка под углом aо к волокнам;
Nразр - разрушающая нагрузка вдоль волокон.
Необходимо отметить, что в формуле (3) Nαразр и Nразр, берутся для одних и тех же типоразмеров таких, как Dш, t, толщина, ширина и высота образца которые остаются постоянными, а изменяемым параметром здесь является aо. Величины разрушающих нагрузок под углом aо к волокнам для постоянных параметров (Dш, t, толщина, ширина и высота) приведены в работе [5] и сведены в табл. 1
Таблица 1
Величины разрушающих нагрузок под углом aо к волокнам
|
№ |
Серия |
αо |
Nαi (кН) |
Nαср (кН) |
||||
|
1 |
С′-1 |
0 |
97,9 |
99,3 |
100,3 |
100,8 |
101,2 |
99,9 |
|
2 |
С′-3 |
45 |
96,3 |
96,7 |
97,5 |
97,9 |
98,2 |
97,32 |
|
3 |
С′-4 |
60 |
92,3 |
93,4 |
94,7 |
95,3 |
95,4 |
94,22 |
|
4 |
С′-5 |
90 |
88,8 |
89,6 |
91,5 |
92,4 |
93,3 |
91,12 |
Согласно формулам (2) и (3) таблицу 1 представим в виде таблицы 2.
Таблица 2
Величины разрушающих нагрузок под углом aо к волокнам согласно формулам (2) и (3)
|
i |
αо |
yij |
ni |
|
||||
|
1 |
0 |
0,979 |
0,993 |
1,004 |
1,009 |
1,013 |
5 |
1 |
|
2 |
45 |
0,963 |
0,967 |
0,975 |
0,979 |
0,982 |
5 |
0,974 |
|
3 |
60 |
0,923 |
0,934 |
0,947 |
0,953 |
0,954 |
5 |
0,943 |
|
4 |
90 |
0,888 |
0,896 |
0,915 |
0,924 |
0,933 |
5 |
0,912 |
Вначале проверяется гипотеза об однородности условных дисперсий, все необходимые вычисления сведены в таблицу 3.
Таблица 3
Условные дисперсии
|
i |
ni |
|
(yij- |
S² |
S²li |
||||
|
1 |
5 |
1 |
0,0004008 |
3,607E-05 |
1,6E-05 |
8,12E-05 |
0,000169 |
0,0007034 |
0,0001758 |
|
2 |
5 |
0,9741 |
0,0001042 |
3,851E-05 |
3,25E-06 |
3,37E-05 |
7,76E-05 |
0,0002573 |
6,4328E-05 |
|
3 |
5 |
0,9431 |
0,0003693 |
6,737E-05 |
2,31E-05 |
0,000117 |
0,00014 |
0,0007162 |
0,00017905 |
|
4 |
5 |
0,9121 |
0,0005393 |
0,0002315 |
1,45E-05 |
0,000164 |
0,000476 |
0,0014256 |
0,00035641 |
Проверка гипотезы о равенстве (однородности) эмпирических дисперсий при одинаковых объемах выборок n=5 выполняется с помощью критерия Кочрена по формуле (4) (т.к. одна из дисперсий значительно больше остальных), основанной на выполнении неравенства:
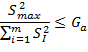(4)
где Ga=0,288 критическое значение критерия Кочрена для уровня статистической значимости α=0,05 и числа серий m=9 и числа степеней свободы K=45-1=44 [8].
Поскольку выполняется неравенство (3)
(5)
то нулевая гипотеза о равенстве генеральных дисперсий не отвергается. В этом случае значения параметров регрессии определяются по формулам [9,10] а вычисления представим в виде таблицы 4. Уравнение эмпирической линии регрессии (при параметрах х=48,75, a=
=0,957, b=0,00099) согласно уравнениям (4) и (5) имеет вид:
y=1,0055-0,0099х (6)
или
kα =1-0,001•αо (7)
Таблица 4
Параметры регрессии
|
i |
ni |
|
Σ (yij- |
yi |
ni*(yij- |
(yij- |
|
1 |
5 |
1 |
0,000703406 |
1,005522856 |
3,05019E-05 |
-0,00552 |
|
2 |
5 |
0,974174174 |
0,000257314 |
0,961062396 |
0,000171919 |
0,013112 |
|
3 |
5 |
0,943143143 |
0,000716232 |
0,946242242 |
9,60442E-06 |
-0,0031 |
|
4 |
5 |
0,912112112 |
0,00142565 |
0,916601935 |
2,01585E-05 |
-0,00449 |
|
Σ |
0,003102602 |
3,829429429 |
0,000232184 |
≈0 |
||
Для проверки линейности полученного уравнения определяeтся осредненная выборочная условная дисперсия по формуле:
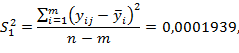(8)
дисперсия вокруг эмпирической линии дисперсии по формуле:
(9)
дисперсное отношение 
. По табл [7,8] для уровня значимости α=0,05 и чисел степеней свободы k2=n-m=20-4=16 и k1=m-2=4-2=2 определяется критическое значение Fα=2,28. Поскольку F<Fα, то наличие линейной зависимости подтверждается. В этом случае дисперсия объединяется в общую оценку по формуле:
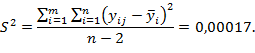(10)
выполняется проверка нулевой гипотезы о наличия зависимости разрушающей нагрузки от параметров шайбы диаметра (Dш) и толщины (t) по [9] определяем t=-10,29. Согласно t и табличным значениям [9,10] для вероятности 0,95 и числа степеней свободы k=n-2=20-2=18 значение tp,k=2,02. Сопоставив вычисленное значение статистики с табличным, можно сделать вывод угол наклона волокон древесины влияет на разрушающую нагрузку (см. рис. 1).
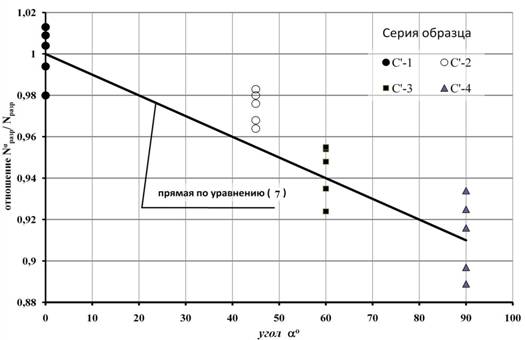
Рис. 1. Зависимости расчетной несущей способности соединений на ВШ от параметров шайб
Если в уравнение (9) работы [1]:
. [1]
подставить уравнение (1) и (7) то получится уравнение:
Nα=(1-10-3•αо)•(6,08+0,784•Dш•t)•Rсм(1+α(��-12)) (11)
где αо – угол передачи усилий относительно волокон древесины;
Dш – диаметр шайбы;
T – толщина шайбы;
R – нормативное сопротивление сортной древесины (МПа);
α – нормативный коэффициент на изменение влажности;
ω– влажность древесины в (в пределах 8-23%).
Данное уравнение, достаточно хорошо отражающие результаты в зависимости от диаметра (Dш) и толщины (t) , а также учитывающие температурно-влажностные параметры, сорт древесины и передачу усилий под углом aо к волокнам.
Рецензенты:
Ласьков Н.Н., д.т.н., профессор, заведующий кафедрой «Строительные конструкции» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;
Логанина В.И., д.т.н., профессор, заведующий кафедрой «Управление качеством и технологии строительного производства», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Библиографическая ссылка
Арискин М.В., Дмитриева Н.Е., Гарькин И.Н. НАЗНАЧЕНИЕ ПРЕДЕЛЬНОЙ НЕСУЩЕЙ СПОСОБНОСТИ ВКЛЕЕННОЙ ШАЙБЫ ПРИ ПЕРЕДАЧЕ УСИЛИЙ ПОД УГЛОМ К ВОЛОКНАМ ДРЕВЕСИНЫ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18014 (дата обращения: 20.04.2024).