Рост рынков сбыта и отдельных отраслей промышленности современной экономики, появление новых предприятий и компаний, расширение торговых сетей делает актуальной задачу автоматизации процессов поиска и привлечения кадров [6]. Особенностью рассматриваемой предметной области является использование совокупности количественных и качественных критериев при выборе претендента на ту или иную должность. Строгая точность одной группы критериев и размытые оценки другой группы могут привести к потере части наилучших претендентов или неправильному их ранжированию [4]. В связи с этим при создании автоматизированных систем подбора персонала возникает необходимость использования все более гибких методов, позволяющих формализовать процесс принятия решений в условиях снижения неопределённости первой группы количественных критериев и «смягчения точности» качественных критериев.
Цель
Повысить качество отбора персонала в условиях как неопределенности, так и излишней точности, призвана предлагаемая авторами методика представления знаний, положенная в основу автоматизированной системы подбора персонала и использующая нечёткие экспертные оценки и нечёткие способы их обработки.
Материалы и методы исследования
Существенным отличием методов теории нечётких множеств от классических методов многокритериального анализа, заключается в том, что и количественные, и качественные критерии приводятся в область нечёткого представления и обрабатываются методами преобразования нечётких величин. Это позволяет существенно повысить достоверность выводов и принимаемых решений. Справедливости ради следует отметить, что такой подход в различных вариациях широко используется в экономике, социальной и управленческой сферах [1, 2], а в последнее время – и в технических системах [3].
База знаний (БЗ) рассматриваемой системы подбора персонала первоначально заполнена сведениями о должностях, на которые производится отбор персонала, и перечнем минимально необходимых квалификационных требований к претендентам. Эти требования являются критериями выбора Cj. Каждой должности соответствует свой набор критериев, которые предварительно ранжированы по степени значимости (важности) применительно к этой должности. Кроме того, каждому критерию соответствует своя лингвистическая шкала, содержащая нечётко выраженные степени (уровни, термы), требующие не количественно заданных интервалов, а субъективную оценку на естественном языке. Например, критерий «стаж работы» может иметь следующую шкалу оценки: {«недостаточный», «минимально-необходимый», «достаточный», «более чем достаточный»}; критерию «уровень образования» может соответствовать шкала {«начальный», «средний», «выше среднего», «высокий», «очень высокий»}. Причём в последнем случае периферийный вуз, по мнению эксперта, может иметь невысокий уровень, а столичный колледж – весьма высокий. Число уровней лингвистической шкалы может варьироваться от критерия к критерию и изменяться от двух до десяти – больше, по мнению авторов, задавать не стоит. Примеры шкал: двузначная {«неприемлемый», «приемлемый»}; пятизначная {«очень низкий», «низкий», «средний», «высокий», «очень высокий»}; десятизначная {«недопустимый», «очень плохой», «плохой», «существенно хуже обычного», «незначительно хуже обычного», «обычный», «незначительно лучше обычного», «существенно лучше обычного», «достаточно хороший», «очень хороший»}. Так как критерии могут выражаться не только в двусторонних отклонениях от среднего значения, но и в односторонних, то могут иметь место шкалы вида: {«абсолютно хуже нормы», «существенно хуже нормы», «незначительно хуже нормы», «в пределах нормы»}. Использование данных шкал позволяет полностью перекрыть потребности экспертов в выборе лингвистических значений критериев при оценивании каждой альтернативы.
Согласно терминологии теории нечётких множеств критерий Cj представляет собой лингвистическую переменную, множество значений которой сi соответствует множеству термов лингвистической шкалы. Каждый терм представляет собой нечеткую переменную, заданную на универсальном множестве U с функцией принадлежности ![]() , причем для термов можно рассматривать те же характеристики, что и для нечетких множеств [5].
, причем для термов можно рассматривать те же характеристики, что и для нечетких множеств [5].
Переход от лингвистических оценок, выставленных экспертом в процессе рассмотрения каждой альтернативы, к соответствующим числовым значениям, которые будут использоваться при последующих расчётах, осуществляется на основе следующих положений:
1) для всех критериев предлагается единый универсальный диапазон U = [0; 1]; нулевое значение соответствует наихудшей оценке, единичное – наилучшей; числовые критерии с иными диапазонами значений приводятся к указанному интервалу;
2) функции принадлежности термов лингвистической переменной являются функциями треугольного вида; супремумы функций ![]() в дальнейшем будут использоваться как значения нечётких чисел, отражающие субъективную степень уверенности эксперта при оценке претендента по критерию Cj;
в дальнейшем будут использоваться как значения нечётких чисел, отражающие субъективную степень уверенности эксперта при оценке претендента по критерию Cj;
3) число перекрывающихся интервалов Nint универсального единичного множества равно числу термов лингвистической шкалы. Крайним термам соответствуют числовые значения – 0 и 1; центральным термам – вещественные значения середины соответствующего интервала.
Ширину интервала можно определить по-разному: 1) установить равные по длине интервалы (вариант 1 в табл. 1 и на рис. 1.1); 2) установить широкий центральный интервал с уменьшением к краям диапазона (вариант 2); 3) установить ширину интервалов, таким образом, чтобы она увеличивалась к краям так, что отношение длин соседних интервалов стремилось к золотому сечению (вариант 3); 4) то же, что и вариант 3, только ширина интервалов уменьшается от центра к краям (вариант 4). Варианты 3 и 4 удобны в случае, когда основная часть оценок соответственно сосредоточена в центре или по краям диапазона. Варианты 1 и 2 имеют более универсальный характер.
Таблица 1
Границы термов для пятизначной лингвистической шкалы
|
Вариант |
1 |
2 |
3 |
4 |
5 |
|
очень низкий |
низкий |
средний |
высокий |
очень высокий |
|
|
1) |
0 : 0,25 |
0 : 0,50 |
0,25 : 0,75 |
0,50 : 1,00 |
0,75 : 1,00 |
|
2) |
0 : 0,125 |
0 : 0,50 |
0,125 : 0,875 |
0,50 : 1,00 |
0,875 : 1,00 |
|
3) |
0 : 0,445 |
0,275:0,50 |
0,445:0,555 |
0,50 : 0,725 |
0,555 : 1,00 |
|
4) |
0 : 0,12 |
0,12 : 0,50 |
0,12 : 0,88 |
0,5 : 1,00 |
0,88 : 1,00 |
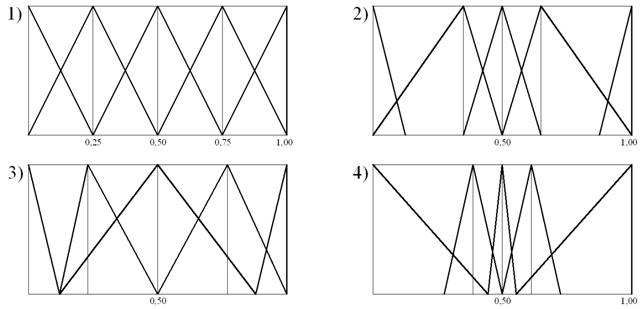
Рис. 1. Графическое представление термов пятизначной шкалы по вариантам таблицы 1.
Выбор способа оцифровки значений нечётких переменных осуществляется в настройках системы подбора персонала. По умолчанию используется первый вариант. Эксперт может изменить вариант соотношения длин интервалов как для всех критериев сразу, так и для каждого в отдельности.
Система может принимать решение по выбору кандидатов на основе базового набора с привлечением одного лица, принимающего решение (ЛПР) о соответствии претендента на должность. При необходимости к процессу выбора могут привлекаться эксперты, каждый из которых может: 1) изменять порядок ранжирования базовых критериев, вплоть до исключения некоторых из них из процесса принятия решения; 2) добавлять дополнительные критерии, которые будут учитываться наряду с базовым набором; 3) определять ранг новых критериев и формировать для каждого из них лингвистическую шкалу; 4) принимать или отвергать предложения коллег по расширению набора критериев; 5) изменять лингвистические шкалы базовых критериев и критериев, предложенных коллегами. Многопользовательская распределённая архитектура системы на основе «классной доски» позволяет экспертам проводить оперативный обмен предложениями по редактированию набора критериев. Таким образом, каждый эксперт может создать свою собственную систему оценки, включающую набор проранжированных им критериев со своими множествами возможных значений. Для представления знаний в рассматриваемой системе принято решение отказаться от универсальной лингвистической шкалы, дав возможность каждому эксперту самостоятельно определять индивидуальные шкалы.
При выборе способа локального ранжирования критериев решено было остановиться на методе ранжирования, который заключается в следующем. Эксперт упорядочивает все выбранные им критерии по возрастанию их относительной значимости. При этом два и более критерия могут, по мнению эксперта, быть одинаково значимыми. Такие критерии объединяются в группы, но нумеруются последовательно и в произвольном порядке. Ранг критерия определяется его номером, если в своей группе он был единственным; в противном случае ранги равнозначных критериев равны среднему арифметическому их номеров. Наиболее значимому критерию соответствует наименьшее значение ранга. После процедуры распределения критериев их ранги нормируются. В таблице 2 приведен пример ранжирования пяти критериев тремя экспертами.
Таблица 2
Примеры ранжирования для пяти критериев
|
|
Критерии |
С1 |
С2 |
С3 |
С4 |
С5 |
|
|
|
Эксперт 1 |
Ранг (R) |
1 |
2 |
3 |
4 |
5 |
Σ=15 |
|
|
Нормированное значение ранга(r) |
0,067 |
0,133 |
0,200 |
0,267 |
0,333 |
Σ=1 |
||
|
Эксперт 2 |
Критерии |
С1, С2 |
С3 |
С4, С5 |
|
|||
|
Ранг (R) |
1,5 |
1,5 |
3 |
4,5 |
4,5 |
Σ=15 |
||
|
Нормированное значение ранга(r) |
0,1 |
0,1 |
0,2 |
0,3 |
0,3 |
Σ=1 |
||
|
Эксперт 3 |
Критерии |
С1, С2, С5 |
С3, С4 |
|
||||
|
Ранг (R) |
2,0 |
2,0 |
2,0 |
4,5 |
4,5 |
Σ=15 |
||
|
Нормированное значение ранга(r) |
0,133 |
0,133 |
0,133 |
0,3 |
0,3 |
Σ=1 |
||
После предварительной настройки множества критериев каждым экспертом система получает в общем случае уникальные множества субъективно проранжированных критериев. Число этих множеств будет равно числу экспертов Nexp, увеличенному на единицу, где +1 соответствует базовому множеству критериев из БЗ. Итоговое множество будет получено в результате пересечения локальных множеств. Порядок ранжирования элементов в итоговом множестве будет зависеть от количества вхождений каждого критерия в исходные множества и значений его рангов в этих множествах, что позволит учесть мнение каждого эксперта.
Предлагаемый авторами алгоритм ранжирования совокупного множества критериев предусматривает: 1) однократное включение критериев в итоговое множество; 2) нормирование локальных рангов каждого критерия; 3) вычисление их среднего значения; 4) нормирование средних значений; 5) умножение пронормированных средних значений рангов на величину, обратную числу вхождений критерия в локальные множества. После указанной процедуры будут получены величины рангов, отражающие относительную ценность каждого критерия. Наименьшие из них позволяют значительно повысить совокупную нечёткую оценку критерия, наибольшие – оставить значение оценки практически без изменений.
Например, при наличии трёх альтернатив четыре эксперта предложили в сумме шесть критериев оценки, расположив их по убыванию значимости. Число выбранных критериев и сами критерии у каждого эксперта свои. Причём первый эксперт считает, что критерии C2 и C3 равнозначны, а последний эксперт равнозначными считает критерии C1 и C2 (табл. 3). Результаты ранжирования критериев совокупного множества согласно предложенному алгоритму представлены в таблице 4.
Таблица 3
Выбор и упорядочение критериев
|
exp1 |
C1(1), |
C2(2), C3(3) |
С6(4) |
|
|
exp2 |
C1(1) |
C2(2) |
C3(3) |
C4(4) |
|
exp3 |
C1(1) |
C2(2) |
C3(3) |
C5(4) |
|
exp4 |
C6(1), |
C1(2), C2(3) |
|
|
Таблица 4
Результаты ранжирования критериев совокупного множества
|
Локальные ранги критериев (R) |
Нормированные значения рангов (r) |
|||||||||||
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
Σ |
Cнорм1 |
Cнорм2 |
Cнорм3 |
Cнорм4 |
Cнорм5 |
Cнорм6 |
|
1 |
2,5 |
2,5 |
|
|
4 |
10 |
0,1 |
0,25 |
0,25 |
|
|
0,4 |
|
1 |
2 |
3 |
4 |
|
|
10 |
0,1 |
0,2 |
0,3 |
0,4 |
|
|
|
1 |
2 |
3 |
|
4 |
|
10 |
0,1 |
0,2 |
0,3 |
|
0,4 |
|
|
2,5 |
2,5 |
|
|
|
1 |
6 |
0,417 |
0,417 |
|
|
|
0,167 |
|
Среднее значение рангов критерия |
0,179 |
0,267 |
0,283 |
0,400 |
0,400 |
0,283 |
||||||
|
Нормирование средних значений |
0,448 |
0,667 |
0,708 |
1,00 |
1,00 |
0,708 |
||||||
|
Количество использований критерия |
4 |
4 |
3 |
1 |
1 |
2 |
||||||
|
Итоговое значение ранга критерия (α) |
0,112 |
0,167 |
0,236 |
1,00 |
1,00 |
0,354 |
||||||
В итоге сформирована генеральная совокупность критериев для конкретной должности, состоящая из шести элементов с соответствующим значением ранга:
С* = {С10.112, С20.167, С30.236, С41.0, С51.0, С60.354}.
В процессе непосредственного общения с претендентами на должность эксперты могут в режиме online: 1) получать анкетные данные, непосредственно влияющие на значение того или иного критерия; 2) производить оценку каждого критерия путём выбора значений из соответствующей ему лингвистической шкалы; 3) выбирать вариант оценки «затрудняюсь ответить», исключая тем самым какой-либо критерий из рассмотрения для конкретного претендента «на лету».
Рассмотрим математическую постановку задачи принятия решения (ЗПР) при наличии одного эксперта. Пусть имеется:
1. Множество альтернатив А = {а1, а2, ...,ai, …, аNalt}; каждый элемент ai соответствует претенденту на должность; число таких альтернатив равно Nalt.
2. Множество критериев С= {С1, С2, ...,Cj,..., СNcrit}; каждый элемент Сj. определяет некоторое свойство претендента. Количество критериев Ncrit определяется одним экспертом и является постоянной величиной. Каждый критерий имеет свою степень значимости (ранг) rj и свою шкалу лингвистических оценок sclj:
![]()
1. Экспертные оценки альтернатив по каждому j-му критерию:

Совокупность оценок, выставленная экспертом для каждой i-ой альтернативы может рассматриваться как нечёткое множество Dj, элементами которого выступают нечеткие числа cj,i, отражающие субъективную степень уверенности эксперта в обладании аi свойством Cj:
Di= { cj,1 /ai, cj,2 /ai, ..., cj,i /ai, ..., cj,Ncrit /ai}.
Правило выбора лучшей альтернативы а* можно осуществить на основе построения нечёткого множества G как пересечение нечетких множеств Di. Операция пересечения нечетких множеств соответствует выбору минимального значения для i-ой альтернативы. Оптимальной считается альтернатива с максимальным значением функции принадлежности множеству G:
G = D1 ∩ D2 ∩ ... ∩ DNcrit ;
![]() .
.
Поскольку критерии Сj имеют различную важность, то их вклад в общее решение можно представить как взвешенное (возведённое в степень rj) значение соответствующего терма:
Di= { (cj,1)r1 /ai, (cj,2)r2 /ai, ..., (cj,i)rj /ai, ..., (cj,Ncrit)rNcrit /ai},
где ri – пронормированные ранги соответствующих критериев, удовлетворяющие следующим условиям:
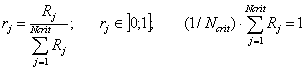 .
.
Определяя нижнюю границу для значений mG, можно отобрать группу претендентов, отвечающих квалификационным требованиям. Далее рассмотрим математическую постановку ЗПР при наличии нескольких экспертов Nexp. Пусть имеется:
1. То же множество исходных альтернатив А = {а1, а2, ..., аNalt}.
2. Каждый эксперт имеет свой набор критериев С(exp)= {С1(exp), С2(exp),..., Сj(exp), ... , СNcrit(exp1)}, отличающийся по составу и способу ранжирования от наборов других экспертов.
3. Совокупное множество критериев С* системы состоит из пересечения указанных наборов и содержит N*crit критериев. Степень повторяемости критериев в каждом локальном наборе представлено множеством целых чисел S = {s1, s2, ..., sN*crit}. Ранжирование критериев осуществлено по описанному выше алгоритму ранжирования множества критериев.
4. Каждая альтернатива имеет переменное число (от 1 до Nexp) лингвистических оценок по N*crit критериям из совокупного множества С*. Лингвистические оценки выражены нечёткими числами di,j на единичном множестве U=[0; 1] со своими функциями принадлежности треугольного вида:
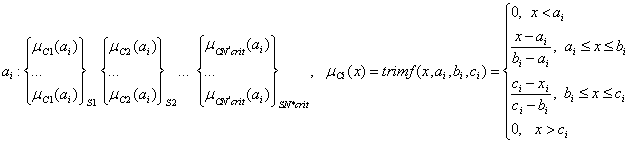
или
![]()
Каждая оценка имеет свой локальный ранг ri и число градаций своей собственной лингвистической шкалы scli.
Первым этапом обработки экспертных данных является получение интегральных (или точечных) оценок по каждому критерию в том случае, если степень повторяемости критерия >1, т.е. критерий выбран двумя и более экспертами. Другими словами, необходимо осуществить преобразование:
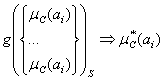 или
или ![]()
Функция свёртки критериев g должна гарантированно возвращать значения на отрезке [0; 1] при любых допустимых значениях оценок, их приоритетов и размера шкалы. Будем рассматривать аргументы функции с позиций нечётких чисел d. Тогда интегральная оценка – нечёткое число d* – может быть получена в результате линейной комбинации нечетких чисел dj и также будет иметь функцию принадлежности треугольного вида. В качестве линейной комбинации могут использоваться коммутативные операции сложения или умножения нечётких чисел. Причём для выполнения условия d*∈[0; 1] сложение потребует учёта локального ранга r и, косвенно, числа градаций лингвистической шкалы scl для каждой нечёткой переменной. Для нечётких чисел, полученных в результате умножения, локальные ранги для возведения в степень не используются, а над результатом умножения впоследствии будет произведена операция возведения в степень α, где α – итоговое значение ранга для каждого критерия. Это позволит «сместить» близкий к нулю результат мультипликативной свёртки в сторону увеличения с учётом частоты использования критерия. Вершина b и границы a и c функции принадлежности нечеткого числа, полученного в результате операций сложения и умножения нечётких чисел (a1,b1,c1) и (a2,b2,c2), вычисляются следующим образом:
a=a1 × a2; c = c1 × c2; b=b1 × b2; где × – обобщённый символ операции.
Аддитивная свёртка имеет преимущество в том случае, когда малое значение оценки по одному из критериев компенсируется большим значением по какому-либо другому или нескольким критериям. Мультипликативная свёртка удачна, когда отсутствуют низкие оценки по критериям, поскольку даже единственный нулевой сомножитель обеспечит нулевой результат. В настройках системы по умолчанию установлена аддитивная свёртка для всех интегральных оценок. Изменение опции доступно только для ЛПР. При установленной мультипликативной свёртке система проверяет наличие нулевых значений нечётких чисел и их правых границ и выдаёт соответствующее предупреждение.
Для вышеуказанного примера (три альтернативы; четыре эксперта; шесть критериев оценки) имеем следующие наборы экспертных оценок для каждой альтернативы:
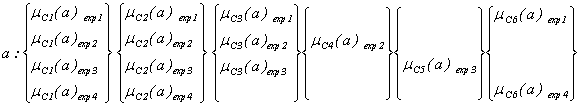
Степени повторяемости критериев, входящие во множество S, таковы:
S = {4, 4, 3, 1, 1, 2}.
Рассмотрим оба варианта свёртки на примере критерия С1. Пусть имеются оценки четырёх экспертов со следующими значениями треугольной функции принадлежности для пятизначной шкалы с неравномерной шириной интервала:

Для оценки важности критериев используются локальные и итоговый ранги, полученные в таблице 4 (столбец 1). В таблицах 5 и 6 приведены примеры аддитивной и мультипликативной свертки экспертных оценок, а на рисунке 2 представлены соответствующие треугольные функции принадлежности исходных оценок (а), интегральной аддитивной оценки (б), интегральной мультипликативной оценки (в).
Таблица 5
Аддитивная свёртка
|
Оценки эксперта |
Значения треугольной функции принадлежности |
||
|
левое |
центральное |
правое |
|
|
ВЫСОКИЙ |
0,500.1 |
0,650.1 |
1,000.1 |
|
ОЧЕНЬ ВЫСОКИЙ |
0,8750.1 |
1,000.1 |
1,000.1 |
|
СРЕДНИЙ |
0,1250.1 |
0,500.1 |
0,8750.1 |
|
СРЕДНИЙ |
0,1250.417 |
0,500.417 |
0,8750.417 |
|
Интегральная оценка |
0,202 |
0,424 |
0,652 |
Таблица 6. Мультипликативная свёртка
|
Оценки эксперта |
Значения треугольной функции принадлежности |
||
|
левое |
центральное |
правое |
|
|
ВЫСОКИЙ |
0,50 |
0,65 |
1,00 |
|
ОЧЕНЬ ВЫСОКИЙ |
0,875 |
1,00 |
1,00 |
|
СРЕДНИЙ |
0,125 |
0,50 |
0,875 |
|
СРЕДНИЙ |
0,125 |
0,50 |
0,875 |
|
Произведение |
0.0070.112 |
0.1630.112 |
0.7660.112 |
|
Интегральная оценка |
0,572 |
0,816 |
0,971 |
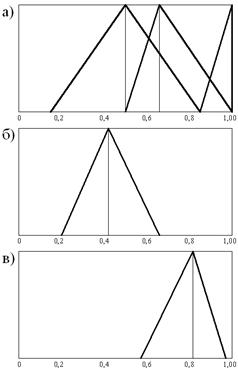
Рис. 2. Функции принадлежности исходных (а) и результирующих (б,в) оценок
Аналогичные интегральные оценки должны быть получены по всем множествам критериев, число элементов в которых больше одного.
После получения интегральных оценок, ЗПР решается на основе метода с единственным экспертом.
Заключение
Предложенная нечёткая система представления знаний и способов их обработки, оперирующая классическими решающими правилами многокритериального выбора на основе нечёткой входной информации, имеет ряд особенностей. К ним относятся:
- возможность обработки с единых позиций как количественных, так и качественных параметров альтернатив;
- организация экспертного опроса с последующим формированием индивидуального набора критериев, их лингвистических шкал и способов ранжирования;
- унификация лингвистической информации на основе гибкой системы задания границ интервалов;
- формирование групповой совокупности критериев и их ранжирование с учётом локальной значимости и частоты использования;
- расширенный механизм получения интегральных оценок по многократно выбранным критериям.
Рассмотренный подход к представлению знаний и способу их обработки позволяет решать задачи выбора персонала как для рабочих и технических специальностей, так и для оценки должностей менеджеров, руководителей, представителей креативных профессий и пр. Кроме того, он может быть использован, например, для оценки уже имеющегося персонала, формирования управленческого резерва, или для формирования группы под определённый проект. Развитие нечёткой модели знаний может идти в направлении поддержки переговорных процессов, где требуются формализованные процедуры согласования, позволяющие осуществить поиск приемлемого компромисса.
Рецензенты:
Арженовский С.В., д.э.н., профессор, профессор кафедры математической статистики, эконометрики и актуарных расчетов ФГОУ ВПО «Ростовский государственный экономический университет (РИНХ)» Министерства образования и науки РФ, г. Ростов-на-Дону;
Ковалёв О.Ф., д.т.н., профессор, профессор кафедры «Информационная безопасность, телекоммуникационные системы и информатика» ФГБОУ ВПО «Южно-Российский политехнический университет (Новочеркасский политехнический институт) имени М.И. Платова», г. Новочеркасск.
Библиографическая ссылка
Георгица И.В., Кузнецова А.В. ПРЕДСТАВЛЕНИЕ ЗНАНИЙ ДЛЯ СИСТЕМЫ ПОДБОРА ПЕРСОНАЛА НА ОСНОВЕ НЕЧЕТКОЙ ЛОГИКИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18012 (дата обращения: 12.03.2026).



