Для построения полной модели адаптивной системы передачи энергии и информации (рис. 1) необходимо создание моделей трассы распространения и исполнительного элемента, выбор которого определяется используемым методом коррекции искажений. В алгоритме обращения волнового фронта (ОВФ) такими элементами могут быть нелинейный кристалл (ОВФ-зеркало) [4] или два упругих зеркала, разделенных промежутком неискажающей среды [9]. При фазовом управлении пучком активных элементов обычно является упругое зеркало. Управление активным элементом осуществляется на основе информации об искажениях пучка на трассе распространения, поступающей из цепи обратной связи. Вид цепи и входящие в нее элементы определяются методом управления (амплитудно-фазовое или чисто фазовое) и алгоритмом коррекции.
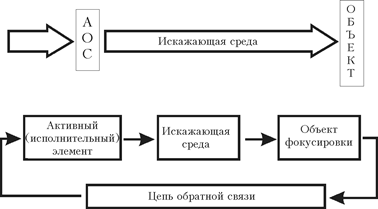
Рис. 1. Структура адаптивной системы, предназначенной для коррекции атмосферных искажений излучения
В алгоритмах обращения волнового фронта и фазового сопряжения [1] информацию об искажениях переносит опорный пучок, распространяющийся навстречу корректируемому пучку. Наибольшая точность достигается, если трассы «прямого» и опорного пучков совпадают, а временная задержка отсутствует.
Таким образом, при численном исследовании работы адаптивной системы необходимым является построение модели трассы распространения излучения, устройства регистрации фазы и корректора волнового фронта. Математические модели перечисленных элементов и описание программной реализации полной модели адаптивной системы приводится в настоящей статье.
Модель распространения оптического излучения в искажающей среде: турбулентность и тепловое самовоздействие
В приближении квазиоптики распространение гауссовского пучка (модель строилась для этого типа излучения) с комплексной амплитудой E(x,y,z,t) в случайно-неоднородной слабопоглощающей среде может быть описано дифференциальным уравнением вида [3]:
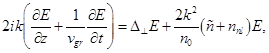 (1)
(1)
где x, y – координаты в плоскости, перпендикулярной направлению распространения пучка; z – координата в направлении распространения; ![]() – оператор Лапласа;
– оператор Лапласа; ![]() – групповая скорость;
– групповая скорость; ![]() – случайное поле флуктуаций показателя преломления, обусловленных турбулентностью;
– случайное поле флуктуаций показателя преломления, обусловленных турбулентностью; ![]() – поле изменений показателя преломления, появление которого вызвано нагревом среды излучением.
– поле изменений показателя преломления, появление которого вызвано нагревом среды излучением.
Для учета теплового самовоздействия (учета изменения показателя преломления за счет нагрева среды пучком) уравнение (1) дополняется материальным уравнением [3]:
![]() . (2)
. (2)
Здесь k – коэффициент теплопроводности; ρ – плотность; Cp – удельная теплоемкость; V – скорость движения среды. Если среда регулярна (нет турбулентных искажений), в сопровождающей системе координат (z¢ = z, t¢ = t – z/vgr, в результирующих уравнениях штрихи опущены) система уравнений (1), (2) может быть переписана как
![]()
![]() (3)
(3)
где k – волновое число; n0 – невозмущенное значение показателя преломления; α - коэффициент поглощения. Совместное решение уравнений, входящих в систему (3), выполняется численными методами на основе алгоритма расщепления по физическим факторам.
Нелинейные искажения излучения определяются безразмерным параметром, называемым обычно параметром нелинейности [2]:
![]()
В приведенной формуле I0 – плотность мощности на оси пучка в плоскости апертуры источника; a0 – начальный радиус пучка; V – скорость потока среды.
Следующим искажающим фактором, учет которого выполнялся в данной работе, являлась атмосферная турбулентность. Математическое задание турбулентных искажений и принципы их численного моделирования достаточно хорошо известны [5], поэтому ниже приводится только краткое описание используемой модели.
Для описания турбулентности А.Н. Колмогоровым была введена структурная функция показателя преломления
![]()
В пределах инерционного интервала (в диапазоне пространственных размеров от внутреннего l0 до внешнего L0 масштаба турбулентности) структурная функция подчиняется закону двух третей:
![]()
где ![]() – структурная характеристика поля показателя преломления (структурная постоянная).
– структурная характеристика поля показателя преломления (структурная постоянная).
Модель адаптивного зеркала с непрерывной отражающей поверхностью
Модели зеркал, приводимые в настоящем разделе, были построены на основе методики, разработанной С.С. Чесноковым [8]. Автором полагалось, что адаптивное зеркало, форма поверхности которого задается системой актюаторов, может быть представлено как тонкая пластина, деформируемая силами, приложенными в дискретных точках. Модель пластины была создана на основе метода конечных элементов, описание которого помещено в монографии [6]. Нами выполнено развитие статической модели. В частности, число приводов было вначале увеличено до 8–20 (рис. 2) и проведен анализ эффективности компенсации теплового самовоздействия. В дальнейшем были значительно смещены ограничения на число степеней свободы зеркала, полное количество актюаторов резко возросло и управление моделью осуществлялось уже в 250 точках.

Рис. 2. Модель зеркала, управляемого системой актюаторов (приложение сил в дискретных точках)
В приближении тонкой однородной изотропной пластины статический прогиб W(x, y) зеркала описывается уравнением бигармонического типа [7]:
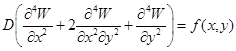 . (4)
. (4)
Здесь x, y – координаты в плоскости пластины; ![]() – цилиндрическая жесткость;
– цилиндрическая жесткость; ![]() – коэффициент Пуассона; E – модуль Юнга; h – толщина пластины; f – поперечная распределенная нагрузка.
– коэффициент Пуассона; E – модуль Юнга; h – толщина пластины; f – поперечная распределенная нагрузка.
Если пластина нагружена системой поперечных сосредоточенных сил Pj, действующих внутри контура, правая часть уравнения может быть представлена в виде
![]()
где xj, yj – координаты актюатора; Sj – его площадь; v – общее число приводов (каналов управления).
Аналитическое решение уравнения (4) и учет граничных условий представляют значительные трудности, поэтому используемые нами модели были построены на основе метода конечных элементов [6].
Описание модели датчика Гартмана
В реальных системах адаптивной оптики для регистрации фазы пучков обычно используется датчик Гартмана [10]. Датчик состоит из набора микролинз (растр), вставленных в оправу, или прозрачной пластины, сформированной из нескольких линз. Массив микролинз фокусирует падающее на прибор излучение. В плоскости регистрации датчика обычно устанавливается видеокамера высокого разрешения или матрица светочувствительных элементов, разделенная на площадки, каждая из которых соответствует одной из субапертур. В пределах площадки регистрируется смещение энергетического центра тяжести пучка, по этому смещению вычисляется локальный (в пределах субапертуры) наклон волнового фронта. На основе метода наименьших квадратов по локальным наклонам восстанавливается фазовая поверхность излучения, поступившего на датчик.
Программная реализация модели адаптивной системы
Как это следует из предыдущих разделов настоящей статьи, полная модель адаптивной системы должна включать модели оптического тракта, зеркала, датчика и, возможно, других элементов. В свою очередь, каждая из перечисленных моделей может быть реализована программно только в виде достаточно сложного блока. Поэтому для создания полной модели нами использовалась одна из методик современного программирования – Component Object Model. С помощью COM вся модель разбивалась на отдельные независимые модули, являющиеся серверами основного приложения. Задавая связи между клиентом и серверами, строили сложное распределенное приложение.
Для выделения из набора объектов, находящихся на компьютере, программа-сервер обладает идентификатором, 128-битовым номером, записываемым в реестр Windows. С его помощью клиент инициализирует сервер и получает указатель на него. Предоставление своих функциональных возможностей клиент осуществляет через интерфейс, состоящий из группы методов, т.е. из набора функций с заданными параметрами. Получив указатель, программа-клиент имеет доступ ко всем методам интерфейса, может передавать и получать параметры, а значит, во многом определяет работу сервера.
В построенном нами распределенном приложении «адаптивная оптическая система» клиентом являлась программа, моделирующая распространение пучка в нелинейной или турбулентной среде. Приложение включало следующие серверы: модель датчика Гартмана, модель зеркала, блок вычисления матрицы жесткости и дополнительно два блока вычисления дислокаций, реализующих два различных алгоритма определения особых точек.
Для алгоритма фазового сопряжения структура приложения приводится на рис. 3.
Полученные массивы (мнимая и действительная части амплитуды) через интерфейс автоматизации IDispatch (еще одна особенность COM, облегчающая программирование) передаются в программу «датчик Гартмана». Используя методы интерфейса, клиент обращается к таким функциям сервера, как деление пучка субапертурами, распространение от линзлета к плоскости регистрации, вычисление положений центров тяжести в пределах субапертур, и, наконец, к функции восстановления фазовой поверхности. Таким образом, клиент полностью управляет сервером.
Восстановленная датчиком фаза передается в программу, моделирующую гибкое зеркало, где выполняется фазовое сопряжение и определяется результирующая форма отражающей поверхности. Вычисление деформаций зеркала выполняется с использованием матрицы жесткости, получение которой вынесено в отдельный блок. После выполнения этих операций массив, характеризующий форму зеркала, возвращается в основную программу (клиент), в которой вновь решается задача распространения, но уже с начальным фазовым профилем пучка, заданным зеркалом.
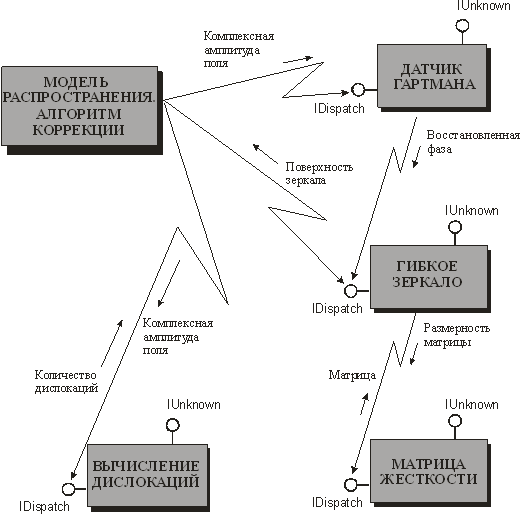
Рис. 3. Структура распределенного приложения, моделирующего адаптивную систему передачи энергии (компенсация искажений на основе фазового сопряжения)
Заключение
В статье приводится описание математической модели адаптивной оптической системы, предназначенной для компенсации тепловых и турбулентных искажений лазерного излучения. Также в статье представлена программная реализация модели, выполненная в виде распределенного программного приложения. Модель может быть использована при численных исследованиях работы реальных оптических систем. Кроме этого, на ее основе может быть разработана лабораторная работа, входящая в учебный курс «Оптика».
Рецензенты:
Исаев Ю.Н., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН НИ ТПУ, Национальный исследовательский Томский политехнический университет, г. Томск;
Новиков С.А., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН НИ ТПУ, Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Канев Ф.Ю., Макенова Н.А. ЧИСЛЕННАЯ МОДЕЛЬ АДАПТИВНОЙ ОПТИЧЕСКОЙ СИСТЕМЫ И ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МОДЕЛИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17952 (дата обращения: 27.02.2026).



