Настоящая работа посвящена методам анализа экономических временных рядов (ВР) с долговременной памятью [1] на базе построения фазовых портретов [1]. Практика показала, что в современных условиях, к примеру, для российской экономики с её нестабильностью и финансовыми кризисами, классические экономическая теория и статистика, построенные на линейных равновесных моделях [1], оказались малопродуктивными или, более того, неадекватными. Это и неудивительно, поскольку переход от социалистического планового хозяйства к свободной рыночной экономике является крупным, можно сказать «бифуркационным» [2] поворотом, влекущим за собой необозримую совокупность «нелинейностей». Именно понятие бифуркации является ключевым понятием нелинейной науки («nonlinear science», как ее называют в англоязычной литературе). По существу, это математический образ «перехода количественных изменений в качественные».
Краткий анализ наиболее известных и апробированных подходов и методов предпрогнозного анализа и прогнозирования ВР можно найти в [3]. Важно отметить, что эти методы базируются либо на корреляционно-регрессионных моделях, либо на трендах, для представления которых выбирается наиболее подходящие экстраполяционные зависимости. Глубокий анализ временных рядов экономических, финансовых, инвестиционных процессов выявляет случай слабой адекватности этих моделей исследуемым временным рядам. Причиной тому является скрытая квазипериодичность, наличие долговременной памяти и дробной фрактальной размерности, присущей временным рядам инвестиционных показателей, используемых в зоне финансовых рисков. В силу этого обстоятельства в работе [4] для построения прогнозирования ВР с памятью предложен новый подход, который базируется на использовании клеточных автоматов [5] и математического аппарата нечетких множеств [6].
Для многих реальных ВР условие независимости уровней рассматриваемого ВР не выполняется в силу того, что отражаемые этими ВР социально-экономические процессы и системы обладают долговременной памятью [1]. В простейшем определении принято говорить, что ВР обладает (долговременной) памятью, если значение (числовое, лингвистическое и т.д.) какого-либо наблюдаемого уровня данного ВР зависит от значений определенного количества уровней, непосредственно предшествующих наблюдаемому уровню. При этом количество этих «непосредственно предшествующих уровней» называют термином «глубина памяти» рассматриваемого ВР. Численную оценку глубины памяти можно получить с помощью алгоритма R/S-анализа [1], подробное описание вычислительной схемы которого можно найти в [7,8]. Для прогнозирования ВР с памятью достаточно высокую надежность обеспечивает прогнозная модель, построенная на базе клеточного автомата [4].
В настоящей работе для получения предпрогнозной информации авторами используется инструментарий фазового анализа временного ряда. Уровни рассматриваемого ВР представляют собой помесячные объемы инвестиций в основной капитал такого региона, как Карачаево-Черкесская республика (КЧР) за период 1999-2003 гг. для этого ВР используем обозначение ![]() ,
, ![]() ,
, ![]() , где индекс
, где индекс ![]() используем для сквозной нумерации месяцев рассматриваемого 5-летнего периода;
используем для сквозной нумерации месяцев рассматриваемого 5-летнего периода; ![]() - объем инвестиций в
- объем инвестиций в ![]() -ом месяце.
-ом месяце.
В целях наглядности и визуализации динамики ВР ![]() представляем его графически в виде столбчатой диаграммы, изображенной соответственно на рис.1.
представляем его графически в виде столбчатой диаграммы, изображенной соответственно на рис.1.
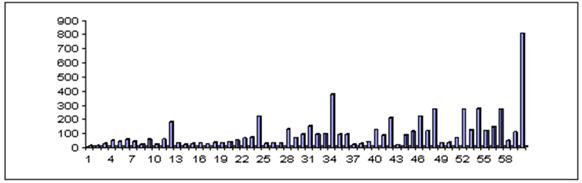
Рисунок 1. Графическое представление временного ряда объема инвестиций в основной капитал региона (на примере КЧР)
В процессе моделирования временных рядов методами нелинейной динамики (теории хаоса) [9,10] по-видимому, наиболее важным вопросом является вопрос о том, содержит ли траектория рассматриваемого ВР аттрактор (странный аттрактор) [9,10]. Для обоснования ответа на этот вопрос к настоящему времени разработан ряд алгоритмов и тестов (вычисление корреляционной размерности, максимального показателя Ляпунова, К-энтропии Колмогорова, BDS-тест, тест остатков Брока), общее описание которых можно найти в [9,10]. Вышеуказанные методы получили название метрических тестов. К последним, относится также инструментарий фрактального анализа [1,5].
Следует отметить достаточно высокую методическую и вычислительную сложность реализации метрических тестов. По этой причине они до настоящего времени не находили должного применения в реальном экономико - математическом моделировании. Судя по ряду публикаций, можно говорить о наметившейся тенденции использования так называемых графических тестов в процессе моделирования социально - экономических ВР методами нелинейной динамики. Можно упомянуть графический тест хаоса [9], предложенный Гилмором [11]. Этот тест выявляет неустойчивые квазипериодические периоды, заключенные в странном аттракторе. Для обнаружения таких орбит в рассматриваемом ВР наиболее удобным по своей реализации нам представляется подход, который можно называть термином «разложение фазового портрета на квазициклы».
Для анализируемого в этой работе ВР рассматривается последовательность его отрезков ![]() ,
, ![]() , называемых
, называемых ![]() - историями [9]. Здесь число
- историями [9]. Здесь число ![]() представляет собой размерность фазового портрета, который определяется в виде множества точек
представляет собой размерность фазового портрета, который определяется в виде множества точек
![]() ,
,
![]() (4)
(4)
в М-мерном евклидовом пространстве. При этом в целях визуализации это множество пред ставляется в виде траектории, которая получается путем соединения звеном (т.е. отрезком прямой или кривой) всякой пары соседних точек.
В целях визуализации на рис. 2 дано графическое представление фазового портрета представленного на рисунке 1 ВР объема инвестиций в основной капитал региона (на примере КЧР).
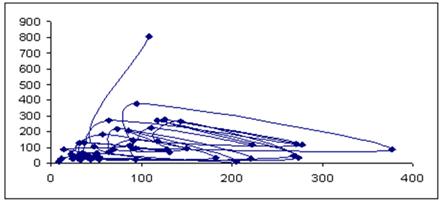
Рисунок 2. Фазовый портрет ВР объема инвестиций в основной капитал региона (на примере КЧР)
Упомянутое выше разложение фазового портрета на квазициклы в существенной мере базируется на визуализации графического представления (на экране дисплея) фрагментов данного фазового портрета. При этом принимается во внимание характер вращения звеньев, соединяющих соседние точки ![]() ,
, ![]() визуализируемого фрагмента рассматриваемого фазового портрета. Определение термина «квазицикл» в некотором смысле близко к определению общепринятого понятия «цикл». Различие между этими двумя понятиями состоит в том, что начальная и конечная точки квазицикла не обязательно должны совпадать. Конечная точка квазицикла определяется ее вхождением в окрестность начальной точки. При этом допускается самопересечение начального и конечного звеньев квазицикла, если это приводит к наилучшему сближению его начальной и конечной точек. На рис. 3 представлены все 9 квазициклов, которые получены после разложения на квазициклы фазового портрета изображенного на рис. 2. Эти квазициклы обозначаем через
визуализируемого фрагмента рассматриваемого фазового портрета. Определение термина «квазицикл» в некотором смысле близко к определению общепринятого понятия «цикл». Различие между этими двумя понятиями состоит в том, что начальная и конечная точки квазицикла не обязательно должны совпадать. Конечная точка квазицикла определяется ее вхождением в окрестность начальной точки. При этом допускается самопересечение начального и конечного звеньев квазицикла, если это приводит к наилучшему сближению его начальной и конечной точек. На рис. 3 представлены все 9 квазициклов, которые получены после разложения на квазициклы фазового портрета изображенного на рис. 2. Эти квазициклы обозначаем через ![]() , их длину – соответственно через
, их длину – соответственно через ![]() , последовательно номеруя индексом
, последовательно номеруя индексом ![]() ; Длины этих квазициклов получили значения
; Длины этих квазициклов получили значения ![]() =8,
=8, ![]() =5,
=5, ![]() =4,
=4, ![]() =8,
=8, ![]() =5,
=5, ![]() =5,
=5, ![]() =8,
=8, ![]() =8,
=8, ![]() =5. Для наглядности на рис. 4 представлена гистограмма частот в распределении этих длин.
=5. Для наглядности на рис. 4 представлена гистограмма частот в распределении этих длин.
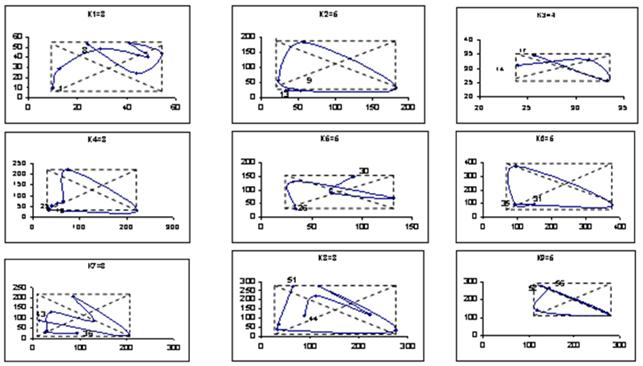
Рисунок 3. Разложение на квазициклы фазового портрета на рис. 2
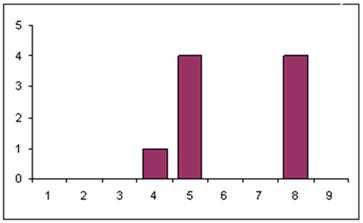
Рисунок 4. Гистограмма частот длин квазициклов ФП
Каждый из квазициклов изображен вместе с его габаритным прямоугольником. Точка пересечения диагоналей габаритного прямоугольника определяет собой центр вращения его квазицикла.
Рассматривая направление вращения звеньев квазициклов на рис. 3 (по часовой стрелке или против часовой стрелки), отметим, что явное большинство звеньев имеют направление вращения по часовой стрелке. Этот факт имеет принципиально важное значение с точки зрения предпрогнозного анализа. Вместе с тем, можно указать и такие квазициклы, в которых некоторые звенья имеют направление вращения против часовой стрелки, хотя доля звеньев с аномальным направлением вращения составляет 5/48, т.е. не более 10,5%.
Для всякого ВР представляемую его фазовым портретом (ФП) предпрогнозную информацию можно разделить на 3 группы. Первую группу составляет предпрогнозная информация, которая представляется разложением ФП этого ВР на квазициклы (см. рис.3).
Вторую группу составляет предпрогнозная информация, представляемая траекторией дрейфа центров квазициклов на рис. 5. Номера точек на этой траектории совпадают с номерами соответствующих квазициклов, а координаты этих точек представляют собой координаты центров соответствующих квазициклов.
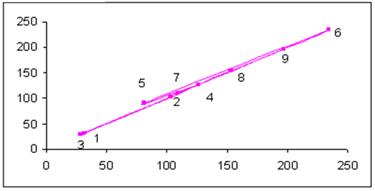
Рисунок 5. Траектория дрейфа центров квазициклов
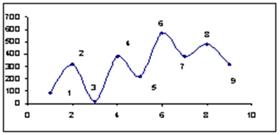
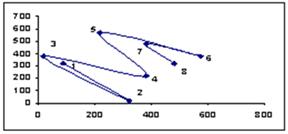
Третью группу составляет предпрогнозная информация, представляемая траекторией дрейфа полупериметров габаритных прямоугольников квазициклов, полученных в результате разложения рассматриваемого ФП, а также фазовым портретом этой траектории. На рис. 6 представлена соответственно траектория дрейфа полупериметров квазициклов фазовых портретов для рассматриваемого ВР объема инвестиций в основной капитал региона, а также фазовый портрет этой траектории.
а) б)
Рисунок 6. Траектория дрейфа полупериметров квазициклов (а) и ее фазовый портрет (б)
На основании предложенного инструментария фазового анализа для рассматриваемого ВР ![]() представляется возможным сформулировать следующую информацию для дальнейшего прогнозирования этого ВР.
представляется возможным сформулировать следующую информацию для дальнейшего прогнозирования этого ВР.
1. Согласно представленной на рис. 5 траектории дрейфа центров ей присуща следующая закономерность. Имеет место отчетливо выраженная закономерность, состоящая в чередовании возрастания и убывания (т.е. движения по биссектрисе вверх и вниз) координат точек центров.
2. Подавляющее большинство (около 90 %) звеньев предыдущих квазициклов имеют направление вращения по часовой стрелке.
3. В представленном на рис. 3 разложении фазового портрета (4) (см. рис.2) на квазициклы в нем отсутствуют незавершенные квазициклы, т.е. последний квазицикл в этом разложении является завершенным.
На основании сформулированных выше выводов 1-3 представляется возможным высказать следующие рекомендации относительно прогнозирования уровня ![]() в рассматриваемом ВР
в рассматриваемом ВР ![]() . Значение прогнозируемого
. Значение прогнозируемого ![]() определяет собой прогнозируемое звено
определяет собой прогнозируемое звено ![]() (
(![]() ), которое принадлежит новому квазициклу, имеющему следующие характеристики: центр этого квазицикла представляется такой точкой 10 на рис.5, которая смещена от точки 9 в окрестности точки 8; а габаритный прямоугольник нового квазицикла по сравнению по сравнению по своим предшественником увеличен согласно тенденции траектории на рис. 6(а); звено
), которое принадлежит новому квазициклу, имеющему следующие характеристики: центр этого квазицикла представляется такой точкой 10 на рис.5, которая смещена от точки 9 в окрестности точки 8; а габаритный прямоугольник нового квазицикла по сравнению по сравнению по своим предшественником увеличен согласно тенденции траектории на рис. 6(а); звено ![]() (
(![]() ), вращаясь по часовой стрелке, с учетом нового габаритного прямоугольника оставит без существенного изменения ординату прогнозируемой точки на фазовом портрете. Иными словами, по своей сути прогноз сводится к тому, что прогнозируемое значение
), вращаясь по часовой стрелке, с учетом нового габаритного прямоугольника оставит без существенного изменения ординату прогнозируемой точки на фазовом портрете. Иными словами, по своей сути прогноз сводится к тому, что прогнозируемое значение ![]() будет мало отличаться от значения предшествующего уровня
будет мало отличаться от значения предшествующего уровня ![]() .
.
СПИСОК ЛИТЕРАТУРЫ
1. Петерс Э. Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка. – М.: Мир, 2000. – 333с.
2. Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории. – М.: Мир, 1999. – 335 с.
3. Сигел Э.Ф. Практическая бизнес-статистика. – М.: Издательский дом «Вильямс», 2002. – 1056 с.
4. Перепелица В.А., Касаева М.Д., Тебуева Ф.Б., Темирова Л.Г. Использование инструментария клеточных автоматов для формирования прогнозных нечетких значений урожайности на базе временного ряда //Известия вузов. Северо-Кавказский регион.– Ростов-на-Дону.– 2003.–№4 – С.5-11.
5. Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях: – Тюмень: Изд-во ТюмГУ, 2000. – 151 с.
6. Holden K., Peel D.A., Thomson J.L. Economic forecasting: an introduction. – Press Syndicate of the University of Cambridge, 1990. – 213 p.
7. Перепелица В.А., Тебуева Ф.Б., Узденов Р.Х. Квазициклы временных рядов жилищного строительства. /Труды III Международной конференции «Новые технологии в управлении, бизнесе и праве», г.Невинномысск, 30 мая 2003 г., Невинномысск: ИУБиП, 2003. – С. 159-163.
8. Перепелица В.А., Беляков С.С., Овчаренко Н.Ф. Фрактальный анализ временных рядов объемов инвестиций в основной капитал региона //Региональное приложение к журналу «Современные наукоемкие технологии».– 2004.– №2.– С.19-23.
9. Сергеева Л.Н. Моделирование поведения экономических систем методами нелинейной динамики (теории хаоса). – Запорожье: ЗГУ, 2002. – 227 с.
10. Шустер Г. Детерминированный хаос: Введение. – М.: Мир, 1988. – 240 с.
11. Gilmore C.G. A new test for chaos //Journal of economic behavior and organization, №22, 1993. – P. 209-237.
Библиографическая ссылка
Овчаренко Н.Ф., Джашеева Ф.М. ФАЗОВЫЙ АНАЛИЗ ЭКОНОМИЧЕСКОГО ВРЕМЕННОГО РЯДА ИНВЕСТИЦИЙ В ОСНОВНОЙ КАПИТАЛ РЕГИОНА // Современные проблемы науки и образования. 2006. № 2. ;URL: https://science-education.ru/ru/article/view?id=179 (дата обращения: 05.03.2026).



