Эффективность информационного процесса (ИП) сложных систем определяют управляющим воздействием (УВ), которое формируется на шаге принятия решения. В связи с этим необходимо проанализировать функционирование разработки математической модели ИП на каждом ее шаге, т. е. разработать информационную модель ИП [2,3]. Обозначим информацию
(1)
которая циркулирует в информационной структуре (ИС) для выработки УВ, где:
- базовая информация (БИ) ИП;
IО - обеспечивающая информация (ОИ) ИП.
Базовую информацию представим в виде:
(2)
где:
- информация, контролирующая текущие данные;
- информация, содержащая данные нормативных документов;
- дополнительная информация.
Обеспечивающая информация представляется в виде:
(3)
где:
IOn- n-ый элемент ОИ;
- количество элементов ОИ.
Будем считать, что 
- процедура над БИ, которая работает для получения n-го элемента ОИ,
где:
d1– параметры, необходимые для формирования конкретных данных;
d2- отбор необходимой информации из исходной информации;
d3 - сортировка отобранной информации;
d4 – процедуры, необходимые для формирования данных;
d5 – использование математических моделей для отобранных данных;
d6 - деловая графика, представляемая в виде списков, таблиц, столбовых диаграмм, секторных диаграмм и т.д.
Будем считать, что 
- совокупность УВ, воздействующие на объекты управления, где 
.
Управляющие воздействия U формируются лицом, принимающим решение (ЛПР) на основе 
и профессиональных данных. IO формируется на основе выражения:
(4)
Функция hn определяет необходимую совокупность и последовательность процедур dj 
, которые воздействуют на 
, для получения 
.
Следовательно, получение IО с использованием 
осуществляется на основе множества
(5)
Каждая функция hn представляет собой отдельную процедуру, которая разбивается на подфункции hnk. Подфункция hnk осуществляет к-ое действие набора действий D[1,4].
Подфункцию hnk можно представить в виде:
множество входных параметров 
, где 
- количество входных параметров;
множество выходных параметров 
, где 
- количество выходных параметров;
- процедуры над входным параметром Хпk , которые формируют выходные параметры Ynk.
Оценка времени обработки БИ. Основной объем IБ базируется на элементах
, поэтому можно сказать, что с определенной погрешностью можно оценить время обработки этого элемента в виде выражения 
, где
VБ- объем информации ;
-время обработки эталонного объема информации.
Функцию 
представим в виде
, где 
- эталонный объем .
Оценка времени получения ОИ осуществляется на основе функции hn, через процедуры Dn.
Процедуры D не всегда воздействуют на IOn тогда:
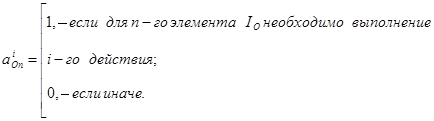
Оценка времени выработки п-го элемента IО может изменяться в зависимости от величины объема обрабатываемой БИ[1,4].
Обозначим 
- объем БИ, при воздействии процедуры i-го для формирования п-го элемента ОИ;
- время работы i-го действия для получения п-го элемента ОИ;
- время выполнения i-ой процедуры для формирования п-го элемента ОИ для эталонного объема БИ.
Для различных процедур время выполнения зависит от объема БИ и может:
почти не зависеть (например, d1);
зависеть линейно (например,d2);
зависеть не линейно (например, d4).
Следовательно, 
.
Процедуры qi могут быть различными, и поэтому время выработки п-го элемента ОИ определяется как:
(6)
Вычисление каждого нового элемента ОИ повышает объективность принимаемого решения. Однако ограниченность времени принятия УВ может не позволить сформировать все возможные элементы ОИ.
Обозначим
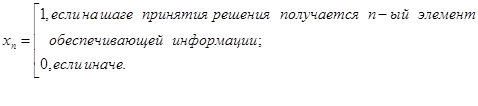(7)
Следовательно, формирование всей ОИ оценивается
как 
, где Х=(х1,х2,…,хN).
Оценка времени обработки ОИ вычисляется для каждого п-го элемента ОИ ЛПР, определяется величиной объема n-го элемента[5,7].
Обозначим:
- объем п-го элемента ОИ;
tLn - время обработки п-го элемента ОИ;
- время обработки п-го элемента ОИ для эталонного объема ОИ.
Для различных видов ОИ время ее обработки различное по следующим законам:
почти не зависит (обработка полностью соответствует решаемой задаче);
зависит линейно (обработка частично соответствует решаемой задаче);
зависит не линейно (произведена только выборка или сбор необходимой информации). Тогда 
. Время принятия решения определяется ЛПР на основе профессиональных знаний и обозначается как tR.
Время шага принятия решения оценивается как
(8)
Обоснованность принятия УВ выше в том случае, когда количество элементов ОИ больше. Однако не все элементы ОИ одинаково влияют на оптимальность принятия ЛПР[6].
Определим коэффициенты важности элементов ОИ Ω=(w1,w2,…,wN)
Следовательно, обоснованность вырабатываемого УВ ЛПР определяется как
(9)
Следовательно, математическую постановку задачи для оптимизации формирования УВ представим в виде[6,7].
Найти
X=Argmax O(X) (10)
при ограничениях
(11)
- допустимое время выработки УВ
(12)
Задача (2) - (4) относится к классу задач линейного целочисленного программирования. Все коэффициенты в целевой функции и ограничения положительны, что позволяет использовать для решения задачи метод Лаулера-Белла [8].
Рецензенты:
Филатов Г.Ф., д.ф.-м.н., профессор, профессор кафедры математики Военного учебно-научного центра Военно-воздушных сил, Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина, г. Воронеж;
Чопоров О.Н., д.т.н., профессор, проректор по научной работе Воронежского института высоких технологий, г. Воронеж.
Библиографическая ссылка
Сумин В.И., Колыхалин В.М., Смоленцева Т.Е. ОПИСАНИЕ ФУНКЦИОНИРОВАНИЯ ИНФОРМАЦИОННОГО ПРОЦЕССА СЛОЖНЫХ СИСТЕМ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17799 (дата обращения: 14.09.2024).