Исправление ошибок в каналах связи с шумами обычно осуществляется за счет применения помехоустойчивых кодов. В настоящее время теория помехоустойчивого кодирования предлагает большой выбор кодов и соответствующих им методов декодирования [2], характеризующихся различной эффективностью исправления ошибок. Одним из перспективных классов кодов являются самоортогональные коды (СОК), для декодирования которых обычно используют многопороговые декодеры (МПД), подробно описанные в [1]. Данные декодеры обеспечивают близкое к оптимальному декодирование правильно выбранных кодов со всего лишь линейной от длины кода сложностью реализации, зависящей от кодового расстояния применяемых кодов и числа итераций декодирования.
Помимо СОК, высокую эффективность исправления ошибок позволяют обеспечить коды с малой плотностью проверок на четность (Low-Density Parity-Check – LDPC) [6]. Эти коды представляют собой линейные коды, определяемые проверочной матрицей, содержащей в основном нули и сравнительно небольшое число единиц. Для LDPC кодов существуют очень эффективные алгоритмы декодирования, работающие с графом Таннера кода [4; 7] и позволяющие обеспечить исправление ошибок при уровне шума, всего на несколько десятых долей дБ меньшем теоретически возможного. Одним из наиболее простых из них с вычислительной точки зрения является min-sum алгоритм [8].
Из анализа проверочной матрицы СОК следует, что самоортогональные коды также имеют проверочную матрицу с малым числом единиц, и для них возможно применение итеративных методов декодирования низкоплотностных кодов, в частности min-sum декодера [3]. При этом по сравнению с существующими LDPC кодами при одинаковых параметрах СОК будут обладать существенно меньшей сложностью кодирования.
В [3] показано, что за счет использования min-sum алгоритма для декодирования СОК можно получить дополнительный энергетический выигрыш кодирования (ЭВК) по сравнению с МПД порядка 1 дБ при некотором увеличении вычислительной сложности, что не всегда является допустимым. В данной работе предлагается алгоритм декодирования СОК, позволяющий увеличить ЭВК по сравнению с МПД при меньшей сложности реализации по сравнению с min-sum алгоритмом.
Цель исследования
Разработка алгоритма, позволяющего увеличить энергетический выигрыш кодирования при декодировании самоортогональных кодов по сравнению с многопороговым декодером при меньшей сложности реализации по сравнению с min-sum алгоритмом.
Материал и методы исследования
Сначала оценим сложность реализации (в смысле количества выполняемых арифметических операций, эквивалентных сложению, требующихся для декодирования одного информационного бита) МПД и min-sum алгоритмов при декодировании СОК.
Для МПД сложность реализации пропорциональна кодовому расстоянию применяемых кодов d и числу итераций декодирования I. Количество арифметических операций, требуемых для декодирования одного информационного бита, примерно равно
. (1)
Сложность реализации min-sum декодера для СОК с кодовой скоростью 1/2 длиной n бит и k информационными битами с кодовым расстоянием d определяется следующим образом:
– на каждой итерации сначала вычисляют значения сообщений от каждого из n битовых узлов к связанным с ними проверочным. После использования оптимизации, представленной в [7], на этот этап требуется эквивалентное количество операций сложения
; (2)
– вычисляют значения сообщений от каждого из k проверочных узлов к связанным с ними битовым. На этот этап требуется
(3)
операций, эквивалентных сложению;
– после последней итерации формируется решение декодера. На это требуется эквивалентное число операций сложения
. (4)
В результате для декодирования всего кодового блока за I итераций выполняемое число операций, эквивалентных сложению, равно
. (5)
Тогда при декодировании одного информационного бита min-sum алгоритмом выполняется
(6)
операций, эквивалентных сложению.
Сравнение сложности реализации min-sum декодера и МПД при выполнении одинакового числа итераций декодирования СОК для типичных значений кодового расстояния показало, что min-sum декодер выполняет примерно в 6…7 раз большее число операций при декодировании, чем МПД. Это означает, что сложность декодирования при применении 6 итераций МПД алгоритма сопоставима со сложностью одной итерации min-sum алгоритма. Но при этом при равном числе итераций min-sum алгоритм обеспечивает несколько больший энергетический выигрыш (порядка 1 дБ), чем МПД. Для увеличения эффективности декодирования СОК при сохранении невысокой сложности можно применить комбинацию обсуждаемых алгоритмов декодирования. Причем на первых итерациях декодирования целесообразно использовать min-sum алгоритм, поскольку он позволяет работать при большем шуме в канале. После нескольких итераций min-sum алгоритма можно использовать МПД. При этом схема начинает эффективно декодировать применяемый код при большем уровне шума, чем при использовании МПД, но ее сложность по сравнению с МПД незначительно увеличивается, примерно в 2 раза. Структурная схема предлагаемого декодера представлена на рис. 1.
Рис. 1. Структурная схема предлагаемого составного декодера
Отметим, что на эффективность и сложность предложенной схемы влияние оказывают используемый СОК, число итераций min-sum алгоритма и число итераций МПД. Ниже выполнено исследование характеристик данной схемы при изменении данных параметров.
Результаты исследования и их обсуждение
Сначала рассмотрим характеристики различных алгоритмов декодирования блокового СОК с кодовой скоростью R = 2/4, кодовым расстоянием d = 9, длиной кода n = 20748 битов. Эти характеристики получены для канала с аддитивным белым гауссовским шумом при использовании двоичной фазовой модуляции. На рис. 2 кривые «30mtd» и «30minsum» отражают характеристики МПД и min-sum алгоритмов для этого СОК при использовании 30 итераций декодирования. Кривыми «3minsum+30mtd», «5minsum+30mtd», «7minsum+30mtd» и «9minsum+30mtd» представлены характеристики предложенной составной схемы декодирования при использовании в ней сначала соответственно 3, 5, 7 и 9 итераций min-sum алгоритма и потом 30 итераций МПД. Для сравнения на рисунке приведены характеристики схем декодирования только min-sum алгоритмом (кривые «8minsum», «10minsum», «12minsum», «14minsum»), сложность реализации которых соответствует сложности рассмотренных схем, использующих два алгоритма. Из графиков видно, что чем больше итераций с min-sum алгоритмом мы применяем в предложенной схеме, тем больше выигрыш по сравнению с МПД, но и тем больше сложность реализации. При использовании более 9 итераций min-sum алгоритма составная схема не дает выигрыша по сравнению только с min-sum алгоритмом при одинаковой сложности реализации.
Итак, для этого СОК при использовании предложенного составного декодера, включающего МПД и min-sum алгоритмы, мы получили выигрыш порядка 0,75 дБ по сравнению с МПД при использовании 9 итераций min-sum алгоритма. Эта схема оказывается чуть больше, чем в два раза, сложнее МПД по числу выполняемых операций. По сравнению с использованием только min-sum алгоритма получается ухудшение эффективности всего на 0,3…0,35 дБ при двукратном уменьшении сложности.
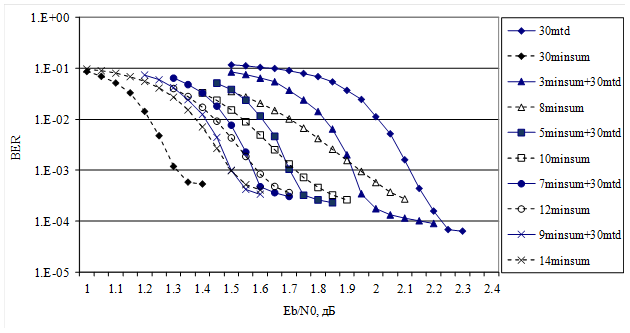
Рис. 2. Характеристики для СОК с n = 20748 и d = 9
Результаты исследования эффективности min-sum алгоритма декодирования СОК в [3] показывают, что min-sum декодер для различных СОК ведет себя так же, как и МПД. В итоге при использовании min-sum декодера можно применять подходы увеличения эффективности, разработанные для МПД, такие как применение параллельного кодирования, кодов с выделенными ветвями, кодов устойчивых к размножению ошибок, каскадирования с простейшими внешними кодами и др. [1]. Другими словами, хорошие СОК для МПД также являются хорошими СОК для min-sum декодера. В данной работе для увеличения эффективности предложенной схемы декодирования используем блоковый СОК с выделенными ветвями с длиной n = 31824, скоростью R = 8/16 (у кода 8 информационных и 8 проверочных ветвей) и кодовым расстоянием d = 17, структура которого представлена в таблице на рис. 3.
|
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
7 |
|
2 |
2 |
1 |
0 |
1 |
1 |
0 |
0 |
7 |
|
|
1 |
2 |
2 |
0 |
1 |
1 |
1 |
0 |
8 |
|
|
1 |
2 |
2 |
0 |
1 |
1 |
1 |
1 |
9 |
|
|
2 |
1 |
2 |
1 |
0 |
1 |
1 |
1 |
9 |
|
|
2 |
1 |
2 |
1 |
0 |
0 |
1 |
1 |
8 |
|
|
2 |
2 |
2 |
1 |
0 |
0 |
0 |
1 |
8 |
|
|
|
|
||||||||
|
4 |
4 |
4 |
12 |
12 |
12 |
12 |
12 |
72 |
|
Рис. 3. Структура СОК с выделенными ветвями
В ячейках таблицы размера 
указано число символов j-й информационной ветви СОК, участвующих в формировании i-й проверочной ветви кода. Сумма всех чисел в i-й строке определяет размерность проверок СОК, построенных на i-й проверочной ветви с учетом информационных символов всех восьми информационных ветвей. Эти суммы проставлены в правом столбце таблицы. Сумма чисел в j-м столбце является общим числом проверок относительно символов j-й информационной ветви и определяет кодовое расстояние для этой ветви. Для рассмотренного кода проверки восьмой ветви, имеющие очень большую размерность, при большом шуме с вероятностью, близкой к 0,5, являются неправильными. Поэтому на первых итерациях декодирования проверки этой ветви и при применении МПД, и при применении min-sum алгоритма не используются. Кроме повышения эффективности, это в несколько раз дополнительно снижает сложность схемы декодирования.
Далее рассмотрим характеристики предложенной составной схемы декодирования рассмотренного СОК с общим числом итераций, равным 35. На рис. 4 кривыми «35mtd» и «35minsum» представлены характеристики декодеров при использовании только МПД или min-sum алгоритмов декодирования с 35 итерациями. Названия остальных кривых на рис. 4 включают названия применяемых алгоритмов декодирования и число итераций. Из полученных графиков видно, что при одинаковом числе итераций (35 итераций) эффективность МПД примерно на 1,4 дБ хуже эффективности min-sum алгоритма, но при этом сложность его реализации в семь раз меньше. При использовании min-sum алгоритма вместе с МПД мы получаем выигрыш от 0,2 до 1,1 дБ по сравнению с МПД при увеличении сложности декодера в 2…3 раза. При увеличении количества используемых итераций min-sum алгоритма эффективность предложенной схемы декодирования увеличивается.
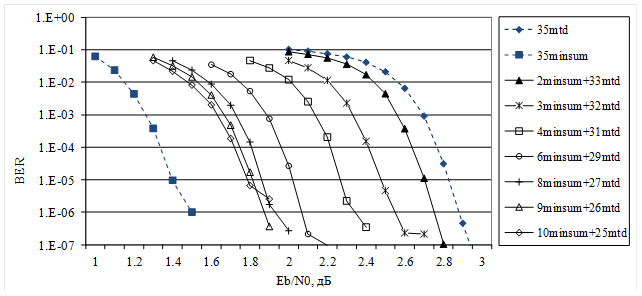
Рис. 4. Характеристики для СОК с n = 31824 и d = 17
Итак, для этого СОК при использовании сочетания МПД и min-sum алгоритмов мы получили выигрыш до 1,1 дБ по сравнению с МПД при использовании 9 итераций min-sum алгоритма и 26 итераций МПД. По сравнению с использованием только min-sum алгоритма получается ухудшение эффективности всего на 0,3…0,4 дБ при примерно трехкратном уменьшении сложности.
Заключение
Представленные результаты исследования показали, что при добавлении в схему многопорогового декодирования нескольких итераций декодирования по алгоритму min-sum область эффективной работы декодера приближается к пропускной способности канала на несколько десятых долей дБ при незначительном увеличении сложности реализации. Эффективность предложенного составного декодера зависит от используемого СОК, количества итераций min-sum и МПД алгоритмов, используемых в нем.
Работа выполнена при поддержке гранта Президента РФ (грант МД-639.2014.9) и РФФИ (грант 14-07-00824).
Рецензенты:
Костров Б.В., д.т.н., профессор, заведующий кафедрой «Электронные вычислительные машины» ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань;
Шибанов А.П., д.т.н., профессор, профессор кафедры систем автоматизированного проектирования вычислительных средств ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.
Библиографическая ссылка
Гринченко Н.Н., Као В.Т., Овечкин Г.В. ДЕКОДИРОВАНИЕ САМООРТОГОНАЛЬНЫХ ПОМЕХОУСТОЙЧИВЫХ КОДОВ С ПОМОЩЬЮ МНОГОПОРОГОВОГО И MIN-SUM АЛГОРИТМОВ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17793 (дата обращения: 07.10.2024).