В современных условиях конкурентной борьбы производитель должен обеспечивать высокое качество продукции при доступной цене. Достижение этих целей невозможно без создания оптимальных производственных условий, направленных на совершенствование технологических процессов и системы контроля на предприятии [3]. Система контроля на предприятиях строительной индустрии, как правило, включает в себя три составляющие: входной контроль, операционный контроль и приемочный контроль. Совершенствование данных методов контроля позволяет значительно сократить издержки производства при постоянном повышении качества продукции [2,4]. Особый интерес в данных условиях вызывает анализ точности и стабильности технологических процессов, который сегодня не мыслим без использования статистических методов.
Статистические методы хорошо зарекомендовали себя как инструменты качества и применяются в случаях, когда по результатам ограниченного числа наблюдений требуется установить причины улучшения или ухудшения точности и стабильности технологических процессов или работы технологического оборудования. Под точностью технологического процесса понимают свойство технологического процесса, обусловливающее близость действительных и номинальных значений параметров производимой продукции. Под стабильностью технологического процесса понимают свойство технологического процесса, обусловливающее постоянство распределений вероятностей для его параметров в течение некоторого интервала времени без вмешательства извне [5]. В свою очередь обеспечение стабильности и точности производственного процесса оказывает влияние на качество готовой продукции [4].
Системы управления предприятием или процессами в области качества требуют применения статистических методов:
-
методов анализа оценки качества продукции;
-
методов регулирования технологических процессов;
-
методов приемочного контроля качества и т.д.
Применение данных методов позволяет:
-
выявлять случайные и систематические показатели, способные привести к появлению дефектов;
-
проверять соблюдения требований ГОСТов, СНИПов и нормативных документов;
-
выявлять потенциальные резервы производства;
-
определить технические нормы и допуски выпускаемой продукции;
-
правильно осуществить выбор технологического оборудования и план проведения испытаний.
Существует несколько «классических» задач.
1. Выявить соответствие показателей качества выпускаемой продукции и эталонного изделия. Данная задача сводится к анализу математических ожиданий, и заключается в проверке нулевой гипотезы: 
, где
Х – случайная величина, значения которой определяют результат испытаний (наблюдения);
a – значение эталонного изделия.
2. Выявить отличие рассеивания показателя качества выпускаемой продукции от эталонного изделия. Данная задача сводится к сравнению дисперсий и заключается в проверке нулевой гипотезы: 
.
В данной работе для анализа стабильности технологического процесса предлагается проверить однородность двух независимых выборок, а именно осуществить сравнение их функций распределения и проверку нулевой гипотезы: 
.
Постановка задачи
В заводских лабораториях, отделах качества предприятий, как правило, для оценки стабильности технологического процесса прибегают к построению гистограмм для исследуемой случайной величины, составлению контрольных карт за отчетный период (например, неделя или месяц) и последующему их анализу.
Предлагаемая методика может быть сведена к проверке однородности двух независимых выборок (извлеченных из одной и той же генеральной совокупности), а именно к сравнению их функций распределения.
Одну выборку в данном случае можно считать базовой, когда качество выпускаемой продукции соответствовало всем техническим и нормативным требованиям (причем числовые характеристики данной выборки могут быть определены), а вторая выборка является исследуемой и призвана выявить улучшение (ухудшение, стабильность) технологического процесса по некоторому показателю.
Рассмотрим пример реализации предлагаемой методики по оценке стабильности технологического процесса производства бетона М150. Анализ проводился на основе данных прочности при сжатии (
) контрольных образцов в возрасте твердения 28 суток (таблица).
Независимые выборки из общей генеральной совокупности
|
Порядковый номер |
Базовая выборка |
Исследуемая выборка |
|
1 |
151 |
160 |
|
2 |
161 |
152 |
|
3 |
160 |
152 |
|
4 |
158 |
161 |
|
5 |
154 |
158 |
|
6 |
151 |
159 |
|
7 |
160 |
158 |
|
8 |
151 |
160 |
|
9 |
158 |
153 |
|
10 |
152 |
160 |
|
11 |
161 |
151 |
|
12 |
152 |
157 |
|
13 |
158 |
158 |
|
14 |
160 |
154 |
|
15 |
160 |
151 |
|
16 |
154 |
159 |
|
17 |
154 |
151 |
|
18 |
159 |
152 |
|
19 |
161 |
158 |
|
20 |
|
151 |
|
Объем выборки |
|
|
)
)
В среде Statistica 10 для наглядности результатов испытаний были построены гистограммы распределений базовой и исследуемой выборок с наложенными на них плотностями нормального распределения и получены значения статистик (чем меньше величины статистики Колмогорова–Смирнова, тем ближе распределение случайной величины к нормальному).
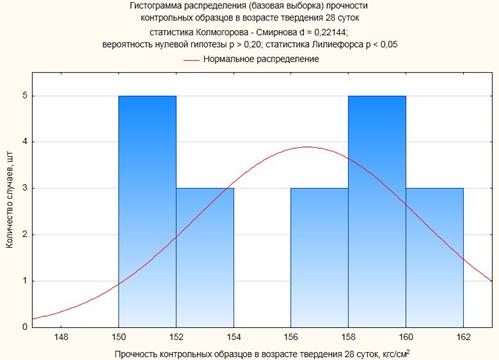
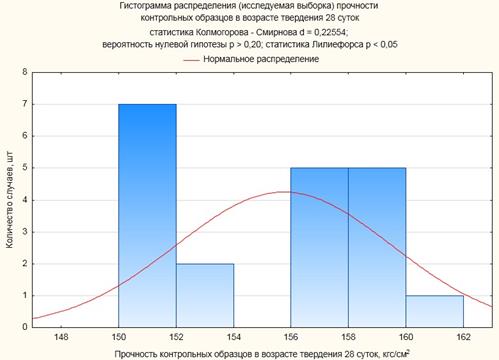
Гистограммы распределений базовой и исследуемой выборок
В качестве критерия для проверки однородности двух независимых выборок 
и 
воспользуемся критерием Вилкоксона, несомненным достоинством которого является возможность применения к случайным величинам с неизвестным законом распределения (обязательно лишь требование непрерывности случайных величин).
Данный критерий при заданном уровне значимости 
состоит в проверке нулевой гипотезы 
об однородности двух независимых выборок объемов 
и 
(
) при конкурирующей гипотезе 
. Ход проверка нулевой гипотезы несколько изменяется в зависимости от объема выборки и условно делится на два случая [1, с. 343–346]:
1) объем обеих выборок не превосходит 25;
2) объем хотя бы одной из выборок превосходит 25.
В рассматриваемом примере объем обеих выборок не превосходит 25.
Проверка критерия Вилкоксона
На первом этапе проверки критерия необходимо расположить варианты обеих выборок (таблица) в возрастающем порядке, т.е. в виде одного вариационного ряда:
151, 151, 151, 151, 151, 151, 151, 152, 152, 152, 152, 152, 153,
154, 154, 154, 154, 157, 158, 158, 158, 158, 158, 158, 158, 159, 159,
159, 160, 160, 160, 160, 160, 160, 160, 161, 161, 161, 161
(здесь жирным выделены варианты первой выборки),
и найти в этом ряду наблюдаемое значение критерия 
– сумму порядковых номеров вариант первой выборки:
,
Вторым этапом является определение верхней и нижней критических точек при заданном уровне значимости 
(например, 
):
1) нижняя критическая точка 
находится по таблицам критических точек критерия Вилкоксона [1, с. 471]:
,
;
2) верхняя критическая точка 
определяется по формуле:
.
Если 
или 
– нулевую гипотезу отвергают. Если 
– нет оснований отвергнуть нулевую гипотезу.
Из проведенных выше вычислений видно, что
,
и нет оснований отвергнуть нулевую гипотезу.
Следовательно, эталонная и исследуемая выборки имеют одинаковые функции распределения, и технологический процесс производства бетона М150 стабилен.
Выводы
Предлагаемая методика не требует построения гистограмм и контрольных карт и дает возможность быстро провести анализ точности и стабильности технологических процессов при обеспечении высокой достоверности результатов. Однако следует учитывать тот факт, что если по результатам анализа процесс окажется нестабильным, то требуется исследуемую выборку изучать более детально с целью выявления причин нестабильности процесса и ухудшения качества продукции.
Рецензенты:
Логанина В.И., д.т.н., профессор, зав. кафедрой «Управление качеством и ТСП», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;
Данилов А.М., д.т.н., профессор кафедры математики и математического моделирования, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Библиографическая ссылка
Тарасов Д.В., Тарасов Р.В., Макарова Л.В., Слепова И.Э. МЕТОДИКА ОЦЕНКИ СТАБИЛЬНОСТИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА ПРИ ПРОИЗВОДСТВЕ ПРОДУКЦИИ СТРОИТЕЛЬНОГО НАЗНАЧЕНИЯ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17674 (дата обращения: 19.04.2024).