При разработке тренажных и обучающих комплексов одной из актуальных задач является количественная оценка оператором устойчивости и управляемости объектом по данным функционирования целостной человеко-машинной (эргатической) системы. Напомним, устойчивость рассматривается, как способность объекта без вмешательства оператора сохранять заданный режим функционирования; а управляемость - должным образом реагировать на отклонение органов управления (для авиационной эргатической системы - рулей высоты, поворота и элеронов). Очевидна связь между равновесием, устойчивостью и управляемостью. Так, в общем случае движение самолета является весьма сложным, поэтому для простоты и удобства анализа на начальном этапе осуществляют декомпозицию (разложение) [2,4] на простейшие виды: продольное и боковое. Ограничимся количественной оценкой указанных характеристик объекта, исходя из параметров продольного движения.
Воспользуемся известными уравнениями [1] движения объекта с системой управления для короткопериодической составляющей:
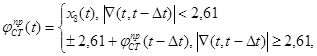
где
Во всех уравнениях, кроме последнего, искомые функции рассматриваются в точке t:
Для симметрии введем:
(
- равенство по определению).
Система приведется к виду:
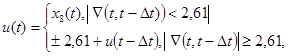
где:
Принято:
В линейной зоне (
) будем иметь:
Подставив
; 
окончательно получим систему уравнений короткопериодического движения в виде:
(1)
Для некоторых используемых структурных схем САУ 
можно заменить на 
что существенно облегчает исследование вопросов динамики. В этом случае уравнения динамики имеют вид:
В простейшем случае короткопериодическая составляющая продольного движения описывается системой:
(2)
Для оценки динамических характеристик объекта в [3, 6] предлагается функционал:
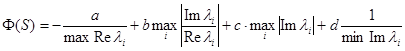,(3)
- корни характеристического полинома. Для системы второго порядка функционал представится в виде
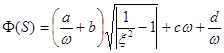,(4)
, 
- след матрицы 
- detA.
Выбор весовых коэффициентов нетривиален (связан с определением по данным нормального функционирования корреляционной зависимости между 
и 
, 
).
Воспользуемся предложенным функционалом для оценки динамических характеристик объекта с САУ (частный случай (1)):
(5)
- координаты САУ; 
- входные воздействия; 
- коэффициенты усиления.
Упростим (5), введя новые переменные
и рассматривая 
как входной сигнал системы. Получим:
(6)
, 
,
.
Из 1 и 4-го уравнения следует
,
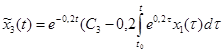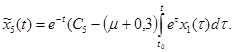
Из малости времени регулирования t - t0 значений 
следует слабая зависимость 
и 
от 
(зависимость от 
отсутствует!). Поэтому и можно рассматривать как входные воздействия системы с матрицей
.
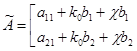
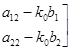Зависимость от параметров САУ определится по формулам перехода от 
к 
, в частности,
С учетом
влияние САУ на динамические характеристики системы можно оценить по смещению точки (
,
) относительно ( , ) на плоскости 
.
Множество объектов отнесем к 
-му классу в выбранной N-балльной шкале, если удовлетворяется условие
.
Границы областей 
для объектов -го класса определятся значениями 
, которые представляются в виде двух однозначных ветвей кривой
(
;
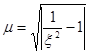) функции 
а именно:
.
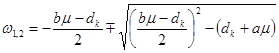В частности, класс =3,5 определяется по указанным формулам при 
, классу =6,5 соответствует значение 
(рисунок).
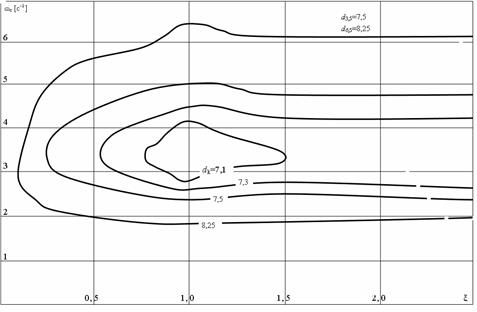
К классификации объектов на плоскости .
Таким образом, свойства системы (6) полностью определяются матрицей ; а оценку объекта для системы (5) можно производить по оценкам для системы (2). Приведенный подход неоднократно использовался при настройке параметров реальных систем [5,7,8].
Рецензенты:
Родионов Ю.В., д.т.н., профессор, заведующий кафедрой «Эксплуатация автомобильного транспорта» декан автомобильно-дорожного института ПГУАС, г. Пенза;
Кошев А.Н., д.х.н., профессор, профессор кафедры «Информационно-вычислительные системы» Пензенского государственного университета архитектуры и строительства, г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Сухов Я.И. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ХАРАКТЕРИСТИК ОБЪЕКТА ПО УПРАВЛЯЕМОСТИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17556 (дата обращения: 04.11.2025).