Искусственная нейронная сеть (ИНС) – математическая модель, моделирующая работу нейронов головного мозга человека. Одной из основных задач ИНС является анализ информации и определение свойств поступающих новых данных на основе проведённого анализа. В связи с высокой скоростью развития информационных технологий объём и разнородность анализируемых данных постоянно возрастает, в результате чего ИНС работает с большей погрешностью [4,5]. Основной задачей, решаемой в ходе данного исследования, является повышение однородности данных, обрабатываемых искусственной нейронной сетью. Одним из способов решения данной проблемы является кластеризация.
Кластерный анализ – методика разделения множества данных на подмножества таким образом, чтобы каждый кластер состоял из «схожих» объектов, а объекты разных кластеров имели сильные отличия [1]. Методы кластеризации имеют наибольшую актуальность в следующих случаях:
- обрабатываемые данные имеют большой объём;
- отсутствует заранее классифицированная обучающая выборка;
- нет предварительной информации об описании, границах и количестве классов обрабатываемых данных [2].
Целью данного исследования является снижение числа ошибок при работе нейронной сети.
Задачи:
1. Выбор архитектуры нейронной сети.
2. Повышение однородности анализируемых искусственной нейронной сетью данных.
3. Выбор метода кластеризации.
4. Разбиение нейронной сети на подсети.
Материалы и методы исследования
Кластер, один из основных терминов кластерного анализа, – группа из элементов со схожими свойствами. Слово «кластер» образовано от английского “cluster”, что означает пучок, группа, скопление, гроздь, куст. Не менее важное понятие центроид – центр кластера. Впервые задача кластеризации была поставлена в 1930-х годах [3].
Задача кластеризации заключается в разбиении множества обучающих примеров K на заранее заданное непересекающееся число подмножеств Ki таким образом, что
K = {K1, K2, K3, …,Kn}
![]() ,
,
где {K1, K2, K3, …, Kn} – кластеры множества K.
Элементы кластера Ki имеют схожие между собой свойства и несхожие свойства по отношению к элементам кластера Kj. Однако в ряде случаев используется менее жесткая методика кластеризации с использованием нечетких множеств. В данном случае кластеры характеризуются функциями членства, которые определяют степень принадлежности каждого элемента соответствующему кластеру [2].
Для разбиения большого объёма данных на кластеры используются неиерархические методы кластеризации. Одними из наиболее популярных являются алгоритмы k-meansи k-means++.
Метод k-средних (k-means) заключается в минимизации суммарного квадратического отклонения точек кластеров от их центров. Данный метод состоит из следующих этапов:
1. Число кластеров, на которые будет разбито множество элементов K, заранее известно.
2. Случайным образом определяются центры кластеров.
3. Вычисляется ![]() , где k – число кластеров, Si – полученные кластеры, i = 1,2,3,4,…,k, µi – центры кластеров.
, где k – число кластеров, Si – полученные кластеры, i = 1,2,3,4,…,k, µi – центры кластеров.
4. Вычисляется центр масс µ для каждого кластера
![]() , где Si – число элементов в кластере i.
, где Si – число элементов в кластере i.
5. Если центр масс изменился, то происходит переход к шагу 2, и продолжается работа алгоритма. Если не изменился, итерации завершаются.
Одной из модификаций алгоритма k-menas является алгоритм k-means++. Данный алгоритм был предложен в 2007 году Дэвидом Артуром и Сергеем Вассильвитским [6]. K-means++ является модификацией алгоритма k-means и направлен на поиск оптимальных начальных центров кластеров. Алгоритм состоит из следующих шагов:
1. Выбрать случайным образом центроид из всех имеющихся объектов множества K.
2. Для каждой точки определить значение квадрата расстояния до ближайшего центроида D(x)2.
3. Для каждой точки определить новый центр. Суммирование D(x)2 необходимо выполнять до тех пор, пока сумма не превысит Rand(0;1)•D(x)2. Как только это произойдет, суммирование можно остановить и определить текущую точку в качестве центроида. При выборе каждого следующего центроида нужно контролировать, чтобы он не совпал с одним из уже выбранных в качестве центроидов элементов.
Одним из критериев оценки эффективности кластеризации является сумма расстояний до центров кластеров. Для осуществления сравнения качества работы алгоритмов k-means и k-means++ был разработан программный комплекс; на его основе проведены исследования, результаты которых представлены в таблице 1, где V – сумма расстояний от точек до центров кластеров.
Из табл.1 видно, что алгоритм k-means++ лучше справляется с задачей кластеризации, чем k-means, поэтому для повышения точности работы нейронной сети предлагается использовать метод k-means++.
Таблица 1
Сравнение алгоритмов k-means и k-means++
|
Алгоритм кластеризации |
Число кластеров |
V |
Прирост точности (по сравнению с k-means), % |
|
k-means |
10 |
44713577494947,2 |
- |
|
k-means++ |
10 |
29870985390182,4 |
33.19 |
|
k-means |
8 |
44856741214940,31 |
- |
|
k-means++ |
8 |
30951151438308,81 |
31 |
|
k-means |
4 |
44999504532950,7 |
- |
|
k-means++ |
4 |
29422271430446,5 |
34 |
В качестве практической задачи для исследования эффективности работы кластеризованной нейронной сети была выбрана задача анализа сетевого трафика с целью определения наличия DDoS-атак. Для обучения была использована база [7], состоящая из 141946 обучающих примеров, 78,59 % из которых являются примерами DDoS-атак. В качестве базы для тестирования применялась база [7], состоящая из 283891 тестовых примеров, 78,66 % из которых являются атаками. Обучение происходит с использованием метода обратного распространения ошибки.
Так как нейронная сеть обрабатывает примеры разной структуры с различными свойствами, подобрать весовые коэффициенты каждого нейрона таким образом, чтобы анализ разнородных примеров происходил с большой точностью, достаточно сложно. Именно поэтому предлагается использовать кластеризованную нейронную сеть. Структура алгоритма обучения нейронной сети представлена на рис. 1.

Рис. 1. Структура алгоритма обучения кластеризованной нейронной сети
Алгоритм обучения кластеризованной нейронной сети выглядит следующим образом:
1. Происходит разбиение обучающей выборки K на кластеры K1, K2, …, Kn таким образом, что K = {K1, K2, K3, …, Kn}, ![]() . Нейронная сеть представляет собой множество подсетей N = {N1, N2, …, Nn}.
. Нейронная сеть представляет собой множество подсетей N = {N1, N2, …, Nn}.
2. Элемент Kij подается на нейронную сеть Ni, соответствующую кластеру Ki (элементы каждого кластера обрабатываются только на соответствующей им подсети).
Алгоритм анализа примеров при тестировании нейронной сети представлен на рис.2.
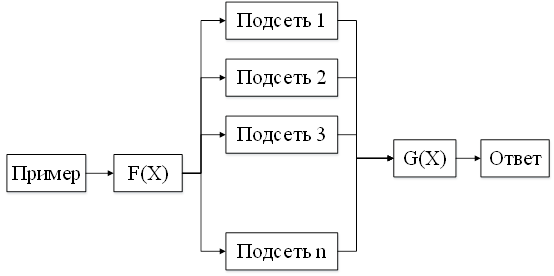
Рис. 2. Алгоритм анализа примеров при тестировании нейронной сети
Алгоритм состоит из следующих этапов:
1. Подаётся пример на нейронную сеть.
2. Функцией F(X) определяется, какому кластеру принадлежит данный пример и какая подсеть должна его обрабатывать.
3. Подсеть, обрабатывавшая пример, передаёт свой ответ функции G(X).
Выводы
Если множество тестовых примеров K` является конечным, можно определить, какая часть элементов принадлежит каждому кластеру.
Pi = Ki/K • 100 % – принадлежность элементов кластеру Ki
P`i = K`i/K` • 100 % – принадлежность элементов кластеру K`i
Если P`i>> Pi, необходимо произвести процесс обучения нейронной сети сначала. Подобное переобучение позволит избежать ошибок, связанных с недостаточным обучением подсетей. Например, если нейронную сеть обучать на 100 000 примеров, а на подсеть подать только 10 примеров для обучения (0.01 % от общего числа примеров), подсеть может недостаточно обучиться. Если же нейронную сеть тестировать на 200 000 примеров, а на подсеть подать 10000 (5 % от общего числа примеров), может возникнуть ситуация, когда данная подсеть будет часто ошибаться.
Среднее число ошибок в зависимости от числа кластеров представлено в табл. 2.
Таблица 2
Среднее число ошибок нейронной сети
|
Число кластеров |
Среднее число ошибок |
% ошибок нейронной сети |
|
Без разбиения |
1856 |
0,654 |
|
2 |
1314 |
0,463 |
|
3 |
1233 |
0,434 |
|
4 |
923 |
0,325 |
|
5 |
741 |
0,261 |
|
6 |
511 |
0,180 |
|
7 |
431 |
0,152 |
|
8 |
403 |
0,142 |
|
9 |
297 |
0,105 |
|
10 |
411 |
0,145 |
|
11 |
343 |
0,121 |
|
12 |
497 |
0,175 |
Как видно из табл. 2, для рассматриваемой задачи оптимальным является разбиение базы примеров на 9 кластеров, в результате чего число ошибок снижается более, чем в 6 раз.
К преимуществам кластеризованной нейронной сети с использованием алгоритма k-means++ можно отнести:
- повышение точности работы нейронной сети;
- работающие независимо друг от друга подсети позволяют реализовать механизм параллельных вычислений.
Рецензенты:
Ключко В.И., д.т.н., профессор, профессор кафедры ИСП Кубанского государственного технологического университета, г. Краснодар;
Пиотровский Д.Л., д.т.н., профессор, зав. кафедрой АПП Кубанского государственного технологическогоуниверситета, г. Краснодар.
Библиографическая ссылка
Частикова В.А., Остапов Д.С. ПРИМЕНЕНИЕ МЕТОДОВ КЛАСТЕРИЗАЦИИ ДЛЯ ПОВЫШЕНИЯ ТОЧНОСТИ РАБОТЫ НЕЙРОННЫХ СЕТЕЙ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17475 (дата обращения: 13.02.2026).



