В статье [4], посвященной применению симплекс-метода для решения задач динамического программирования, была приведена базовая линейная математическая модель (далее – базовая модель), используемая для формирования оптимального производственного плана с учетом возможности создания запасов ресурсов. Однако несложно заметить, что приведенная ранее модель содержит в себе лишь основные данные, учитываемые при планировании производственного плана и объема запасов ресурсов, в то время как количество факторов, очевидно воздействующих на деятельность организации и связанных с производством реальной продукции, значительно больше. Одним из важнейших факторов является фактор ликвидности, который определяет для организации уровень мобильности и возможности незамедлительной реализации по адекватной цене, как запасов ее ресурсов, так и продукции. Целью данной статьи является приведение способа учета данного фактора в линейной математической модели управления запасами предприятия в динамике.
Необходимость учета фактора ликвидности в математической модели обосновывается тем, что компания, производящая какой-либо продукт, может оказаться в положении, когда наблюдается избыток одних ресурсов и дефицит других. В частности, возможна ситуация, когда компания занимается изготовлением сложных и многокомпонентных продуктов, и в процессе производства базовые ресурсы уже превращены в некоторый продукт, не являющийся еще конечным, но при этом для завершения производственного цикла в силу тех или иных причин не хватает ряда ресурсов. В такой ситуации целесообразно рассмотреть возможность продажи избыточных запасов некоторых видов ресурсов или полуфабрикатов с целью приобретения дополнительных ресурсов, являющихся на данный момент дефицитными [1, 2].
В статье [4] был приведен ряд допущений и условий, в рамках которых результаты, рассчитанные на основании базовой модели с использованием симплекс-метода, будут адекватно отображать производственные планы и объемы запасенных ресурсов организации в различные моменты времени. Все эти допущения и условия будут актуальны и для расширенной модели динамического управления запасами организации с учетом фактора ликвидности.
Ликвидность фактического товара, будь то конечный продукт производства или ресурс, необходимый для его изготовления, характеризуется двумя параметрами: временем и стоимостью. Как известно, наибольшей ликвидностью обладает тот товар, который можно реализовать за его номинальную стоимость в минимальные сроки. Ликвидностью товара можно управлять путем изменения стоимости его продажи, то есть, снижая цену товара, мы имеем возможность сократить сроки, необходимые для его реализации. Математическая модель, которая представлена в данной статье, опирается на следующее предположение: цену ресурса всегда можно снизить до такого не отрицательного значения, что в любой рассматриваемый промежуток времени он будет гарантированно превращен в деньги путем его продажи.
При построении модели актуальным вопросом становится выбор формы учета конвертации одних ресурсов в другие. Это можно реализовать двумя способами: непосредственно введением в модель в качестве производственного ресурса денежных средств, либо рассматривать конвертацию ресурсов с применением коэффициентов, которые отображали бы соотношение цен данных ресурсов. В силу ряда специфических особенностей денежных средств, как ресурса, участвующего в производстве, предложено для конкретной модели в данной работе рассматривать второй вариант, без добавления в модель неравенства, учитывающего запасы денежных средств.
Таким образом, на основании выдвинутых предположений линейная модель динамического управления запасами с учетом фактора ликвидности ресурсов выглядит следующим образом [3, 6]:
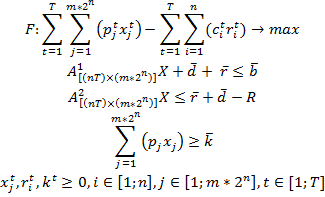
где:
– количество продукции 
-го вида, изготовленной по 
– производственной программе;
– чистая прибыль с единицы продукции -го вида, изготовленной по – производственной программе;
– затраты на хранение единицы ресурса i-го вида, приобретенного в момент времени t;
X – вектор, описывающий объем производственной продукции по всем типам программ для каждого конкретного временного интервала из рассматриваемого периода;
– производственные матрицы размерности 
которые описывают затраты ресурсов, привлекающихся на производство, соответственно, из двух различных источников, причем на изготовление каждого вида продукции различным способом. Они имеют блочную структуру, в которой блоки, содержащие ненулевые элементы, лежат на главной диагонали и описывают все производственные программы и затраты ресурсов на каждую из них в конкретном временном интервале;
– вектор размерности [n*T], описывающий предложение i-го ресурса на рынке в момент времени t;
– вектор размерности [n*T], задающий объем запаса i-го ресурса, создаваемого в момент t и доступного к использованию в производстве в момент времени t+1;
– вектор размерности [t], характеризующий минимальный размер чистой прибыли компании от производства, необходимого для поддержания работы в момент времени t.
– вектор, являющейся главной диагональю матрицы, которая определяется перемножением матриц 
;
L – матрица, описывающая коэффициенты попарной конвертации ресурсов, на практике может рассчитываться, как отношение фактической цены гарантированной продажи (в рассматриваемом периоде с учетом некоторого «штрафа» за скорость гарантированной продажи) имеющегося ресурса и рыночной цены ресурса, который планируется купить за счет вырученных средств, элемент матрицы 
– обозначает соответственно какой объем i-го ресурса мы можем приобрести за счет продажи единицы j-го ресурса;
R – матрица, описывающая фактическое количество купленных ресурсов в счет проданных запасов имеющихся ресурсов, на главной диагонали которой находятся 0. Весь объем купленных и проданных ресурсов будет отображаться в ней. Выглядеть в общем случае она будет следующим образом:
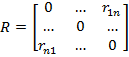
С учетом вышесказанного особое внимание стоит уделить строчкам матрицы, описывающим управление запасами компании. Рассмотрим отдельно произвольный случай работы с двумя равенствами для более наглядного описания. Пусть компания уже имеет некоторые запасы ресурсов i-го типа, но в рассматриваемый момент времени у нее возникла необходимость приобретения дефицитного ресурса j-го типа, без которого производство готовой продукции в принципе невозможно. Предложенная математическая модель может учесть возможность взаимной конвертации и предлагает оптимальное решение, фактическое описание которого отражается на значении целевой функции и, что более важно, в строках, описывающих саму конвертацию ресурсов, которые выглядят следующим образом:
Таким образом, можно наглядно увидеть, что в правой части равенств учитываются все возможные переходы. Однако необходимо внести некоторые уточняющие положения, при которых данная модель будет работать, и какие ситуации она не может описать:
-
В силу заданных ограничений ресурсы в конкретно взятый момент времени могут «двигаться» только в одном направлений и конвертировать один ресурс в другой нельзя сверх объема предлагаемого рынком второго ресурса в рассматриваемый период времени.
-
В отношении элементов матрицы L не выполняется следующее равенство
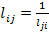, в силу того, что продажа каждого ресурса осуществляется со своим собственным «штрафом» за скорость гарантированной продажи, который будет варьироваться в зависимости от базовой ликвидности самого ресурса в данный момент времени в регионе, в котором работает компания, следовательно, цена продажи ресурса будет однозначно ниже рыночной при прочих равных условиях.
-
При работе данной модели допускается возможность опосредованной конвертации i-го ресурса в j-ый с использованием третьего ресурса, иначе говоря, модель учитывает спекулятивные возможности на рынке ресурсов в течение конкретного периода времени.
-
В силу отсутствия непосредственного учета запаса денежных средств, как ресурса необходимого для производства, все изменения цен на ресурсы или продукцию будут учитываться, как и в базовой модели исключительно через чистую прибыль от реализации единицы продукции (различных типов).
-
Данная модель может учитывать и использовать спекулятивные возможности на рынке ресурсов, возникающие в двух различных периодах времени, если таковые происходят.
Для наглядного изображения работы модели ниже приведен пример с конкретными числами, позволяющий увидеть ее потенциальные возможности. В практическом примере рассматривается случай, когда компания производитс последующей реализацией два типа конечного продукта и использует в производстве три типа ресурса в течение двух периодов.
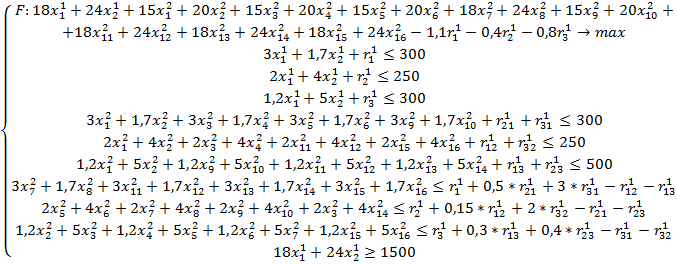
Стоит обратить внимание на условия рассмотренного примера. Во-первых, в примере ожидается рост цены 1-го типа ресурса во втором периоде по сравнению с первым периодом, данное увеличение было отражено в качестве уменьшения чистой прибыли от реализации продукции обоих видов, для производства которой используются ресурсы первого типа, приобретенные во втором периоде. А также увеличилось предложение ресурса третьего типа во втором периоде. Эти два изменения сыграют ключевую роль в выборе производственной программы и при управлении ресурсами организации.
Решение задачи можно представить в виде следующих векторов, характеризующих объемы производства, объемы запасов и количество конвертированных ресурсов, с учетом присвоенных им коэффициентов попарной ликвидности.
Объем производства продукции за первый и второй периоды в соответствии с выбранными производственными программами:
Объем сформированных запасов ресурсов каждого типа:
Объемы конвертации ресурсов:
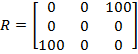
Интерпретируем полученные результаты:
-
Целевая функция достигла значения в 3 916,03 единиц (далее предположим, что это тыс. руб.);
-
В первом периоде было произведено 83,33 тыс. единиц продукции на сумму 1500 тыс. рублей и сформированы запасы ресурсов всех типов в следующих объемах:
(тыс. единиц);
-
Во втором периоде было произведено продукции первого типа – 101,9 тыс. ед., продукции второго типа – 34,88 тыс. ед. На общую сумму – 2 371,32 тыс. руб.
-
Продано 100 тыс. единиц ресурсов 3-го типа, с дальнейшим приобретением 300 тыс. единиц ресурсов 1-го типа.
Поскольку для решения задачи использовалась процедура симплекс-метода, наравне с векторами, отображающими объем производства, запасов и взаимной конвертации ресурсов, то были сформированы векторы двойственных оценок ресурсов и запасов ресурсов, в том числе конвертируемых (особенности их формирования и изменения рассмотрены в [4]):
Двойственные оценки ресурсов, предлагаемых на рынке в первом и втором периодах (приводятся в соответствии с порядком указания в задаче):
Двойственные оценки запасов ресурсов (приводятся в соответствии с порядком указания в задаче):
Особое внимание стоит обратить на тот факт, что с теми же данными базовая модель управления запасами компании в динамике [4] определяет следующее значение целевой функции – 3688,42 тыс. руб. Опираясь на данный факт, можно утверждать, что расширенная модель, учитывающая фактор ликвидности и возможность компании конвертировать свои ресурсы, в том числе и со спекулятивными целями, дает лучшее решение поставленной проблемы управления запасами.
Подводя итоги, следует сделать следующие выводы, а также предложения по развитию приведенной модели в будущем:
1) Приведенная модель доступна к применению на практике, позволяет более эффективно учитывать экономические условия, складывающиеся для конкретно взятой компании, и использовать большее число возможностей для получения дохода или минимизациииздержек, чем базовая модель.
2) Доступная для понимания интерпретация результатов делает данную модель перспективной для дальнейшего развития с целью учета большего числа факторов окружающей среды и возможностей компании.
3) Перспективным развитием модели представляется учет в ней запасов денежных средств, как ресурса, участвующего в производстве опосредовано через вложение в иные ресурсы, либо для конвертации. Кроме того, это позволит учитывать инфляционные, ценовые риски, а также ряд иных рисков в более наглядной форме.
4) Модель можно развивать как самостоятельный инструмент для формирования стратегии управления ресурсами, но также допустимо сделать ее частью более глобальной системы планирования с использованием более сложных технических средств. К примеру, используя ее в качестве элемента имитационного моделирования [5]. Однако это потребует значительного расширения количества учитываемых факторов, а также в целом потребуется более комплексный подход к их учету при формировании планов в сфере производства и управления ресурсами.
Рецензенты:
Петров Л.Ф., д.т.н., профессор кафедры математических методов в экономике ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва;
Халиков М.А., д.э.н., профессор кафедры математических методов в экономике ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.
Библиографическая ссылка
Титов В.А., Долгополов А.А. ФАКТОР ЛИКВИДНОСТИ В ЛИНЕЙНЫХ МОДЕЛЯХ ДИНАМИЧЕСКОГО УПРАВЛЕНИЯ РЕСУРСАМИ ПРОИЗВОДСТВЕННОЙ КОМПАНИИ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17427 (дата обращения: 05.10.2024).