Пусть принятым сигналом является реализация, содержащая 4 отражения от ионосферы зондирующих М-последовательностей и гауссов шум.
, (1)
где 
- принятая реализация сигнала, 
- комплексные амплитуды принятых М-последовательностей 
с временами прихода 
, 
- гауссов шум.
Тогда функционал правдоподобия, соответствующий данной системе, имеет вид:
, (2)
где 
, 
- корреляционная матрица и вектор корреляций соответственно.
Данный функционал зависит только от времён 
, определить которые можно, найдя его минимум.
Пусть мы хотим найти минимум функционала (2) в 4-мерном пространстве (
) при 
вычислениях в одном измерении, тогда количество расчетов, необходимых для нахождения решения, будет равно 
.
Пример.
Пусть имеется отраженный от ионосферы сигнал длительности 6.018 мс на несущей частоте 465 кГц. Интервал дискретизации сигнала составляет 0.2 мкс. Пусть ожидаемые времена прихода отраженных сигналов лежат в интервале от 1.0 до 5.3 мс. Если взять шаг сетки, по которой будет осуществляться поиск минимума функционала равным 5 мкс, то количество узлов на ребро составит 
, и число вычислений превысит 
.
Пусть машинное время вычисления одного значения функционала составляет примерно 6 мкс, тогда суммарное время для нахождения решения составит примерно 38 суток.
Важно отметить, что для обработки типовой ионограммы, построенной с шагом по частоте, равным 10 кГц, в интервале частот от 1 до 9 Мгц, необходимо обработать 800 файлов с записями отраженных сигналов, поэтому задачу минимизации нужно производить 800 раз. Отсюда следует огромное число лет, необходимое для решения задачи построения высотно-частотной характеристики – 83 года.
Как показывает пример, оптимизация необходима для решения поставленной задачи, основанной на применении теории оптимального приема.
Для наглядности перейдем от четырехмерной задачи к двумерной и рассмотрим реализацию, изображенную на рисунке 1 и имитирующую отражённый от ионосферы сигнал. Сигнал имеет следующие параметры: времена прихода первой и второй отраженной М-последовательностей соответственно равны 1.6 и 1.8 мс. Амплитуды сигналов одинаковы и равны 1.0 В, СКО гауссова шума равно 0.25 В.
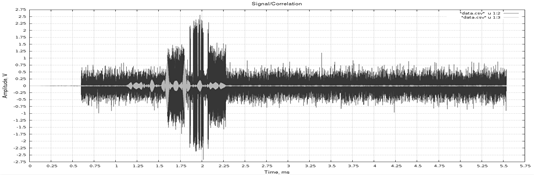
Рис. 1. Модельный сигнал (темно-серый) и его корреляционная функция (светло-серый).
Для данного сигнала построим функционал правдоподобия с шагом 5 мкс. Его внешний вид изображен на рисунке 2.
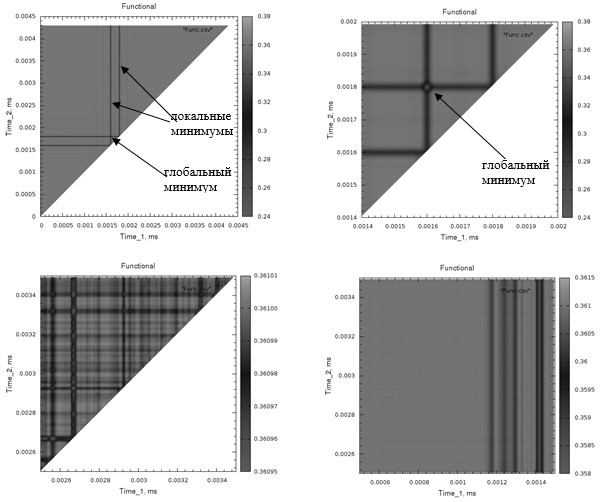
Рис. 2. Функционал правдоподобия.
Как видно из рисунка 2, функционал имеет ярко выраженный глобальный минимум в точке 
. Также существует ряд ярко выраженных локальных минимумов в точках, когда одно из значений 
равно истинному значению. Остальные локальные минимумы выражены менее сильно и связаны с видом сигнала, а именно с наличием боковых лепестков у корреляционной функции М-последовательности, а также с влиянием шума.
По внешнему виду функционала легко сделать вывод, что его минимизация нетривиальная задача. Т.к. глобальный минимум очень узок, то легко промахнуться, также велика вероятность остановки алгоритма в одном из локальных минимумов.
Существует огромное количество алгоритмов глобальной оптимизации, отличающихся принципом действия, скоростью сходимости, чувствительностью к локальным экстремумам и т.п. Огромное разнообразие этих алгоритмов определяется тем, что ни один из них не носит универсальный характер. Так, какие-то алгоритмы лучше приспособлены для решения одних задач, а другие для других.
Применение таких популярных алгоритмов, как DIRECT [1; 2], ISRES [4; 5], CRS [3; 6; 7], показало их недостаточную эффективность при решении указанной задачи, поэтому автором предложен алгоритм CRSM_LGM (контролируемый случайный поиск с локальными и глобальными мутациями).
Данный алгоритм является модификацией алгоритма CRS, предложенного W.L. Price [6; 7]. Базовый алгоритм CRS находит нового потенциального индивида в популяции на основании случайной комбинации нескольких индивидуумов, уже принадлежащих популяции. В случае если данный потенциальный индивид лучше самого худшего индивидуума в популяции, то он заменяет его.
Мы добавим в алгоритм процедуру глобальной и локальной мутации для уточнения решения как глобально, так и в окрестности некого локального минимума.
Работа всегда ведется с наихудшим индивидом в популяции или с новым индивидом, заменившим его в процессе работы базового CRS-шага.
Процедуры локальной и глобальной мутации принципиально не отличаются друг от друга, различия в них лишь в степени вносимого в координаты индивида «шума». Шум определен как аддитивный гауссовский со средним значением, равным нулю, и неким СКО, определенным пользователем. Стандартно СКО для локальной мутации – 25 минимальных шагов алгоритма, а для глобальной мутации четверть области определения одной из переменных.
После осуществления стандартного CRS-шага мы производим операцию глобальной мутации, причем делаем ее покоординатно, а именно «шатаем» значения одной из координат индивидуума и смотрим на значение его пригодности. Если она улучшилась, то заменяем старого индивида на нового. Так же поступаем для всех остальных координат.
Следующим шагом будет аналогичная процедуре глобальной мутации локальная мутация, призванная улучшить значения особи в окрестности некоего минимума.
Итак, шаг алгоритма CRSM_LGM представляет собой следующее.
-
Базовый CRS-шаг.
-
Глобальная покоординатная мутация индивида, полученного на предыдущем шаге (или наихудшего индивида в популяции в случае неудачного CRS-шага).
-
Локальная покоординатная мутация индивида, полученного на предыдущем шаге.
Эти шаги повторяются до тех пор, пока не наступит критерий остановки. На рисунке 2 приведены шаги алгоритма по достижению глобального минимума. Как видно из рисунка, алгоритм сходится к глобальному минимуму, эффективно преодолевая все локальные минимумы и исследуя окрестности глобального минимума.
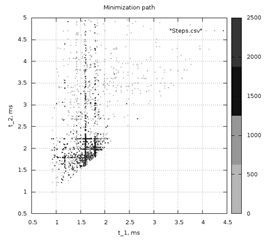
Рис. 3. Итерационный ход алгоритма CRSM_LGM.
Блок-схема алгоритма приведена на рисунке 4.
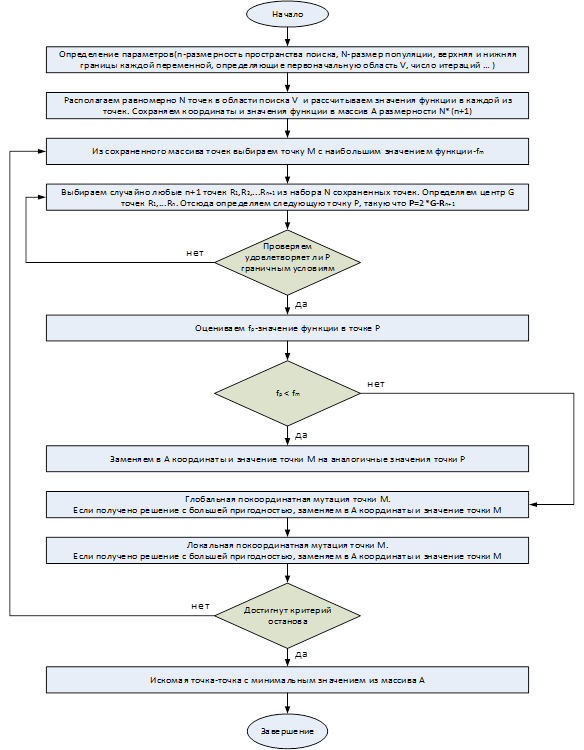
Рис. 4. Блок-схема алгоритма CRSM_LGM.
Приближенная зависимость числа вычислений целевой функции от размерности пространства поиска - 
, где - число вычислений, необходимых для расчета одномерной задачи, 
- размерность пространства поиска.
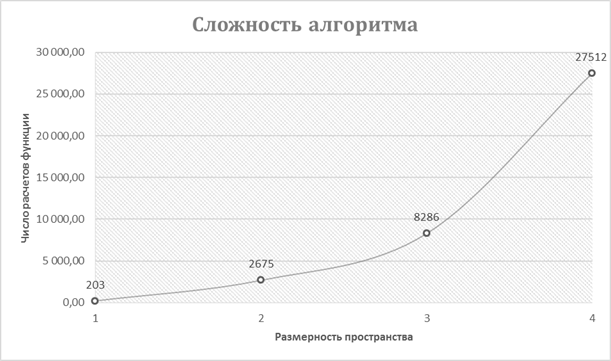
Рис. 5. Зависимость числа вычислений функции до сходимости алгоритма от размерности пространства поиска.
Пример. Вернемся к примеру, приведенному в начале главы, и оценим время обработки одной сигнальной записи в случае использования описанного алгоритма. Используя то же предположение, что машинное время вычисления одного значения функционала составляет примерно 6 мкс, получим оценочное время, требуемое для завершения расчета: 
. Это время, по сравнению с перебором по сетке, сократилось в 20 млн раз. Отсюда время расчета типовой ионограммы, без учета издержек на другие операции, составит 2 мин 12 секунд.
Приведенные в статье результаты показывают важность применения оптимизации в алгоритмах, построенных на использовании теории оптимального приема. Предложена новая модификация алгоритма CRS, адаптированная для минимизации функционалов, возникающих при решении задачи локации, основанной на применении теории оптимального приема.
Рецензенты:
Пахотин В.А., д.ф.-м.н., профессор, БФУ им. И. Канта, г. Калининград;
Никитин М.А., д.ф.-м.н., профессор, БФУ им. И. Канта, г. Калининград.
Библиографическая ссылка
Строков В.И. ПРИМЕНЕНИЕ ГЛОБАЛЬНОЙ ОПТИМИЗАЦИИ К РЕШЕНИЮ ЗАДАЧИ ЛОКАЦИИ, ОСНОВАННОЙ НА ПРИМЕНЕНИИ ТЕОРИИ ОПТИМАЛЬНОГО ПРИЕМА // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17421 (дата обращения: 20.04.2024).