Релятивистские представления о пространстве и времени возникли из достижений классической электродинамики, полученных к началу ХХ века. Скорость света в вакууме обрела статус параметра метрики единого пространства-времени. Впоследствии концепция вакуума как пустого пространства была отвергнута, а понятие фазовой скорости волны в среде приобрело большое значение (в частности, после открытия излучения Вавилова-Черенкова и создания концепции коллективного излучения). Эта скорость зависит не только от свойств среды, но и от параметров волны (дисперсия волн). Однако такое развитие электродинамики не оказало заметного влияния на развитие представлений о пространстве и времени.
Цель исследования
Целью исследования является выдвижение научной гипотезы о том, что вслед за вариацией фазовой скорости волны в среде следует говорить о вариации метрики пространства-времени в этой среде, одним из проявлений которой является возможность передачи информации в среде со скоростью, превышающей скорость света в вакууме.
Материал и методы исследования
Материалом исследования являются общепринятые основные аналитические модели волнового движения в диспергирующей линейной среде, в частности модели классической электродинамики изотропной бесстолкновительной плазмы. Обычно в них скорость движения материи отождествляется с групповой скоростью волны, что согласуется с релятивистскими представлениями о пространстве и времени. Но это противоречит идее Тейлора и Д. Бернулли о фундаментальной роли синусоидальных волн, раскрывающейся в понимании физического смысла волн общего вида через их частотное представление (уместно вспомнить научную дискуссию XVIII века «Спор о струне»). Следуя этой идее, мы отождествляем скорость движения материи с фазовой скоростью волны, так как она связывает частоту и волновое число, с которыми можно ассоциировать энергию и импульс волнового движения.
Результаты исследования и их обсуждение
Распространение плоской синусоидальной (монохроматической) бегущей волны описывается синусоидальной волновой функцией (осциллятором) прямоугольных декартовых пространственных координат ![]() ℝ,
ℝ, ![]() ℝ,
ℝ, ![]() ℝ и времени
ℝ и времени ![]() ℝ инерциальной системы отсчета (координатное и частотное представления здесь совпадают). Осциллятор может быть представлен в двух взаимно эквивалентных формах: вещественнозначной функции
ℝ инерциальной системы отсчета (координатное и частотное представления здесь совпадают). Осциллятор может быть представлен в двух взаимно эквивалентных формах: вещественнозначной функции ![]() (вещественный осциллятор) и комплекснозначной функции
(вещественный осциллятор) и комплекснозначной функции ![]() (комплексный осциллятор). Если ось
(комплексный осциллятор). Если ось ![]() коллинеарна волновому вектору, эти функции примут вид
коллинеарна волновому вектору, эти функции примут вид
![]() , (1)
, (1)
![]() ,
, ![]() , (2)
, (2)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ℝ – амплитуда (может быть скалярной, векторной или спинорной в зависимости от выбора математического представления функций физического поля), комплексная амплитуда, круговая частота (
ℝ – амплитуда (может быть скалярной, векторной или спинорной в зависимости от выбора математического представления функций физического поля), комплексная амплитуда, круговая частота (![]() для (1) и
для (1) и ![]() для (2)), проекция волнового вектора на ось
для (2)), проекция волнового вектора на ось ![]() и начальная фаза осциллятора,
и начальная фаза осциллятора, ![]() – его волновое число. Вектор скорости волны имеет проекцию
– его волновое число. Вектор скорости волны имеет проекцию ![]() на ось
на ось ![]() и модуль
и модуль ![]() .
.
Описание распространения в линейной среде плоской полихроматической волны проблематично в координатном представлении, но очевидно в частотном представлении, имеющем две взаимно эквивалентные формы: форму вещественнозначной волновой функции ![]() , определяемой надлежащей суперпозицией вещественных осцилляторов (1) с подходящими значениями параметров
, определяемой надлежащей суперпозицией вещественных осцилляторов (1) с подходящими значениями параметров ![]() ,
, ![]() ,
, ![]() ,
, ![]() , и форму комплекснозначной волновой функции
, и форму комплекснозначной волновой функции ![]() , определяемой надлежащей суперпозицией комплексных осцилляторов (2) с подходящими значениями параметров
, определяемой надлежащей суперпозицией комплексных осцилляторов (2) с подходящими значениями параметров ![]() ,
, ![]() ,
, ![]() , причем
, причем ![]() . Если для всех таких осцилляторов
. Если для всех таких осцилляторов ![]() (отсутствие частотной дисперсии), то эта константа имеет смысл проекции на ось
(отсутствие частотной дисперсии), то эта константа имеет смысл проекции на ось ![]() вектора скорости распространения волны, модуль же его равен
вектора скорости распространения волны, модуль же его равен ![]() .
.
При наличии же частотной дисперсии волны (случай диспергирующей волны) параметры каждого ее осциллятора связаны дисперсионным соотношением [13]
![]() , (3)
, (3)
характеризующим конкретную среду и имеющим вещественные корни вида
![]() ,
, ![]() , (4)
, (4)
причем одному соотношению (3) могут удовлетворять различные функции ![]() , отвечающие различным модам, а диспергирующая волна, как единое целое, образуется суперпозицией всех возможных для (3) мод. В этом случае распространение волны описывается двумя скоростями (фазовой и групповой), проекция на ось
, отвечающие различным модам, а диспергирующая волна, как единое целое, образуется суперпозицией всех возможных для (3) мод. В этом случае распространение волны описывается двумя скоростями (фазовой и групповой), проекция на ось ![]() и модуль вектора которых равны
и модуль вектора которых равны ![]() ,
, ![]() и
и ![]() ,
, ![]() . При этом величины
. При этом величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() для любой конкретной моды (4) являются значениями функций
для любой конкретной моды (4) являются значениями функций ![]() ,
, ![]() ,
, ![]() ,
, ![]() от
от ![]() , но численнозначное измерение каждой скорости для волны в целом не имеет физического смысла.
, но численнозначное измерение каждой скорости для волны в целом не имеет физического смысла.
Распространение в линейной среде плоской полихроматической диспергирующей волны может физически интерпретироваться как соответствующая эволюция динамической физической системы, представляющей собой данную среду. Как и эволюция любой другой динамической физической системы, эволюция среды в данном случае однозначно определяется уравнениями движения и начальными условиями, причём уравнения движения задают закон эволюции системы во времени и пространстве. Система уравнений движения представляет собой для конкретной моды (4) уравнения, задающие граничные условия, и интегродифференциальное уравнение волны для комплекснозначной волновой функции ![]() [13]
[13]
![]() , (5)
, (5)
ядро которого ![]() представляет собой обратное преобразование Фурье-функции
представляет собой обратное преобразование Фурье-функции ![]() , задающей дисперсионную кривую для данной моды:
, задающей дисперсионную кривую для данной моды:
![]() . (6)
. (6)
При этом в силу (6) для фиксированной моды (4) задание интегродифференциального уравнения (5) и задание уравнения дисперсионной кривой
![]() (7)
(7)
эквивалентны для определения класса волн, то есть любому частному решению уравнения (5) отвечает дисперсионная кривая (7) и, наоборот, любая комплекснозначная волновая функция, которой отвечает дисперсионная кривая (7), является частным решением (5). По крайней мере формально любая комплекснозначная волновая функция, удовлетворяющая дисперсионному соотношению (3), разлагается в сумму по всем модам (4) комплекснозначных волновых функций, каждая из которых является частным решением соответствующего моде уравнения (5) и отвечает для той же моды дисперсионной кривой (7), соответствующей ядру (6), то есть распространение плоской полихроматической волны в линейной диспергирующей среде имеет частотное представление в виде суммы интегралов Фурье
![]() (8)
(8)
по всем модам ![]() (4) для данного соотношения (3), где все комплексные амплитуды
(4) для данного соотношения (3), где все комплексные амплитуды ![]() подбираются так, чтобы удовлетворить заданным начальным и граничным условиям [13]. Особо выделим физически важный случай наличия двух мод
подбираются так, чтобы удовлетворить заданным начальным и граничным условиям [13]. Особо выделим физически важный случай наличия двух мод ![]() , различающихся знаком, тогда волновая функция (8) является суммой двух интегралов Фурье [13]:
, различающихся знаком, тогда волновая функция (8) является суммой двух интегралов Фурье [13]:
![]() . (9)
. (9)
Фазовая скорость диспергирующей волны в линейной среде может быть сколь угодно велика, но скорость информационного сигнала в ней обычно считается равной групповой скорости, которая всегда ограничена скоростью света в вакууме, если только для данной волны понятие групповой скорости имеет точный смысл (предполагается, что спектр такого сигнала целиком лежит в некоторой полосе частот ![]() ) [2]. Именно полосовой, а не точечный характер спектра реального сигнала, способного нести информацию, ограничивает скорость сигнала скоростью света в вакууме (монохроматический сигнал не несет информации).
) [2]. Именно полосовой, а не точечный характер спектра реального сигнала, способного нести информацию, ограничивает скорость сигнала скоростью света в вакууме (монохроматический сигнал не несет информации).
В результате такого рассмотрения вопроса передачи сигналов в диспергирующей линейной среде и успехов теории относительности в науке укоренились представления о невозможности передачи информации со сверхсветовой скоростью. Однако, на наш взгляд, принципиальные теоретические возможности сверхсветовой передачи информации открываются при использовании пространственно-частотного разделения информационного сигнала, распространяющегося в неоднородной диспергирующей линейной среде.
Неоднородность среды параметризуем одним числовым параметром, считая, что его значение возвращает известная функция круговой частоты плоской бегущей монохроматической волны и модуля фазовой скорости такой волны в среде с такой круговой частотой:
![]() . (10)
. (10)
Область среды (назовем ее рабочей областью), непосредственно используемая для передачи сигнала с пространственно-частотным разделением, изображена на рисунке 1 в прямоугольной декартовой системе пространственных координат в проекции на плоскость ![]() .
.
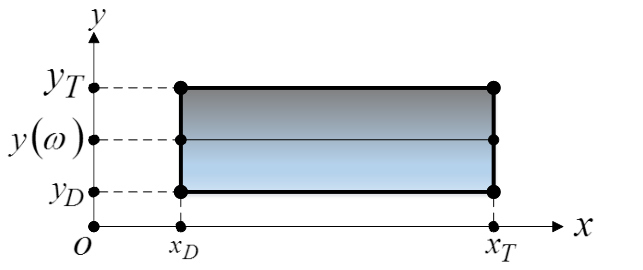
Рис. 1. Пространственно-частотное разделение информационного сигнала.
Рабочая область имеет форму прямоугольника с вершинами ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Сигнал передается от своей начальной пространственной локализации, которой является отрезок
. Сигнал передается от своей начальной пространственной локализации, которой является отрезок ![]() , до конечной
, до конечной ![]() . Суть пространственно-временного разделения состоит в том, что каждая монохроматическая составляющая сигнала, характеризующаяся своим значением круговой частоты
. Суть пространственно-временного разделения состоит в том, что каждая монохроматическая составляющая сигнала, характеризующаяся своим значением круговой частоты ![]() , пространственно разделяется с монохроматическими составляющими с другими ее значениями за счет того, что передается по своему индивидуальному маршруту – отрезку
, пространственно разделяется с монохроматическими составляющими с другими ее значениями за счет того, что передается по своему индивидуальному маршруту – отрезку ![]() , на всем протяжении которого параметр среды
, на всем протяжении которого параметр среды ![]() имеет постоянное значение, определяемое из (10), где
имеет постоянное значение, определяемое из (10), где ![]() – заданная строго возрастающая функция, например линейная
– заданная строго возрастающая функция, например линейная
![]() , (11)
, (11)
причем в любом случае выполнено: ![]() ,
, ![]() ,
, ![]() .
.
Такое согласование разделения маршрутов передачи монохроматических составляющих с характером неоднородности среды приводит к тому, что фазовые скорости всех монохроматических составляющих равны одному и тому же заранее заданному значению ![]() , не зависящему от частоты. Для такого информационного сигнала понятие групповой скорости волны теряет свой привычный смысл, фазовая скорость волны не зависит от частоты и обретает смысл скорости передачи сигнала подобно случаю отсутствия дисперсии. Если
, не зависящему от частоты. Для такого информационного сигнала понятие групповой скорости волны теряет свой привычный смысл, фазовая скорость волны не зависит от частоты и обретает смысл скорости передачи сигнала подобно случаю отсутствия дисперсии. Если ![]() выбирается большей скорости света в вакууме
выбирается большей скорости света в вакууме ![]() , то и скорость передачи информационного сигнала оказывается большей скорости света в вакууме. Рассмотрим в качестве примера однопараметрической линейной диспергирующей среды изотропную бесстолкновительную плазму.
, то и скорость передачи информационного сигнала оказывается большей скорости света в вакууме. Рассмотрим в качестве примера однопараметрической линейной диспергирующей среды изотропную бесстолкновительную плазму.
Дисперсионное соотношение (3) в этом случае согласно [1] примет вид
![]() , (12)
, (12)
где ![]() – плазменная частота. Величина
– плазменная частота. Величина ![]() определяется известным [1] равенством
определяется известным [1] равенством
![]() , (13)
, (13)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() – электрическая постоянная, заряд и масса электрона, их концентрация.
– электрическая постоянная, заряд и масса электрона, их концентрация.
Соотношению (12) отвечают две различающиеся знаком моды (4) и кривые (7):
![]() ,
, ![]() , (14)
, (14)
поэтому волновая функция имеет вид (9), а интегродифференциальное уравнение волны (5) для обеих мод принимает единый вид дифференциального уравнения Клейна-Гордона
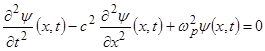 . (15)
. (15)
В качестве числового параметра неоднородности такой плазмы удобно выбрать концентрацию электронов, то есть ![]() , тогда равенство (10) с учетом (12)-(14) примет вид:
, тогда равенство (10) с учетом (12)-(14) примет вид:
![]() . (16)
. (16)
Используя этот параметр, можно описать, как рабочая область должна быть заполнена плазмой, чтобы информационный сигнал с пространственно-частотным разделением распространялся со скоростью ![]() . Для этого удобно ввести функцию
. Для этого удобно ввести функцию ![]() , значение которой равно концентрации электронов (16) в точке
, значение которой равно концентрации электронов (16) в точке ![]() рабочей области. В любом случае эта функция не зависит от переменной
рабочей области. В любом случае эта функция не зависит от переменной ![]() и строится по заданной функции пространственно-частотного разделения
и строится по заданной функции пространственно-частотного разделения ![]() . Если
. Если ![]() имеет линейный вид (11), то получим:
имеет линейный вид (11), то получим:
![]() . (17)
. (17)
Для вакуума (![]() ,
, ![]() ) уравнение (15) сводится к волновому. Оно описывает электромагнитное поле без дисперсии, естественная риманова геометрия которого является псевдоевклидовой с предельной скоростью движения, равной
) уравнение (15) сводится к волновому. Оно описывает электромагнитное поле без дисперсии, естественная риманова геометрия которого является псевдоевклидовой с предельной скоростью движения, равной ![]() [3; 7]. При
[3; 7]. При ![]() возникает дисперсия, и можно считать, что плоские монохроматические бегущие волны с разной частотой имеют псевдоевклидову естественную геометрию, различающуюся предельной скоростью движения, которая интерпретируется как фазовая скорость волны. Далее можно отождествлять псевдоевклидову метрику волны данной частоты с псевдоевклидовой метрикой пространственно-временного континуума, в котором распространяется эта волна, что согласуется с выдвинутой в [3] гипотезой об иерархической гиперконтинуальной структуре мирового физического пространства-времени (гипотеза гиперконтинуума). Понятие пространственно-временного гиперконтинуума впервые введено в [7] в результате совместного изучения алгебраической и геометрической структур коммутативных алгебр с единицей, элементами которых являются функции синусоидальных волн. Гипотеза является отправной точкой научных исследований, направленных на обобщение представлений о структуре пространства и времени в русле перехода от современной квантовой научной парадигмы к новой системной, одновременно конструктивно соединяющей в своих рамках непрерывность и дискретность, динамичность и статичность, а также глобальность и локальность [5]. Иерархичность гиперконтинуума ограничивает применимость общепринятого принципа геометризации в физике и связанных с ним идей симметрии в геометрии за счет введения в теоретическую физику идей иерархичности [6; 8-12; 14-15], эффективность которых уже апробирована нами в рамках информатики при создании эталонной модели защищенной автоматизированной системы (ЭМЗАС) и математического аппарата ЭМЗАС-сетей [4].
возникает дисперсия, и можно считать, что плоские монохроматические бегущие волны с разной частотой имеют псевдоевклидову естественную геометрию, различающуюся предельной скоростью движения, которая интерпретируется как фазовая скорость волны. Далее можно отождествлять псевдоевклидову метрику волны данной частоты с псевдоевклидовой метрикой пространственно-временного континуума, в котором распространяется эта волна, что согласуется с выдвинутой в [3] гипотезой об иерархической гиперконтинуальной структуре мирового физического пространства-времени (гипотеза гиперконтинуума). Понятие пространственно-временного гиперконтинуума впервые введено в [7] в результате совместного изучения алгебраической и геометрической структур коммутативных алгебр с единицей, элементами которых являются функции синусоидальных волн. Гипотеза является отправной точкой научных исследований, направленных на обобщение представлений о структуре пространства и времени в русле перехода от современной квантовой научной парадигмы к новой системной, одновременно конструктивно соединяющей в своих рамках непрерывность и дискретность, динамичность и статичность, а также глобальность и локальность [5]. Иерархичность гиперконтинуума ограничивает применимость общепринятого принципа геометризации в физике и связанных с ним идей симметрии в геометрии за счет введения в теоретическую физику идей иерархичности [6; 8-12; 14-15], эффективность которых уже апробирована нами в рамках информатики при создании эталонной модели защищенной автоматизированной системы (ЭМЗАС) и математического аппарата ЭМЗАС-сетей [4].
Заключение
Возможность передачи информации со сверхсветовой скоростью через неоднородную среду вообще и неоднородную плазму, согласно (16)-(17) в частности, мы выдвигаем в качестве гипотезы, требующей экспериментальной проверки, причем ее подтверждение стало бы одним из подтверждений гипотезы о гиперконтинууме. Подтверждение гипотезы о гиперконтинууме способно открыть принципиально новые перспективы развития науки и техники.
Рецензенты:
Белокуров С.В., д.т.н., доцент, начальник кафедры математики и естественно-научных дисциплин ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж;
Душкин А.В., д.т.н., доцент, начальник кафедры управления и информационно-технического обеспечения ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж.
Библиографическая ссылка
Дубровин А.С., Хабибулина С.Ю. ПЕРЕДАЧА ИНФОРМАЦИИ В ДИСПЕРГИРУЮЩЕЙ ЛИНЕЙНОЙ СРЕДЕ И ВОЛНЫ В ПРОСТРАНСТВЕННО-ВРЕМЕННОМ ГИПЕРКОНТИНУУМЕ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17301 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/spno.121-17301



