В целях обеспечения безопасного и устойчивого развития страны в условиях изменяющегося климата принята Климатическая доктрина Российской Федерации, что указывает на актуальность развития научной основы политики в области климата.
В формировании климатической изменчивости важная роль принадлежит изменчивости циркуляции атмосферы. Глобальная атмосферная циркуляция является одним из механизмов, определяющих все многообразие региональных особенностей климата. Основным звеном атмосферной циркуляции Северного полушария является циркумполярный вихрь (ЦПВ) с центром в районе полюса и западно-восточным движением воздуха. Его характеристики существенно влияют на формирование и распределение аномальных погодных условий. Поэтому надежное метеорологическое обеспечение оперативной и плановой деятельности потребителей метеорологической информации невозможно без всестороннего изучения внутренней структуры этой компоненты общей циркуляции атмосферы.
Цель работы – совершенствование моделей климатической системы и прогностических схем за счет выявления и учета структурных особенностей ЦПВ Северного полушария.
Для достижения поставленной цели решается задача так называемого разведочного статистического анализа [1], позволяющего выявить вероятностную и геометрическую природу типового метеорологического материала – многомерных данных барической топографии. При этом используются методы факторного, кластерного, дискриминантного анализа.
Исходная информация. В качестве исходного материала использовались данные реанализа параметров атмосферы NCEP/DOEAMIP-II [6] по Северному полушарию. Рассматривались значения геопотенциальной высоты Н500(на изобарическом уровне 500 гПа) в узлах регулярной широтно-долготной сетки с шагом 2,5о по срокам 00, 06, 12, 18 час. (Всемирного скоординированного времени) за период 1979–2013 гг. По срочным данным геопотенциальной высоты проведен расчет среднесуточных значений. Задача решалась для центрального зимнего месяца (января), когда циклонический характер ЦПВ наиболее выражен.
Используемая модель ЦПВ. При построении математической модели ЦПВ выбран подход [2–4], определяющий аналогию между проекцией поверхности Н500 на плоскость XOY и двумерным нормальным распределением на этой плоскости случайных величин X, Yс весами pij для точек (xi, yj). При этом веса проекций элементов объема «чаши», образованной топографией изобарической поверхностии горизонтальной плоскостью, проходящей через краевую изогипсу Hо, определяются по формуле [4]:
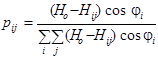 , (1)
, (1)
где Hij - значение высоты изобарической поверхности в узле (xi, yj); ji - широта точки (xi, yj); учитываются только точки (узлы), для которых выполняется условие Hij<Hо.
В декартовой системе координат XOY центр совмещен с географическим полюсом, ось X направлена на юг вдоль гринвичского меридиана, ось Y – на восток (90о западной – 90о восточной долготы). В этой системе центр циркуляции (xc, yc) определяется как центр масс системы материальных точек.
Характеристиками модели циркумполярного вихря являются: площадь S, ограниченная с юга изогипсой Hо; условная «масса» М рассматриваемого объема; условная плотность ЦПВz = М/S; геометрические параметры концентрации двумерного распределения около центра масс: угол q между главной осью эллипса рассеяния и осью X; su, sv – полуоси или главные средние квадратические отклонения эквивалентного единичного эллипса рассеяния; коэффициент сжатия эллипса k = σv / σu[2-4].
Используемая модель ЦПВ [2–4] программно реализована для поверхности H500. В качестве краевой изогипсы Hо выбрана характерная для января изогипса, совпадающая с осью планетарной высотной фронтальной зоны, Hо= 540 дам [2].
Кластерный анализ. С целью определения однородных по структуре групп множества циркумполярных образований{Оi}(i =1, 2, …, n; где n – объем выборки суточных значений характеристик ЦПВ, n=1085) с описательными признаками xij(j = 1, 2, …,p; к расчету приняты параметры модели вихря: xc, yc,S, M, z, θ, σu, σv,k), проведена процедура иерархической кластеризации объектов многомерного пространства. При этом не требуется априорной информации о распределении генеральной совокупности [1]. Мерой близости, «похожести» различных объектов Оl, Оm выбрано хеммингово расстояние («городских кварталов») [1]:
![]() . (2)
. (2)
Предварительно проведена стандартизация параметров по формуле ![]() , чтобы компоненты вектора признаков были однородны по своему физическому смыслу. Для меры (2) влияние отдельных больших разностей (выбросов) уменьшается, так как они не возводятся в квадрат как в евклидовой метрике.
, чтобы компоненты вектора признаков были однородны по своему физическому смыслу. Для меры (2) влияние отдельных больших разностей (выбросов) уменьшается, так как они не возводятся в квадрат как в евклидовой метрике.
Дерево иерархической кластеризации имеет три отчетливо выделяющиеся ветви. Таким образом, при рассмотрении среднесуточных характеристик циклонических образований можно говорить, в первом приближении, о трех группах (типах) ЦПВ. При этом объекты циркуляции 1-го типа составляют 30,1 % случаев, 2-го – 29,6 %, 3-го – 40,3 %.
В таблице 1 сведены статистические оценки основных характеристик ЦПВ отмеченных кластеров. Из данных таблицы 1 видно, что объекты циркуляции 3-го кластера, в сравнении с объектами кластеров 1, 2, имеют в среднем большую «массу» и «плотность», более сжатый эллипс рассеяния масс. Выявлена особенность распределений угла ориентации эллипса рассеяния по кластерам: для кластера 1 (в основном) θ> 0; для кластера 2 – θ< 0 (т. е. объекты циркуляции кластера 1 имеют направление главной оси эллипса рассеяния восточной ориентации, а кластера 2 – западной); для кластера 3 угол q имеет бимодальное распределение.
Таблица 1
Статистические оценки параметров ЦПВ по кластерам (500 гПа, январь)
|
Параметр ЦПВ |
Кластер 1 |
Кластер 2 |
Кластер 3 |
|||
|
средняя |
ср.кв. откл. |
средняя |
ср.кв. откл. |
средняя |
ср.кв. откл. |
|
|
xс, км |
-420,02 |
394,43 |
-552,63 |
330,64 |
-503,71 |
284,68 |
|
yс, км |
-91,15 |
328,29 |
-59,09 |
326,82 |
27,47 |
264,89 |
|
S*10-6, км2 |
63,39 |
3,83 |
65,34 |
3,32 |
65,57 |
2,92 |
|
M*10-9, км2дам |
1,37 |
0,16 |
1,38 |
0,17 |
1,56 |
0,15 |
|
z, дам |
21,72 |
2,54 |
21,19 |
2,71 |
23,86 |
2,42 |
|
θ, град. |
32,34 |
14,34 |
-31,98 |
17,75 |
2,80 |
31,80 |
|
σu, км |
2453,85 |
147,77 |
2411,18 |
127,15 |
2217,08 |
119,02 |
|
σv, км |
1617,53 |
138,59 |
1688,51 |
143,82 |
1788,39 |
129,93 |
|
k |
0,66 |
0,07 |
0,70 |
0,07 |
0,81 |
0,07 |
Факторная модель ЦПВ. С целью сжатия информации и определения структуры данных проведен факторный анализ, позволяющий обнаружить скрытые факторы, объясняющие связи между наблюдаемыми признаками объекта. В факторном анализе применяется модель описания переменных Хj(j = 1, 2, …, p) линейной комбинацией r ненаблюдаемых факторов f1, f2,…,fr, при этом r < p:
Х*j= aj1.f1 + aj2f2 + … +ajr. fr + ej, (3)
где Х*j – центрированные и нормализованные исходные данные; fi, i= 1, 2, …, r, называются общими факторами, так как они являются общими для представления всех признаков; ej – остаток или специфичный фактор для переменной Хj; aji – неизвестные коэффициенты, имеют специальное название – факторные нагрузки (задача факторного анализа состоит в том, чтобы оценить их некоторым оптимальным образом).
В результате факторного анализа определены общие факторы модели ЦПВ на уровне 500 гПа, объясняющие 89,5 % общей дисперсии признаков. Содержательная интерпретация факторов дана в соответствии с факторными нагрузками (после «варимакс-вращения») на параметры ЦПВ, превышающими по модулю 0,7 [1].
Первый фактор наиболее тесно связан с предикторами su, sv, k, что дает основание интерпретировать f1 как фактор формы рассеяния условных масс ЦПВ (объясняет 28,9 % общей дисперсии признаков).
Фактор f2, судя по нагрузкам на параметры M, z, можно назвать фактором массы ЦПВ (объясняет 24,0 % общей дисперсии).
Соответственно другим факторам даны следующие интерпретации:
- f3 – фактор положения центра вихря (15,7 % общей дисперсии);
- f4 – фактор ориентации эллипса рассеяния (11,3 % общей дисперсии);
- f5 – фактор площади вихря (9,6 % общей дисперсии).
На рисунках 1–3 объекты выделенных кластеров представлены в разных проекциях: на плоскости факторов f1, f2 (рисунки 1, 2) и f1, f4 (рисунок 3).
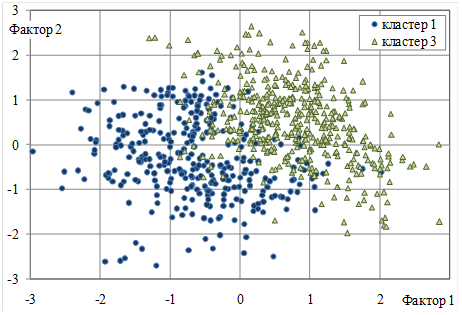
Рис.1. Распределение объектов ЦПВ на плоскости факторов f1, f2 с маркировкой групп, полученных кластеризацией (без объектов кластера 2)
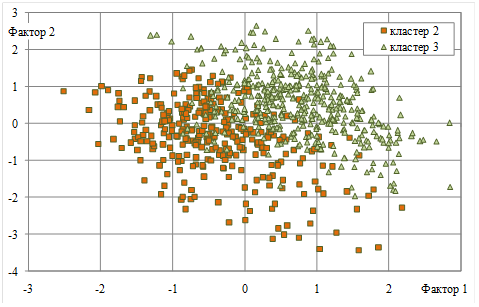
Рис.2. Распределение объектов ЦПВ на плоскостифакторов f1, f2 с маркировкой групп, полученных кластеризацией (без объектов кластера 1)
Как показано на рисунках, «сгустки» объектов ЦПВ полученных кластеров выделяются визуально (чтобы не затенять картину отличия скоплений объектов определенных групп, на каждом рисунке не показаны объекты одного из кластеров).
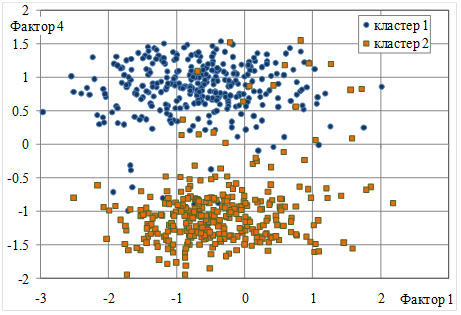
Рис.3. Распределение объектов ЦПВ на плоскостифакторов f1, f4 с маркировкой групп, полученных кластеризацией (без объектов кластера 3)
Оценка однородности кластеров. В целях определения однородности групп, проведена проверка гипотезы о принадлежности факторов рассматриваемых кластеров одним и тем же распределениям. Использовались непараметрические методы (или свободные от распределения): на основе критериев Колмогорова – Смирнова и рангового Манна – Уитни[6], – не требующие предпосылки существования закона распределения.
В таблице 2 представлены результаты оценки по совокупности двух указанных критериев статистического различия распределений соответствующих факторов в рассматриваемых группах на уровне значимости α = 0,05 (знаком «+» отмечены случаи принятия статистической гипотезы, что две совокупности имеют одно и то же распределение; знаком «-» –принятия альтернативной гипотезы).
Таблица 2
Оценки статистического различия распределений факторов в кластерах (α= 0,05)
|
Кластеры |
f1 |
f2 |
f3 |
f4 |
f5 |
|
1, 2 |
– |
+ |
+ |
– |
– |
|
1, 3 |
– |
– |
– |
– |
– |
|
2, 3 |
– |
– |
+ |
– |
+ |
Как следует из данных таблицы 2, существенно различаются распределения всех факторов в кластерах 1, 3; в кластерах 1, 2 различаются только распределения факторов f1, f4, f5; в кластерах 2 и 3 – f1, f2, f4.
На рисунке 4 даны в сравнении статистические характеристики факторов по группам (мода, 50-ти процентный интервал и размах варьирования), графическое представление которых визуально подтверждает данное утверждение.
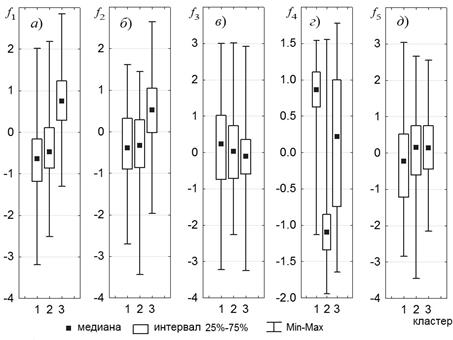
Рис. 4. Сравнение для выделенных кластеров статистических характеристик факторов: а) f1; б) f2; в) f3; г) f4; д) f5
Дискриминантный анализ. Для выяснения, какие факторы вносят свой вклад в дискриминацию между полученными совокупностями объектов ЦПВ, в задаче использовался дискриминантный анализ. В результате дискриминантного анализа, во-первых, построены классификационные функции, предназначенные для определения того, к какой группе наиболее вероятно может быть отнесен отдельный объект. Во-вторых, определены дискриминантные функции, разделяющие возникающие совокупности.
Каждой группе (совокупности объектов) соответствует своя классификационная функция dci(i = 1, 2, 3), определяемая вектором коэффициентов и константой:
dc1 =–2,734– 1,663f1– 0,808f2 + 0,396f3+1,779f4– 0,692 f5, (4)
dc2 = –2,726– 0,999f1– 0,986f2+ 0,056f3– 2,212f4+ 0,178 f5, (5)
dc3 = –2,079 + 1,979f1+1,329f2– 0,337f3 + 0,294f4+ 0,387f5, (6)
Данные функции классификации (14)–(16) можно использовать для прямого вычисления показателя классификации для некоторых новых значений. Наблюдение (объект циркуляции) считается принадлежащим той совокупности, для которой получен наивысший показатель классификации.
В результате проведенного анализа определены дискриминантные функции d1 и d2. Функция d1 в основном дискриминирует между группой 3 и объединением групп 1 и 2. Функция d2 дискриминирует между группой 1 и 2. По коэффициентам полученных дискриминантных функций, представленных в стандартизованном виде:
d1 = – 1,004f1– 0,781f2+ 0,226f3– 0,070f4– 0,267f5, (7)
d2 = – 0,095f1+ 0,125 f2+ 0,101f3 + 1,001f4– 0,281f5, (8)
можно судить о степени влияния каждого предиктора на дискриминацию групп. Так, согласно (7), (8), наибольшее влияние на дискриминацию между группой 3 и совокупностью групп 1, 2 оказывают факторы f1 и f2 (формы и массы ЦПВ); на дискриминацию между группами 1 и 2 наибольшее влияние оказывает фактор f4 (ориентации эллипса рассеяния условных масс ЦПВ), что подтверждает и распределение объектов на рисунках 1–3.
Другой целью применения дискриминантного анализа является проведение классификации. Если модель установлена и получены дискриминирующие функции, возникает вопрос о том, как хорошо они могут предсказывать, к какой совокупности принадлежит конкретный объект циркуляции. Такой анализ не проводился, поскольку это цель следующего этапа – модельного дискриминантного анализа. Цель разведочного анализа – предварительная оценка внутренней структуры исходной совокупности.
Достоверность полученных результатов подтверждается большим объемом данных, привлеченных для исследования, и применением классических методов статистической обработки информации.
Полученные результаты позволяют говорить о дифференцированном использовании данных о состоянии ЦПВ в разрабатываемых погодно-климатических моделях, тем самым повысить эффективность метеорологического обеспечения.
Рецензенты:
Куролап С.А., д.г.н., профессор, заведующий кафедрой геоэкологии и мониторинга окружающей среды, ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж;
Кузнецов И.Е., д.т.н., начальник13 кафедры гидрометеорологического обеспечения, ФГБОУ ВПО «Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина» Министерства обороны Российской Федерации, г. Воронеж.
Библиографическая ссылка
Шипко Ю.В., Шувакин Е.В. ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ ЦИРКУМПОЛЯРНОГО ВИХРЯ СЕВЕРНОГО ПОЛУШАРИЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17282 (дата обращения: 12.03.2026).



