Цель исследования. Как было показано в работах [2-3], размер растянутой зоны перед образованием трещин сильно зависит от коэффициента упругости растянутого бетона, который заметно различается для разных классов и видов бетонов, что в расчётных формулах непосредственно никак не учитывается. Поэтому точность определения расстояния между трещинами и, соответственно, ширины их раскрытия невысока, что обусловливает необходимость применения иных расчётных схем.
Материал и методы исследования. Во всех не сугубо эмпирических, а достаточно известных расчётных методах, имеющих определённый физический смысл [4 - 6, 9], основной недостаток состоит в том, не учитывается влияние напряжённого состояния сжатой зоны в сечении с трещиной на напряжения в середине расстояния между первичными трещинами. В этом отношении физически наиболее соответствует сути задачи определения расстояния между трещинами блочная модель, сформулированная в [7]. Модель В.И. Мурашёва [5], лежащая в основе большинства современных моделей, по существу тоже блочная, но в ней рассматривается только часть блока, примыкающая к растянутой арматуре, в отрыве от сжатой части блока, под которым понимается часть конструкции между смежными нормальными трещинами. Этот же недостаток присущ и методу расчёта, заложенному в нормы проектирования (СП 63.13330.2012), где в формуле для базового расстояния между трещинами присутствуют только элементы растянутой зоны (площадь сечения растянутого бетона, площадь сечения растянутой арматуры, её номинальный диаметр).
Всё это не отражает физику явления. А она состоит в том, что после образования начальных трещин конструкция представляет собой систему блоков, разделённых трещинами и связанных между собой сжатой зоной и растянутой арматурой [7]. В случае неармированной бетонной балки, малоармированной железобетонной балки или железобетонной балки без сцепления арматуры с бетоном, в которой совместная работа арматуры и бетона обеспечивается лишь анкеровкой арматуры в торцевых частях конструкции, возможно образование только одной трещины. Тогда возникает всего два блока.
Вообще, кинетика процесса трещинообразования зависит от режима нагружения. Если нагрузка возрастает непрерывно или малыми ступенями, то сначала образуются на определённом расстоянии друг от друга в зависимости от степени армирования и качества сцепления арматуры с бетоном первичные трещины в момент, когда усилия станут равными усилиям трещинообразования. Затем по мере роста нагрузки, и соответственно усилий, первичные трещины подрастают вглубь сечения и по ширине раскрытия. В тот момент, когда напряжения в наиболее растянутых волокнах в середине сечения достигнут величины предельного сопротивления бетона растяжению, появляются промежуточные трещины. Раскрытие этих промежуточных трещин может привести даже к некоторому уменьшению ширины раскрытия трещин, образовавшихся на предыдущем этапе.
В случае, когда нагрузка прикладывается большими ступенями или целиком (хотя и без динамических эффектов), трещины образуются одномоментно и в дальнейшем картина трещинообразования меняется лишь вследствие температурно-влажностных изменений среды и перераспределения усилий между арматурой и бетоном вследствие ползучести бетона.
С учётом изложенного расчёт ширины раскрытия трещин будем рассматривать с позиций блочной модели железобетона [7] путём использования линий влияния для перемещений контурных точек прямоугольной области, соответствующей высоте сечения элемента и первоначально заданному расстоянию между трещинами. Для уточнения расстояния между трещинами применим линии влияния для нормальных напряжений на уровне контакта между бетоном и растянутой арматурой от единичных нормальных сил на торцовых гранях блока и единичных тангенциальных сил по линии контакта арматуры с бетоном.
Линии влияния для перемещений и напряжений в контурных точках прямоугольной области строятся методом конечных элементов с помощью программного комплекса ЛИРА в линейно-упругой постановке. Распределение напряжений на продолжении трещины (то есть, на торцовых гранях блока) отыскивается из решения нелинейной задачи, как в работах [8, 9] или в нормах (СП 63.13330.2012).
Результаты исследования и их обсуждение. Матрица │Lu(Ni=1,γ,k,i)│ размером n*n представляет собой значения линий влияния для перемещений точек k=1, 2,..., n торцовых граней блока с соотношением сторон γ=lcrc/h0=(8; 4; 2; 1; 0,5; 0,25) от единичных сил Ni , нормально приложенных к тем же торцовым граням х=±lcrc/2 последовательно в точках i=1,2, 3,...,n:
│Lu(Ni=1,γ,k,i)│= 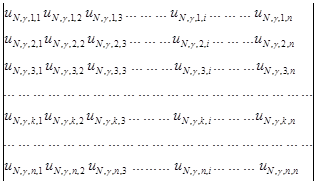 . (1)
. (1)
Матрица размером n*m │Lu(Tj=1,γ,k,j)│ представляет собой значения линий влияния для перемещений точек k=1, 2,...n торцовых граней блока с соотношением сторон γ=lcrc/h0=(8; 4; 2; 1; 0,5; 0,25) от единичных сил Tj , тангенциально приложенных к нижней грани y=h0 последовательно в точках j=1,2, 3,...,m:
│Lu(Tj=1,γ,k,j)│= 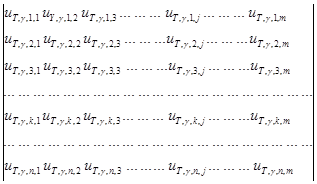 . (2)
. (2)
Перемещение k - той точки контура х=±lcrc/2 при действующих нагрузках, которые приведены к узловым Ni , Tj , определяется выражением
uk(γ)= 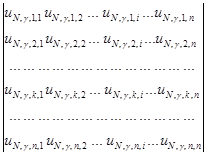 *
*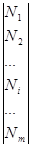 +
+ 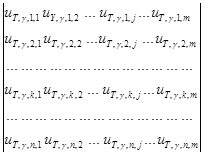 *
*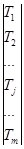 (3)
(3)
или в свёрнутом виде
uk(γ)=│Lu(Ni=1,γ,k,i)│*│Ni│+│Lu(Tj=1,γ,k,j)│*│Tj│= 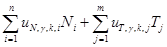 = , k=1,2,...n. (4)
= , k=1,2,...n. (4)
Пусть, например, при некотором уровне загружения конструкции и сформировавшейся совокупности трещин с γ=1 напряжения на продолжении трещины заменены вектором │Ni│, а усилия сцепления по контакту арматуры с бетоном заменены вектором │Tj│. Схема деформированного блока с действующими усилиями показана на рисунке 1.
По формулам (3) или (4) определяются перемещения всех узловых точек торцовых граней блока. В пределах сжатой зоны все перемещения уложатся согласно гипотезе плоских сечений на линию, которая сместится внутрь блока, поскольку в сжатой части размеры блока в результате деформации уменьшатся. В пределах растянутой зоны, где по берегам трещины напряжения, а значит, и узловые нагрузки, отсутствуют, узловые точки сместятся наружу блока из-за деформации растяжения блока между трещинами. Однако, если линию контакта смежных блоков, т. е. линию сжатой зоны, продолжить до крайнего растянутого волокна, то смещения точек контура в растянутой части блока не «дотянут» до линии, продолжающей контур сжатой зоны:
uq<u1-(u1/x)yq, (5)
где q - номер узла на продолжении линии (точнее, поверхности) сжатой зоны; yq - расстояние этого узла от крайнего волокна сжатой зоны; u1 - смещение узла, расположенного в крайнем сжатом волокне; x - высота сжатой зоны.
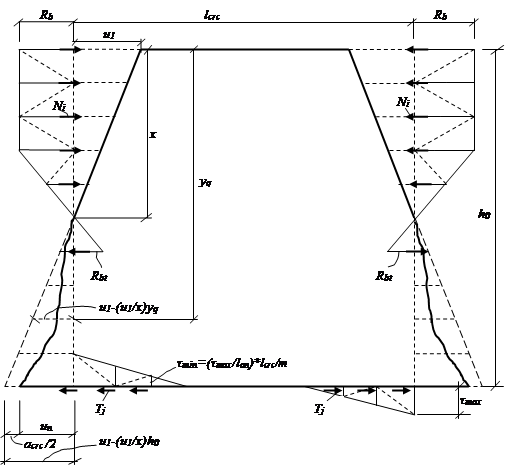
Рис.1. Схема деформирования блока с трещинами
Как видно из рис. 1, разность, составленная из правой и левой частей неравенства(5), определяет половину ширины раскрытия трещины, вторая половина которой относится к соседнему блоку, не показанному на рисунке:
acrc,q=2[u1-(u1/x)yq-uq], (6)
где q=r, r+1, r+2,...,n - нумерация узлов в области трещины.
При q=n имеем значение половины ширины раскрытия трещины на уровне арматуры
Заметим, что из схемы рисунка 1 легко получить выражение кривизны элемента. В самом деле, отношение перемещения крайнего узла сжатой грани u1 к высоте сжатой зоны х составляет u1/х=tg(α/2) или с учётом малости линейных и угловых величин деформаций
u1/х=α/2, (7)
где α - угол взаимного поворота торцовых сечений блока вследствие деформации
α=lcrc/ρ, (8)
ρ - радиус кривизны блока.
Сопоставив выражения (7) и (8), получим кривизну блока, соответствующую рассматриваемому напряжённо-деформированному его состоянию
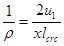 . (9)
. (9)
Необходимо отметить, что, строго говоря, задавая, как изложено выше распределение напряжений на продолжении трещины, например, в виде трапеции, прямоугольника или треугольника, мы не получим в сжатой зоне чёткой линии, на которую уложатся перемещения всех узловых точек. Будет иметь место некоторая «депланация» сечения, потому что задаваемое распределение напряжений является результатом приближённого решения задачи, в основе которой лежит система уравнений, составленных на условии линейности распределения относительных деформаций, а не перемещений. В книге же [8] показано, что распределение напряжений при условии линейности перемещений получается нелинейным. Однако отклонения перемещений узловых точек от прямой линии в пределах сжатой зоны (линии контакта смежных блоков) пренебрежимо малы по сравнению с отклонениями узловых точек от продолжения линии контакта в область раскрытия трещины.
Рассмотрим конкретный расчёт железобетонной балки прямоугольного поперечного сечения b*h0=0,25*05 м2 из бетона класса В20, армированной в растянутой зоне тремя стержнями арматурной стали диаметром 28 мм класса А400 общей площадью поперечного сечения 18,47 см2. Усилие, действующее в наиболее нагруженном сечении 268 кНм. Методом, изложенным в [8-10] с использованием двухзвенной кусочно-линейной диаграммы бетона при сжатии, найдём усилие в растянутой Ns=648 кН , вектор узловых нормальных усилий в сечении с трещиной
Ni=│93,75; 187,5; 187,5; 187,5; -8,44; 0; 0; 0; 0; 0; 0│,
а задавшись по рекомендациям норм (СП 63.13330.2012) эпюрой сцепления между арматурой и бетоном в пределах зоны анкеровки, как показано на рис. 1, найдём вектор узловых тангенциальных усилий
Tj=│37,8; 60,8; 45,6; 30,4; 15,2│.
Варьирование значений γ=lcrc/h0=│8; 4; 2; 1; 0,5; 0,25│ показывает, что
функция σ0(γ) пересекает линию σ0(γ)=Rbt,ser при γ=1,1. Поэтому воспользуемся матрицей линий влияния для перемещений контурных точек торцовых граней при γ=1:
uk(γ)=│Lu(Ni=1,γ=1,k,i)│*│Ni│+│Lu(Tj=1,γ=1,k,j)│*│Tj│=
= , 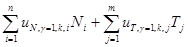 k=1,2,...,n, n=11, m=5. (10)
k=1,2,...,n, n=11, m=5. (10)
Результаты вычислений по формуле (5) представлены на рис. 2.
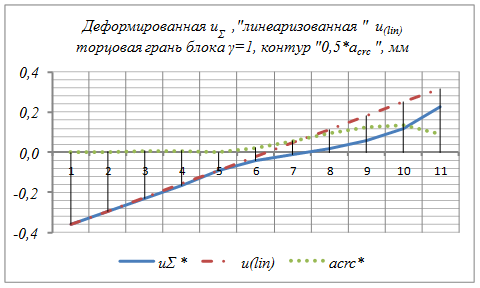
Рис. 2. Деформированный контур «uΣ» торцовой грани блока γ=1; «линеаризованный» контур u(lin) торцовой грани, полученный продолжением линии контакта блоков в зоне сжатия до растянутой грани; полуширина раскрытия трещины 0,5acrc=u(lin)-uΣ
Линия деформированного контура uΣ торцовой грани блока γ=1 от нормальных напряжений на продолжении трещины и усилий сцепления арматуры с бетоном - почти прямая на участке контакта смежных блоков, то есть, от узла 5, в котором находится вершина трещины, до узла 1 в крайнем сжатом волокне сечения. «Почти прямая» в том смысле, что узлы 2, 3 и 4 имеют отклонения от прямой, соединяющей 1-й и 5-й узлы, очень малые по сравнению с отклонениями узлов 6 - 11 от прямой 1 - 5, продолженной до растянутой грани. Малые отклонения узлов 2-4 от прямой 1-5 обусловлены погрешностями линий влияния, а большие отклонения узлов 6-11 от продолжения прямой 1-5 в область раскрытия трещины обусловлены отсутствием напряжений на берегах трещины.
Уравнение линеаризованного контура торцовой грани
ui(lin)=u1-(u1-u5)/(5-1)*(i-1), i=1,2,...,11. (11)
Разность значений (11) и (10) определяет половину ширины раскрытия трещины:
ui(lin)-(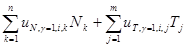 )=0,5acrc,i.
)=0,5acrc,i.
Как видно из рисунка 2, полуширина раскрытия трещины на уровне контакта с арматурой составляет 0,105 мм. Значит, раскрытие трещины равно 0,21 мм:
acrc=2*(ui(lin)-( 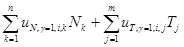 ))=0,21 мм.
))=0,21 мм.
Кривизна элемента с трещинами по формуле (9): 1/ρ=0,0027 м-1.
Следует отметить важную особенность изложенного метода определения ширины раскрытия трещин: он позволяет рассчитать форму трещины по всей её длине. В данном случае форма получилась параболической с максимумом на удалении от растянутой грани и уменьшением приращения раскрытия к крайнему растянутому волокну. Это напоминает «веретенообразные» трещины, о которых, как о возможной форме раскрытия, речь шла в книге [8]. Здесь наибольшее раскрытие получилось в 10 - м узле: acrc=2*0,145=0,29 мм. В случае одиночных трещин (при относительно невысоком уровне загружения, слабом сцеплении бетона с арматурой или большом γ, например, при γ=8), форма трещины близка к гиперболической с увеличением приращения раскрытия к крайнему растянутому волокну.
По методике норм (СП 63.13330.2012) напряжение σs в арматуре, соответствующее рассматриваемому напряжённому состоянию, получается равным 362 МПа, базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами ls - равным 0,428 м (γ=lcrc/h0=0,856), ширина кратковременного раскрытия трещин acrc=0,000356 м≈0,36 мм и кривизна 0,00346 м-1.
Заключение
1. Ширина раскрытия трещины, определённая изложенным способом, меньше определённой по нормам на 24%, кривизна - меньше на 28%. Это объясняется тем, что в изложенном способе линии влияния позволяют вычислить только упругие деформации, хотя напряжения на торцовых гранях блоков вычислены с использованием нелинейных диаграмм деформирования бетона. Введение корректирующего коэффициента, равного соответствующему стадии нагружения конструкции, сближает результаты расчёта деформаций по изложенному способу и по СП 63.13330.2012 до разницы, не превышающей в рассмотренной задаче 10%.
2. Изложенный способ расчёта раскрытия трещин имеет преимущество перед нормативным методом, состоящее в том, что в отличие от нормативного метода, определяющего ширину раскрытия трещины в одной точке, он даёт ширину раскрытия трещины по всей её длине. В некоторых случаях, когда речь идёт не только о защите арматуры от коррозии, а и о защите от ионизирующих излучений, коррозии бетона, это преимущество может оказаться важным.
Рецензенты:
Гарагаш Б.А., д.т.н., профессор, генеральный директор ЗАО «Инвестиционно-Строительная Компания «Милбор»», г Сочи;
Макаров К.Н., д.т.н., профессор, заведующий кафедрой «Строительство», ФГБОУ ВПО "Сочинский государственный университет" Министерство образования и науки Российской Федерации, г. Сочи.
Библиографическая ссылка
Иваненко А.Н., Иваненко Н.А., Пересыпкин Е.Н. РАСЧЁТ РАСКРЫТИЯ ТРЕЩИН И КРИВИЗНЫ ИЗГИБАЕМЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ НА ОСНОВЕ БЛОЧНОЙ МОДЕЛИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17260 (дата обращения: 12.03.2026).



