Механика кровотока и перенос веществ (медикамента) в организме находятся в центре внимания многих исследователей на протяжении достаточно большого времени. Наряду с переносом вещества по кровеносной системе, происходит и перенос информации. Конечно, поток крови имеет большое значение для многих процессов, происходящих в каждом живом организма. В частности, процессы, связанные с вопросом транспорта (переноса), представляют большой интерес для многих приложений в области физиологии и медицины. Есть много возможностей для вещества проникновение в обращении: вдохновение, метаболическая активность, эндокринной контроля, кишечные поглощения, инъекции лекарств и других. В зависимости от свойств различных веществ могут вызывать различные воздействия на организм или его частей.
В работе [1] описывается история развития и рассматривается задача численного моделирования функционирования замкнутой сердечно-сосудистой и дыхательной систем организма человека с учетом их взаимодействия и переноса веществ. Эта задача является актуальной, поскольку болезни, связанные с нарушением функции сердечно-сосудистой системы, уверенно лидируют среди главных причин смертности во всем мире. Для определения процедуры доставки лекарств в патологических ситуациях применяются численное моделирование и моделирование наркотиков транспорта в кровоток и через окружающие ткани [2]. А во многих работах также исследуются и моделируются процессы, связанные с переносом веществ в организме человека.
В данной работе рассматривается численный метод для распространения медикамента после его инъекции в сосуд по математическому моделированию. И также предложен метод моделирования распространения веществ в тканях, окружающих сосуды.
Постановка задачи
В качестве основы для замкнутой модели, описывающей кровообращение в простом виде, предлагается использовать квазиодномерную нелинейную модель постоянного течения вязкой несжимаемой жидкости по эластичной трубке. В качестве медикамента можно использоваться разные вещества (например, пептиды, которые могут проникать в клетки, яд, действие которого требуется локализовать областью пораженных тканей и др.). С помощью соответствующих граничных условий эта модель обобщается на случай постоянного потока из сердца (50 см/сек) по графу эластичных трубок.
Сосуды будут выступать в роли ребер графа, узлами графа будут точки слияния двух и более сосудов (т. н. узлы ветвления), либо сердце, органы и ткани. Для каждого сосуда давление Р, скорость U и площадь поперечном сечении любого сосуда S при рассмотрении задачи переноса медикамента будем считать известными.
В данной работе предлагалось медикамент вводятся в 30% длины 2-ого сосуда (в точке A, см. Рис.1). А проведенное время исследования составляет 250 сек. и время воздействий (введения) проводится одну минуту от 20 сек до 80 сек. Вначале моделируются процессы транспорта веществ по сосудам артерии и через мультиузел по сосудам вены. Когда медикаменты пришли в сосуд с номером 7 (в точке C), рассматривается распределение медикамента в ткани.
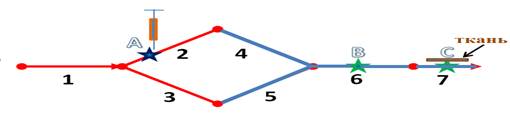
Рис.1. Модель инъекции медикамента в сосуд артерии
Модель переноса медикамента по графу сосудов и разностная задача
При численной реализации задачи о движении вязкой несжимаемой жидкости в эластичной трубке использовалась явная двухшаговая гибридная схема, соответствующая наиболее точной монотонной схеме первого порядка и наименее осциллирующей схеме второго порядка точности [3]. Для численного решения поставленной задачи воспользуемся методом конечных разностей. Введем на каждом сосуде равномерную сетку ωh = {xP= ph, p = 1,..., N} где h – шаг по расстоянии. Шаг по времени (τ) будем считать постоянным. Вместо функций непрерывного аргумента С, U, S будем рассматривать их сеточные аналоги с, u, s. В работе построены разностные приближения всех условий задачи.
В работе [1]течение крови в каждом сосуде описывается системой уравнений гемодинамики, в которой выполняются законы сохранения массы и импульса, и их соответствующие граничные условия.
Концентрация j-го медикамента Сjс учетом переноса кровью и при наличии источников удовлетворяет дифференциальному уравнению [4]
![]() (1)
(1)
где ![]() —удельная концентрация j-го медикамента в k-й трубке;
—удельная концентрация j-го медикамента в k-й трубке; ![]() —источник или сток массы;
—источник или сток массы; ![]() — скорость крови;
— скорость крови; ![]() —коэффициент, регулирующий конвективный перенос медикамента (для растворенных в плазме крови веществ
—коэффициент, регулирующий конвективный перенос медикамента (для растворенных в плазме крови веществ ![]() = 1, для макромолекул и форменных элементов 0 ≤
= 1, для макромолекул и форменных элементов 0 ≤ ![]() < 1).
< 1).
В данной работе уравнение (1) определяется
![]() (2)
(2)
![]() (2-a)
(2-a)
![]() (3)
(3)
![]() (3-a)
(3-a)
где ![]() и
и ![]() — удельная концентрация медикамента (плазмы и эритроциты соответственно) в трубке ; t — время; x —длина сосуда; α — интенсивность обмена между плазмой и эритроцитами.
— удельная концентрация медикамента (плазмы и эритроциты соответственно) в трубке ; t — время; x —длина сосуда; α — интенсивность обмена между плазмой и эритроцитами.
А для обмена медикамента между плазмой и тканей, концентрация которых в рамках одномерного приближения полагается одинаковой во всем сосуде, а также в точках ткани, равноудаленных от стенки сосуда, уравнение (1) определяется
![]() (4)
(4)
![]() (4-a)
(4-a)
Где β — интенсивность обмена между плазмой и тканями ;![]() — концентрация медикамента в ткани, которая определяется уравнением
— концентрация медикамента в ткани, которая определяется уравнением![]() ,γ — скорость переработки медикамента в тканях.
,γ — скорость переработки медикамента в тканях.
Граничные условия для рассматриваемых уравнений должны ставиться с учетом поведения характеристических кривых на границе области интегрирования, потому что они имеют гиперболический тип. С учетом поведения его характеристики краевые условия для уравнений (2 и 3) ставятся на границах трубки, наклон которой определяется знаком линейной скорости потока. Таким образом, если скорость потока на границе трубки направлена из нее (положительна на выходе или отрицательна на входе), то постановка граничного условия не требуется, а соответствующее значение концентрации вычисляется из уравнений(2и 3).
Для постановки граничного условия на входе в кровеносную систему задана концентрация переносимого медикамента![]() :
:
![]() . (5)
. (5)
и вычислять ее из (2 и 3) при выдохе ![]() .
.
В точках ветвления кровеносных сосудов, концентрации медикамента должны быть непрерывными и определяются из уравнения (1). А концентрация медикамента первого сосуда артерии, который соединяется со сердцем, равна концентрации медикамента первого сосуда вены, который тоже соединяется со сердцем. И также в областях стыковки сосудов с камерами сердца концентрации медикамента должны совпадать с соответствующими значениями внутри камеры:
![]() , (6)
, (6)
где k= индексы трубок; Mk = номер соответствующей камеры; xk = 0 для входа в трубку и xk= Lkдля выхода. В точках стыковки трубок:
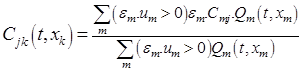 (7)
(7)
где Qm (t, xm) = Sm (t, xm) Um (t, xm); ε m = +1, x m = Lm для трубок, входящих в узел и ε m = −1, xm = 0 для исходящих из узла. Для построения аппроксимации краевых условий в узлах ветвления (условий сопряжения) будем использовать следующие приближения для условия непрерывности потоков (QE) и концентраций записываются так [5]:
![]() , (5-a)
, (5-a)
![]() . (6-a)
. (6-a)
Где
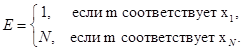
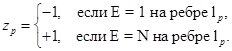
i и j —всевозможные номера ребер из Ш(т) = Ш+(т) + Ш_ (т).
Ш+(т) + Ш_ (т)—множества входящих и выходящих из вершины т ребер соответственно.
Здесь предполагается (это предположение было подтверждено вычислительными экспериментами), что в любой момент времени существует ненулевой поток медикамента, направленный из точки стыковки.
Результаты и заключение
На рис. (2-5) представлены динамика концентрации медикамента в крупных артериях и венах и распределение этого медикамента в ткани (в точке С). Как известно, основой импульс крови получает в сердце, осуществляющем насосную функцию. Профиль постоянной скорости крови для первого сосуда артерии, сосудов в точках (А и С) показан на рис.2. Концентрация медикамента в точках (А и С) представлена на рис. (3 – 5). При этом с изменением коэффициентов (α,β и γ) профиль концентрации медикамента изменяется. При увеличении значений коэффициентов (αи β) повышаются концентрация вещества в эритроците (С2) и концентрация вещества в тканях (С tissue). И с увеличением значений коэффициента (γ) уменьшается концентрация вещества в тканях.
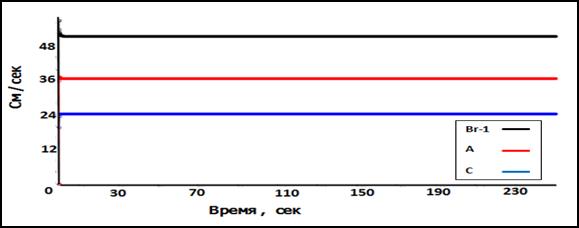
Рис.2. Скорость крови
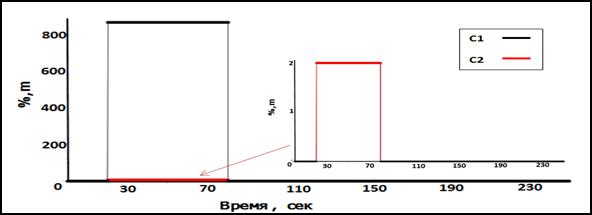
Рис.3. Концентрация медикамента в точке A(α=0,1)
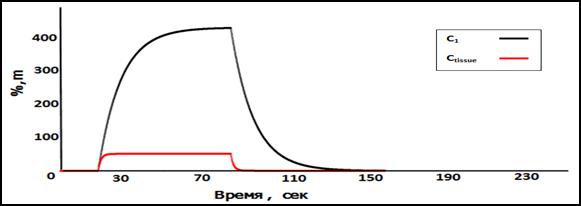
Рис.4. Концентрация медикамента в точке С (α=0,1;β=0.05;γ=0.00005)
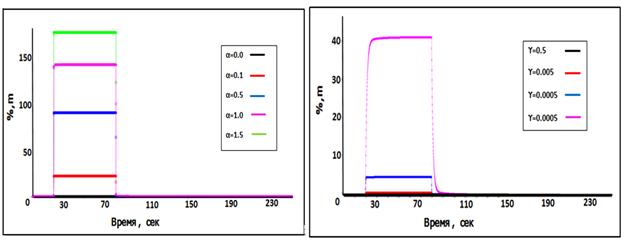
Рис.5. Концентрация медикамента в эритроците (C2 -слева) и концентрация вещества в тканях (Ctissue - справа)с различными значениями коэффициентов (α и γ)в точке С при β = 0,05.
С помощью модели можно учитывать распространения медикаментов по сосудам и в тканях, окружающих сосуд и численный анализ зоны влияния в тканях. При объединении предложенной модели с моделью глобального кровотока [1] возможен численный анализ распределения концентрации пептидов в организме после инъекции и оптимизация этого распределения с учетом расположения целевых областей.
Рецензенты:
Гагарина Л. Г., д.т.н., профессор, заведующий кафедрой «Информатика и программное обеспечение вычислительных систем» Национального исследовательского университета «МИЭТ», г. Москва.
Портнов Е.М., д.т.н., профессор кафедры «Информатика и программное обеспечение вычислительных систем», начальник научно-исследовательской лаборатории «Управляющие информационные системы» Национального исследовательского университета «МИЭТ», г.Москва.
Библиографическая ссылка
Ян Н.С., Шаньгин В.Ф. ИССЛЕДОВАНИЕ РАСПРОСТРАНЕНИЯ МЕДИКАМЕНТА В ОРГАНИЗМЕ ЧЕЛОВЕКА С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ МОДЕЛИ КРОВООБРАЩЕНИЯ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=17168 (дата обращения: 23.02.2026).



