Работоспособность технологического оборудования обеспечивается посредством согласования передаточных отношений элементов привода. Правильное определение передаточных отношений преобразующих механизмов позволяет повысить эффективность операций реализуемых при помощи технологического оборудования. Достижение данного явления возможно посредством формирования рациональной структурной схемы, как всего привода, так и отдельных его элементов. Это является актуальной задачей, решение которой возможно обеспечить посредством использования механизмов с замкнутой системой тел качения (ЗСТК) обладающих требуемыми передаточными отношениями и позволяющих реализовать сложное движение выходного звена при минимально возможном числе подвижных звеньев. Механизмы с ЗСТК обладают структурой, которая образована двумя кольцами с дорожками качения, сепаратором (водило) и телами качения с диаметрами равной или разной величины, которые могут обладать гладкими рабочими поверхностями (фрикционные) [1-10] или поверхностями с выступами (зубчатые). Механизмы рассматриваемого вида являются представителями эпициклических механизмов, следовательно, обладают тремя видами передаточного отношения: прямое, обратное и внутреннее. В зависимости от особенностей структуры связанных с сочетанием подвижных и неподвижных звеньев эпициклические механизмы данного вида являются либо планетарными, либо дифференциальными, которые могут работать в режиме редуктора (при ![]() ) или мультипликатора (при
) или мультипликатора (при ![]() ).
).
Коллектив авторов проводит исследования геометрических и кинематических параметров технологического оборудования обладающего приводом, который разработан на базе механизмов с ЗСТК с диаметрами разной (эксцентриковые) [1, 5, 8-11] или равной (соосные) [2-4, 6-7, 11] величины. В ходе исследований установлено: если структура механизма содержит замкнутую систему тел качения, то задача определения номинальных значений геометрических параметров механизмов с ЗСТК должна решаться при начальных условиях, что исходные параметры являются постоянными величинами больше нуля при наличии или отсутствии зазора между телами качения [1]. Однако дальнейшие исследования показали, что для решения задачи по определению номинальных величин геометрических параметров при данных условиях необходим ввод поправки в расчет, считая один из исходных параметров является величиной переменной. Вариация значениями радиуса тел качения и зазора не позволяет достичь требуемого результата. В этом случае получаем, что решение имеет два возможных направления ввода поправки, либо по радиусу дорожки качения наружного кольца, либо по радиусу дорожки качения внутреннего кольца. Это обстоятельство необходимо учитывать также при определении передаточных отношений механизмов данного вида. В работе [2] авторами предложен алгоритм решения поставленной задачи при ведущем внутреннем кольце и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Однако особенности геометрии механизмов с ЗСТК не позволяют полностью применить полученный алгоритм и формулы для решения рассматриваемой задачи при ведущем наружном кольце и вводе поправки по радиусу дорожки качения этого же звена.
Настоящее исследование проводится с целью дальнейшего совершенствования алгоритма определения передаточных отношений механизмов с замкнутой системой тел качения с диаметрами равной величины для любого вида симметричной структурной схемы при ведущем наружном кольце посредством ввода поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Полученные результаты позволят формировать привода технологического оборудования на базе механизмов с ЗСТК обладающих требуемыми величинами передаточных отношений.
Методы исследования, применяемые в настоящей работе, основаны на принципах кинематического анализа эпициклических механизмов при использовании положений геометрии и метода обращенного движения.
Рассмотрим ход решения задачи по определению всех видов передаточных отношений на примере планетарного механизма с ЗСТК с диаметрами равной величины при ведущем наружном кольце, неподвижном внутреннем кольце и сепараторе (водило) в качестве выходного звена, считая, что движение звеньев совершается без скольжения (проскальзывания). Для этого составим расчетную модель (рис. 1) и примем следующие обозначения: ![]() ,
, ![]() и ОВ, OН – дорожки качения и геометрические центры внутреннего и наружного колец; S – сепаратор (водило); c – зазор между телами качения;
и ОВ, OН – дорожки качения и геометрические центры внутреннего и наружного колец; S – сепаратор (водило); c – зазор между телами качения; ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() – радиусы и углы положения тел качения.
– радиусы и углы положения тел качения.
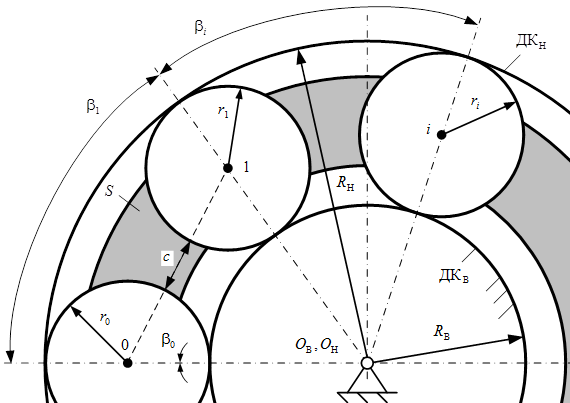
Рис. 1 Расчетная модель механизма с ЗСТК с диаметрами равной величины и зазором
В соответствии с вышеуказанной целью и выбранного вида механизма тела качения замкнутой системы имеют радиусы одинаковой величины, т. е. ![]() , тогда система начальных условий решаемой задачи имеет вид
, тогда система начальных условий решаемой задачи имеет вид
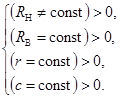 (1)
(1)
где RВ и RН – радиусы дорожек качения внутреннего и наружного колец; r и c – радиус тел качения и зазор между ними.
Следуя условию существования [9], число тел качения механизмов с ЗСТК с диаметрами равной величины и зазором найдем по формуле
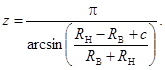 (2)
(2)
В соответствии с выбранным направлением ввода поправки в расчет номинальных величин геометрических параметров при начальных условиях системы (1) преобразование равенства (2) позволит получить формулу для определения радиуса дорожки качения наружного кольца
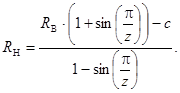 (3)
(3)
Формулу для прямого передаточного отношения планетарного механизма с ЗСТК с диаметрами равной величины и зазором при ведущем наружном кольце, неподвижном внутреннем кольце и сепараторе (водило) в качестве выходного звена получим, используя метод обращенного движения
![]() (4)
(4)
где ![]() – внутреннее передаточное отношение механизма рассматриваемого вида.
– внутреннее передаточное отношение механизма рассматриваемого вида.
Внутреннее передаточное отношение механизма с ЗСТК с диаметрами равной величины при тех же условиях представим в виде
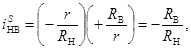 (5)
(5)
здесь знаки «-» и «+» соответствуют внутреннему и внешнему контактам дорожек качения наружного и внутреннего колец с телами качения.
Подставив (3) в (5) и преобразовав, будем иметь
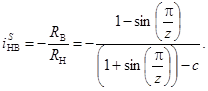 (6)
(6)
С учетом (6) приведем формулу (4) к окончательному виду
 (7)
(7)
Формула (7) позволяет определить прямое передаточное отношение планетарных механизмов с ЗСТК с диаметрами равной величины и зазором при ведущем наружном кольце, неподвижном внутреннем кольце и сепараторе (водило) в качестве выходного звена для обоих направлений ввода поправки в расчет геометрических параметров.
Обратное передаточное отношение механизмов рассматриваемого вида имеет место при ведущем сепараторе (водило), неподвижном внутреннем кольце и наружном кольце в качестве выходного звена, тогда с учетом (7) получим
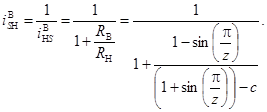 (8)
(8)
Варьируя числом тел качения в диапазоне (0-100) и значением радиуса дорожки качения наружного кольца в интервале (55-100) мм, проведем вычисления по выражениям (6)-(8) для всех видов передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины и зазором ![]() . Расчет выполняем по начальным условиям согласно системе (1). С целью повышения эффективности процесса вычислений авторами разработано программное обеспечение в виде программного комплекса «Эксцентрик» зарегистрированного в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности Российской Федерации (РОСПАТЕНТ № 2012614197).
. Расчет выполняем по начальным условиям согласно системе (1). С целью повышения эффективности процесса вычислений авторами разработано программное обеспечение в виде программного комплекса «Эксцентрик» зарегистрированного в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности Российской Федерации (РОСПАТЕНТ № 2012614197).
Анализ результатов вычислений показывает, что изменение радиуса дорожки качения наружного кольца в выбранном интервале не оказывает существенного влияния на диапазоны значений передаточных отношений механизмов рассматриваемого вида. По результатам полученных вычислений, выполняем синтез диаграммы передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины при ведущем наружном кольце и вводе поправки по радиусу дорожки качения этого же звена (рис. 2).
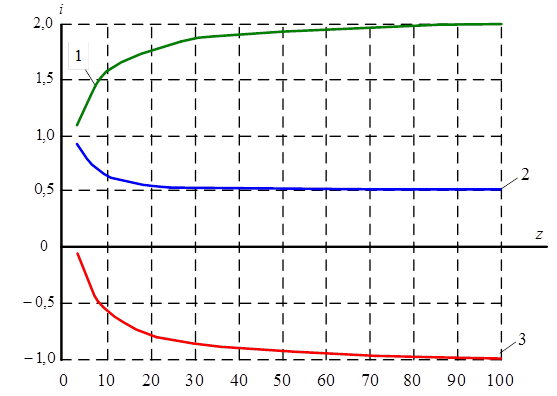
Рис. 2 Диаграмма передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины при ведущем наружном кольце и вводе поправки по
радиусу дорожки качения этого же звена: 1 – ![]() ; 2 –
; 2 – ![]() ; 3 –
; 3 – ![]()
Анализ диаграммы (рис. 2) показывает, что ввод поправки в расчет по радиусу дорожки качения наружного кольца позволяет планетарным механизмам с ЗСТК с диаметрами равной величины обладать передаточными отношениями в диапазонах: прямое ![]() , обратное
, обратное ![]() и внутреннее
и внутреннее ![]() . Это означает, что рассматриваемые механизмы являются редукторами, т. е. силовыми механизмами, так как прямое передаточное отношение
. Это означает, что рассматриваемые механизмы являются редукторами, т. е. силовыми механизмами, так как прямое передаточное отношение ![]() . Значения обратного передаточного отношения указывает на то, что при ведущем сепараторе (водило), неподвижном наружном кольце и внутреннем кольце в качестве выходного звена планетарные механизмы с ЗСТК при данных условиях находятся в режиме мультипликатора, так как
. Значения обратного передаточного отношения указывает на то, что при ведущем сепараторе (водило), неподвижном наружном кольце и внутреннем кольце в качестве выходного звена планетарные механизмы с ЗСТК при данных условиях находятся в режиме мультипликатора, так как ![]() , т. е. являются кинематическими механизмами. Ввод поправки по выбранному направлению обеспечивается максимально возможные величины передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины. При этом увеличение числа тел качения привод к росту только прямого передаточного отношения, так как при данных условиях внутреннее и обратное передаточные отношения уменьшаются.
, т. е. являются кинематическими механизмами. Ввод поправки по выбранному направлению обеспечивается максимально возможные величины передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины. При этом увеличение числа тел качения привод к росту только прямого передаточного отношения, так как при данных условиях внутреннее и обратное передаточные отношения уменьшаются.
Разработанный алгоритм определения передаточных отношений механизмов с ЗСТК с диаметрами равной величины применим для любого вида симметричной структурной схемы механизмов рассматриваемого вида при ведущем наружном кольце и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Полученные результаты прошли апробацию на международной научно-практической конференции (проект Sworld) [9, 10], а также на IV-ой международной научно-практической дистанционной конференции посвященной теме "Наука и образование" [11].
Заключение
В результате проведенных действий выявлены все виды передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины при ведущем наружном кольце, получены формулы для определения их величин, а также установлены возможные диапазоны их значений и режимы работы формируемых механизмов при вводе поправки в расчет по дорожке качения наружного кольца. Это позволяет формировать привода технологического оборудования на базе планетарных механизмов с ЗСТК обладающих требуемыми величинами передаточных отношений, а также посредством согласования выходных и входных параметров энергетической и рабочей машин обеспечить работоспособность привода технологического оборудования. Используя результаты исследования, авторами усовершенствованно программное обеспечение, которое представляет собой программный комплекс «Эксцентрик» зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ № 2012614197).
Рецензенты:
Меновщиков В.А., д.т.н., профессор, профессор кафедры «Прикладная механика», ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск;
Носков М.В., д.ф-м.н., профессор, профессор-наставник, руководитель НУЛ методики электронного обучения кафедры ПМиКБ, Институт космических и информационных технологий ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Библиографическая ссылка
Мерко М.А., Колотов А.В., Меснянкин М.В., Митяев А.Е., Кайзер Ю.Ф., Лысянников А.В., Лысянникова Н.Н., Кузнецов А.В., Литвинов П.С., Белякова С.А. ПЕРЕДАТОЧНЫЕ ОТНОШЕНИЯ ПЛАНЕТАРНЫХ МЕХАНИЗМОВ С ЗСТК С ДИАМЕТРАМИ РАВНОЙ ВЕЛИЧИНЫ ПРИ ВЕДУЩЕМ НАРУЖНОМ КОЛЬЦЕ И ВВОДЕ ПОПРАВКИ ПО РАДИУСУ ДОРОЖКИ КАЧЕНИЯ ЭТОГО ЖЕ ЗВЕНА // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17100 (дата обращения: 22.02.2026).



