Широкозонные полупроводниковые материалы на основе твердых растворов карбида кремния позволяют создавать приборы с повышенной стойкостью к различным внешним воздействиям (тепловому, механическому, химическому, радиационному).
Твердые растворы квазибинарной системы (SiC)1-x(AlN)x представляют значительный интерес для устройств экстремальной электроники благодаря тому, что их ширина запрещенной зоны изменяется от 2,9 эВ в чистом карбиде кремния до 6,2 эВ в чистом нитриде алюминия. В зависимости от состава твердого раствора (SiC)1-x(AlN)x могут быть созданы эффективные устройства как для силовой, так и оптоэлектроники. Для силовых приборов обеспечивается значительное снижение сопротивления в открытом состоянии и, следовательно, увеличение удельной мощности. Для оптоэлектронных приборов применение твердых растворов (SiC)1-x(AlN)x обеспечивает создание эффективных устройств светодиодов с широким спектром излучения, в том числе ультрафиолетовой области с длинной волны в максимуме спектра от 350 до, по крайней мере, до 240 нм.
Ранее считалось, что получить твердые растворы на основе нитридов III группы с различным составом компонент не позволяет, по существующим представлениям, наличие области несмешиваемости на диаграмме состояния. Рассчитанная Зангвилом (Zangvil) и Рухом (Ruh) фазовая диаграмма системы SiC-AlN показывает наличие твердого раствора выше температуры 2300 К и отсутствие растворимости ниже её [1].
Несмотря на предположение о тенденции к несмешиваемости при низких температурах синтеза, последние экспериментальные результаты показывают возможность получения пленок твердых растворов (SiC)1-х(AlN)x во всем диапазоне составов при х от 1 до 0 [2]. Получены обнадеживающие результаты по получению монокристаллических слоёв (SiC)0,7(AlN)0,3 на монокристаллической подложке карбида кремния при температуре в районе 1000 0С [3]. В последние годы появились теоретические и экспериментальные работы по возможности образования твердых растворов и при более низких температурах [4, 5].
В настоящей работе с позиции физико-химии и теории смешения рассматривается дополнительное обоснование возможности образования твердых растворов в системе SiC-AlN с использованием модели изоморфного замещения атомов в катионных и анионных подрешетках.
Экспериментальные результаты
Проведена серия экспериментов по получению пленок (SiC)1-х(AlN)x магнетронным распылением поликристаллической мишени твердого раствора (SiC)1-х(AlN)x с содержанием AlN при х = 0,3 и 0,5. Рентгеновская дифрактометрия показала, что материал мишени состоит из двух гексагональных фаз, отличающихся периодами решеток. Количественно фаза 2Н составляет 98%, 4Н - 2% (рисунок 1). Это может объясняться тем, что карбид кремния и нитрид алюминия имеют две разные решетки. После спекания основная часть SiC и AlN трансформировалась в фазу 2Н, а незначительная часть SiC осталась в фазе 4Н.
Подложками служили монокристаллические пластины кремния и карбида кремния. Осаждение плёнок осуществлялось с помощью магнетрона постоянного тока планетарного типа как без предварительного нагрева подложки, так и при различных температурах до 1300 0С. Рабочим газом служил аргон высокой чистоты. Плотность ионного тока изменялась в пределах 5-10 мА/см2 при энергии ионов 400-800 эВ.
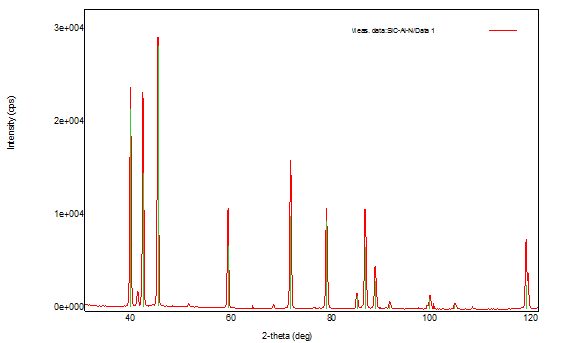
Рис.1. Рентгеновская дифрактограмма мишени (SiC)0,7(AlN)0,3
Анализ результатов по определению фазового и элементного состава полученных пленок методами рентгеновской дифрактометрии, вторичной ионной масс-спектрометрии и Оже-спектроскопии показал во всех случаях как наличие всех элементов твердого раствора, так и самого твердого раствора.
Данные исследования состава пленок (SiC)0,7(AlN)0,3, полученных при плотности ионного потока 8 мА/см2, по глубине образца представлены в таблице 1. Как и в случае с пленками (SiC)0,5(AlN)0,5, наблюдается равномерное распределение состава по толщине и достаточно низкое среднеквадратичное отклонение от состава мишени.
Результаты рентгеновского анализа слоев твердого раствора (SiC)0,7(AlN)0,3, полученных на подложках из 6Н-SiC магнетронным распылением при температуре 1000 0С, подтвердили возможность образования монокристаллической структуры твердого раствора (рисунок 2). Использованное отфильтрованное излучение CuKα, как правило, при достаточной разрешающей способности спектрографа регистрируется как дублет Kα1 и Kα2, что и наблюдается на рисунке. Кроме максимума от подложки на дифрактограмме наблюдается выраженный максимум, связанный с твердым раствором. Из-за близости величин постоянных решеток SiC и (SiC)0.7(AlN)0.3 максимумы дифракционных спектров на дифрактограмме отличаются незначительно. Отсутствие других рефлексов на дифрактограмме свидетельствует о монокристалличности полученных пленок.
Таблица 1
Послойный анализ состава образцов (SiC)0,7(AlN)0,3/Si
|
Элемент |
Послойный состав поверхности, ат. % |
|
|
5-30 нм |
50-70 нм |
|
|
Si |
34,7 |
36,1 |
|
C |
35,5 |
35,7 |
|
Al |
15,6 |
14,2 |
|
N |
14,2 |
14 |
|
Среднеквадратическое отклонение |
0,58 |
0,91 |
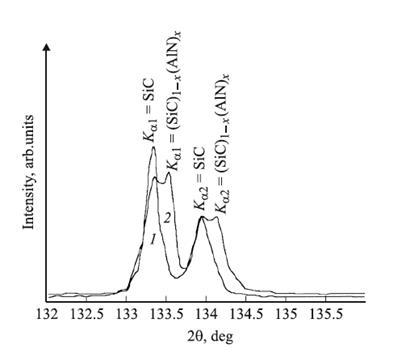
Рис. 2. Дифрактораммы подложки 6Н-SiC (1) и твердого раствора (SiC)0.7(AlN)0.3
Вся совокупность имеющихся экспериментальных результатов по получению твердых растворов в системе SiC-AlN, и, в частности, при магнетронном образовании плёнок, позволяет рассмотреть метод ионного замещения при образовании твердого раствора и уточнить фазовую диаграмму квазибинарной системы по результатам расчетов энергии образования твердого раствора.
Методика расчета межатомного взаимодействия в системе SiC-AlN
Предложенные Зангвилом и Рухом значения критической температуры для системы (SiC)1-х(AlN)x предполагают наличие возможности образования твердых растворов только при температурах выше 2300 К или же исключительно при малых концентрациях одной из компонент (при х→0 и х→1) (рисунок 3). Современные методы получения твердых растворов показали возможность образования таковых во всем диапазоне х и при гораздо более низких температурах. В связи с этим возникла необходимость согласования экспериментальных и теоретических данных.
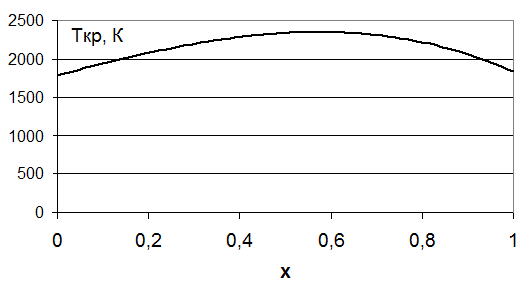
Рис. 3. Зависимость критической температуры от состава твердого раствора (SiC)1-х(AlN)x, рассчитанная Зангвилом и Рухом.
Для уточнения модели образования твердых растворов в системе (SiC)1-х(AlN)x были произведены расчеты, основанные на классической теории смешения [6] и методе Урусова-Хиенталы [7]. Данный метод позволяет получить дополнительное согласование экспериментальных и теоретических результатов по оценке термодинамической устойчивости и растворимости элементов I-VI групп в гексагональных нитридах алюминия, галлия, индия бора и других элементов [8].
Согласно уравнению Беккера может быть найдена критическая температура Ткр, ниже которой раствор распадается на две фазы [8]:
Ткр = 0,835 Ω / 2R, (1)
где R – газовая постоянная,
Ω – параметр взаимодействия.
Критическая температура является важным параметром при анализе возможности существования твердых растворов. Однако из-за малых значений коэффициента самодиффузии в полупроводниках при низких температурах выпадение второй фазы при охлаждении ниже критической температуры наблюдается редко.
Параметр взаимодействия Ω определяет термодинамическую устойчивость твердых растворов. В наиболее обобщенном виде параметр взаимодействия можно выразить как сумму деформационной Ωi, электростатической Ωe, структурной Ωs и вакансионной Ωv составляющих соответственно:
Ω = Ωi + Ωe + Ωs + Ωv (2)
Структурная составляющая параметра взаимодействия Ωs в выражении (4) равна энтальпии фазового перехода и учитывается, когда кристаллические решетки соединений отличаются. Считается, что в соединениях AIIIBV эта величина составляет ~5 ккал/моль. Ее влияние может сказываться только в системах с малой разностью параметров решеток. Вероятность образования растворов вычитания полагают малой из-за большой величины энергии образования вакансий в нитридах.
Деформационная составляющая может быть найдена как аддитивная величина:
Ωi = 9φ (1-3/v) V [x(∆r/r1)2 + (1-x) (∆r/r2)2] /2β, (3)
где v — координационное число;
V — удельный объем при формальном соблюдении правила Вегарда;
β — коэффициент сжимаемости;
ri — межатомное расстояние в i-й компоненте раствора;
φ – дополнительный коэффициент ассиметрии, вводимый в случае значительного отличия упругих свойств.
Сжимаемость определяется как величина, обратная модулю объемной упругости.
Электростатическая составляющая может быть найдена из соотношения:
Ωe = α Z+ Z- (∆fi)2 /(V)1/3 , (4)
где Z+ и Z- — формальная валентность атомов;
∆fi — разность долей ионности компонентов раствора;
α — константа Маделунга.
По формуле (2) был рассчитан параметр взаимодействия Ω для системы SiC-AlN, где существенный вклад имеют только деформационная и электростатическая составляющая. Значение параметра взаимодействия в зависимости от состава представлены в таблице 2. Результаты расчета критической температуры при данном параметре взаимодействия представлены на рисунке 4 (а). Расчет производился по классической модели, при которой учитывалась вероятность попадания катионов и анионов в противоположные решетки. При этом значения электростатической и деформационной составляющей существенно возрастали из-за значительной разницы в параметрах подрешетки.
Несмотря на то, что полученные по данной методике значения критической температуры ниже значений, предложенных Зангвилом и Рухом, рассогласование между теоретически рассчитанной температурой и экспериментальными данными довольно велико.
Табл. 2. Зависимость параметра взаимодействия Ω от состава твердого раствора (SiC)1-х(AlN)x, рассчитанная на основе классической теории смешения.
|
Состав твердого раствора (SiC)1-х(AlN)x, х |
00 |
00,1 |
00,2 |
00,3 |
00,4 |
00,5 |
00,6 |
00,7 |
00,8 |
00,9 |
11 |
|
Параметр взаимо-действия Ω, кДж/моль |
15,9 |
21,5 |
24,9 |
28,1 |
30,7 |
31,8 |
31 |
28,9 |
26,1 |
23,7 |
19,9 |
Было выдвинуто предположение, при смешении атомов в системе SiC-AlN происходит изоморфное ионное замещение. Т.е. замещение атомов кремния в подрешетке кремния возможно только на атомы алюминия и наоборот. Аналогично и для подрешеток углерода и азота. Таким образом, исходя из предположения, что в твердом растворе (SiC)1-х(AlN)x не происходит попадания анионов в катионную решетку и наоборот, по формуле (2) был рассчитан параметр взаимодействия с учетом модели изоморфного ионного замещения. В данном случае существенно снизилось значение как деформационной, так и электростатической составляющей. Значения параметра взаимодействия для системы (SiC)1-х(AlN)x в приближении модели изоморфного ионного замещения в зависимости от состава представлены в таблице 3. Рассчитанная на основе этих значений критическая температура показана на рисунке 4 (б).
Таб. 3. Зависимость параметра взаимодействия от состава твердого раствора (SiC)1-х(AlN)x, рассчитанная по модели изоморфного ионного замещения.
|
Состав твердого раствора (SiC)1-х(AlN)x, х |
00 |
00,1 |
00,2 |
00,3 |
00,4 |
00,5 |
00,6 |
00,7 |
00,8 |
00,9 |
11 |
|
Параметр взаимо-действия Ω, кДж/моль |
12,5 |
13,6 |
14,6 |
15,5 |
16,3 |
16,7 |
16,4 |
15,9 |
15,3 |
14,5 |
13,9 |
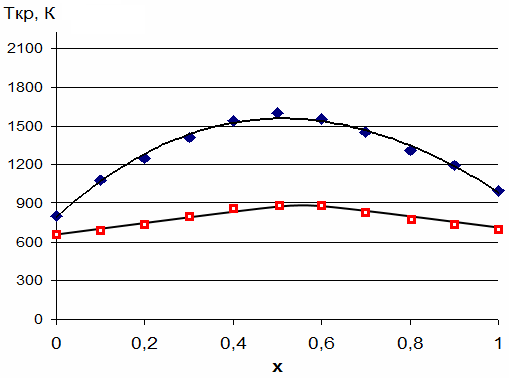
Рис. 4. Результаты расчета зависимости критической температуры от состава твердого раствора (SiC)1-х(AlN)x: а) на основе классической теории смешения (♦); б) по модели изоморфного ионного замещения (□);
Полученные с применением модели изоморфного ионного замещения значения параметра взаимодействия и критической температуры позволяют обосновать возможность экспериментального получения твердых растворов во всем диапазоне х и при температурах ниже 900 К. Данные результаты дополняют и удовлетворительно согласуются с данными по кластерному механизму формирования твердых растворов в системе SiC-AlN при пониженных температурах [9].
Заключение
Полученные экспериментальные результаты по получению пленок твердых растворов (SiC)1-х(AlN)x магнетронным распылением мишени показали возможность формирования слоев аналогичного элементного и фазового составов мишени при любой температуре подложки даже без предварительного её нагрева. Данное обстоятельство позволило рассмотреть и дополнить механизм образования твердого раствора при низких температурах. Существующие представления позволяли лишь предполагать образование твердых растворов при температурах более 1300 К. Полученные нами результаты позволили дополнить информацию о модели образования твердого раствора при низкой температуре. Модель изоморфного ионного замещения позволяет объяснить, почему на практике удается синтезировать пленки твердых растворов (SiC)1-х(AlN)x в диапазоне 0 < x < 1.
Рецензенты:
Мурашев В.Н., д.т.н., профессор кафедры Полупроводниковой электроники и физики полупроводников НИТУ «МИСиС», г. Москва;
Наими Е.К., д.ф.-м.н., профессор кафедры Физики НИТУ «МИСиС», г. Москва.
Библиографическая ссылка
Харламов Н.А., Кузнецов Г.Д., Евсеев В.А., Билалов Б.А., Каргин Н.И. К МОДЕЛИ ОБРАЗОВАНИЯ ТВЕРДЫХ РАСТВОРОВ В СИСТЕМЕ SIC-ALN ПРИ МАГНЕТРОННОМ НАНЕСЕНИИ ПЛЕНОК // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=17049 (дата обращения: 23.02.2026).



