Целью управления финансовыми активами является достижение определенного экономического эффекта в будущем. В частности, инвестор (держатель фондового портфеля) старается максимизировать доходность и минимизировать риск неэффективности своих инвестиций. Так как будущее состояние активов и их окружения неизвестно, то управление протекает в условиях неопределенности, которая порождает риск неэффективного управления.
Существуют классические подходы к составлению оптимальной структуры портфеля ценных бумаг (ПЦБ), в основе которых лежит рассмотрение доходности ценной бумаги (ЦБ) как статистического случайного процесса, однако используемые в них допущения не вполне согласованы с реальностью фондового рынка.
Основная проблема в том, что процессы, протекающие на фондовом рынке, часто неустойчивы и неоднородны. Неопределенность – неотъемлемое свойство рынка ценных бумаг. Таким образом, нельзя утверждать статистическую однородность случайного процесса доходности ЦБ при классическом понимании вероятности [3]. Вследствие этого вполне логичен вывод, что характер связи между доходами различных типов бумаг не может быть описан статистически.
Здесь следует заметить следующее. В классической модели составления ПЦБ для определения доходности акции используются значения ее цены, снятые единожды в каждый момент времени (например, один раз в течение торгового дня). При этом не учитывается тот факт, что на протяжении торгового дня стоимость акции колеблется в определенном интервале от минимального значения к максимальному. Чтобы учесть размытость исходных данных во времени, уместно использовать для описания доходности ЦБ треугольные нечеткие числа. Для этого нужно модифицировать известную модель построения оптимальной структуры ПЦБ [2] с использованием аппарата нечетких множеств.
Примем в рассмотрение то, что в течение торгового дня стоимость ЦБ изменяется непрерывно, достигая некоего максимального и минимального значения, и дадим определение доходности ценной бумаги как треугольного нечеткого числа.
Пусть для отрезка времени ![]() определены три параметра
определены три параметра ![]() -й бумаги: стоимость в момент открытия торгов (
-й бумаги: стоимость в момент открытия торгов (![]() ), а также максимальная (
), а также максимальная (![]() ) и минимальная (
) и минимальная (![]() ) стоимость,
) стоимость, ![]() ,
, ![]() , здесь
, здесь ![]() – число рассматриваемых видов ценных бумаг,
– число рассматриваемых видов ценных бумаг, ![]() – число наблюдений. Тогда максимальная доходность ЦБ
– число наблюдений. Тогда максимальная доходность ЦБ ![]() – отношение максимально возможной прибыли за выбранный период, полученной инвестором за время владения ценной бумагой, к затратам на её приобретение:
– отношение максимально возможной прибыли за выбранный период, полученной инвестором за время владения ценной бумагой, к затратам на её приобретение:
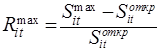 (1)
(1)
Аналогично, минимальная доходность ЦБ – отношение минимально возможной прибыли за выбранный период, полученной инвестором за время владения ценной бумагой, к затратам на её приобретение:
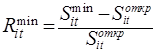 (2)
(2)
Исходя из этого, можно представить доходность ценной бумаги в момент времени ![]() в виде треугольного нечеткого числа:
в виде треугольного нечеткого числа:
![]() , (3)
, (3)
где![]() .
.
Функция принадлежности такого числа имеет треугольный вид (рис. 1).
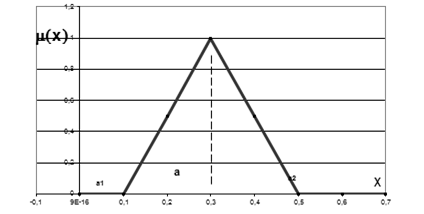
Рис. 1. Функция принадлежности треугольного нечеткого числа
В нечеткой арифметике операции над нечеткими числами вводятся через операции над функциями принадлежности. При этом используется понятие уровня принадлежности ![]() (
(![]() -уровня) как ординаты функции принадлежности нечеткого числа. Тогда пересечение функции принадлежности с нечетким числом дает пару значений, которые принято называть границами интервала достоверности. Основные операции с нечеткими числами сводятся к операциям с действительными числами – четкими значениями (степень принадлежности которых равна единице) и границами интервалов. Подробно с операциями над нечеткими числами можно ознакомиться в [4].
-уровня) как ординаты функции принадлежности нечеткого числа. Тогда пересечение функции принадлежности с нечетким числом дает пару значений, которые принято называть границами интервала достоверности. Основные операции с нечеткими числами сводятся к операциям с действительными числами – четкими значениями (степень принадлежности которых равна единице) и границами интервалов. Подробно с операциями над нечеткими числами можно ознакомиться в [4].
Если мы имеем дело с историей котировок ЦБ за некоторый временной промежуток, то, представляя ее доходность в виде (3) в каждый момент времени, получим нечетко-случайную величину доходности ЦБ. Для нечетко-случайных величин, как и для обычных случайных величин, определены понятия математического ожидания и дисперсии [5]. Так, ожидаемая доходность акции ![]() , учитывая правило сложения треугольных нечетких чисел, рассчитывается следующим образом:
, учитывая правило сложения треугольных нечетких чисел, рассчитывается следующим образом:
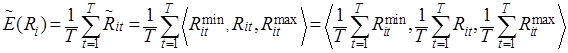 (4)
(4)
Введем обозначения:
![]()
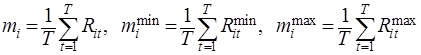
Тогда элемент матрицы к вариации ![]() доходностей акций также является нечетким числом и имеет вид:
доходностей акций также является нечетким числом и имеет вид:
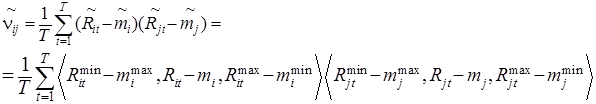 (5)
(5)
Будущая доходность портфеля ![]() представляется нечеткой функцией, поскольку нечеткими являются значения доходностей ЦБ, входящих в него:
представляется нечеткой функцией, поскольку нечеткими являются значения доходностей ЦБ, входящих в него:
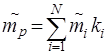 (6)
(6)
Риск портфеля ![]() также является нечеткой функцией вида
также является нечеткой функцией вида
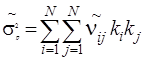 (7)
(7)
Для нахождения оптимальной структуры портфеля будем максимизировать функцию
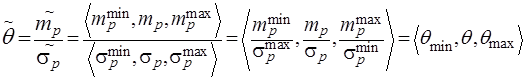 , (8)
, (8)
при условии
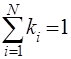 , (9)
, (9)
где ![]() – доля портфеля, инвестированная в ЦБ типа
– доля портфеля, инвестированная в ЦБ типа ![]() .
.
Функция ![]() является нечеткой функцией четкого аргумента, поскольку инвестор желает совершенно точно знать, в каком количестве ему следует приобретать ЦБ каждого вида, чтобы составить свой фондовый портфель. Заметим, что дифференцирование треугольной нечеткой функции проводится по правилам вещественного дифференцирования [1].
является нечеткой функцией четкого аргумента, поскольку инвестор желает совершенно точно знать, в каком количестве ему следует приобретать ЦБ каждого вида, чтобы составить свой фондовый портфель. Заметим, что дифференцирование треугольной нечеткой функции проводится по правилам вещественного дифференцирования [1].
Наша нечеткая функция задана в виде ![]() . В таком случае дифференцирование по аргументам
. В таком случае дифференцирование по аргументам ![]() будем производить следующим образом:
будем производить следующим образом:
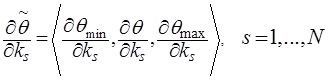 (10)
(10)
С помощью дифференцирования и преобразований, аналогичных проведенным в [2], получим системы ![]() линейных неоднородных уравнений с нечеткими коэффициентами для среднего, левого граничного и правого значения функции
линейных неоднородных уравнений с нечеткими коэффициентами для среднего, левого граничного и правого значения функции ![]() . Также воспользуемся понятием
. Также воспользуемся понятием ![]() -уровня нечеткого числа, т.е. представим
-уровня нечеткого числа, т.е. представим
![]() ;
;![]() ;
;
![]() .
.
С учетом такого представления системы принимают вид:
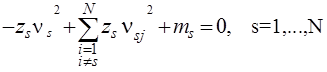 (11)
(11)
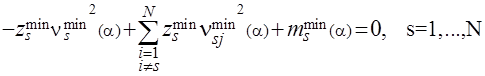 (12)
(12)
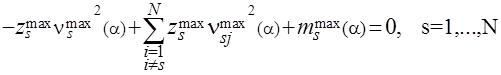 (13)
(13)
Для каждого конкретного ![]() -уровня эти три системы содержат только четкие числа и могут быть решены относительно
-уровня эти три системы содержат только четкие числа и могут быть решены относительно ![]() ,
, ![]() и
и ![]() . Затем для каждой системы могут быть найдены доли
. Затем для каждой системы могут быть найдены доли ![]() ,
, ![]() ,
, ![]() ценных бумаг, из которых составляется портфель:
ценных бумаг, из которых составляется портфель:
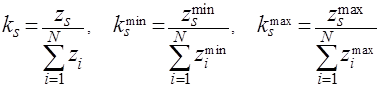 (14)
(14)
Нижняя граница ![]() -уровня, то есть его минимальное рассматриваемое значение, задается экспертом самостоятельно. В нашей работе мы приняли
-уровня, то есть его минимальное рассматриваемое значение, задается экспертом самостоятельно. В нашей работе мы приняли ![]() .
.
Для демонстрации описанной модели составим ПЦБ из нескольких видов ценных бумаг, определим его оптимальную структуру и сравним его характеристики (доходность, риск, критерий эффективности, равный отношению доходности к риску) с портфелем, составленным по известной вероятностной модели [2].
Для построения портфеля ценных бумаг по предложенной модели были взяты данные за апрель – май 2014 г. о ценных бумагах семи из пятидесяти предприятий, на основании стоимости которых строится индекс РТС. Были рассмотрены четыре суточных показателя: стоимость бумаги в момент открытия торгов, в середине торгового дня, а также максимальная и минимальная ее стоимость в течение торгового дня.
С данными о стоимостях акций этих предприятий можно ознакомиться на сайте электронного ресурса [6], в разделе «РТС». На основе этих данных по формуле (4) были рассчитаны доходности ценных бумаг (таблица 1). В столбце ![]() содержатся значения доходностей, вычисленные по [2] с использованием единственного измерения стоимости цены акций в середине торгового дня.
содержатся значения доходностей, вычисленные по [2] с использованием единственного измерения стоимости цены акций в середине торгового дня.
Таблица 1. Доходности ЦБ
|
Предприятие |
|
|
|
|
|
ОАО Сбербанк России |
0,001201 |
-0,013438 |
0,015840 |
0,000907 |
|
ОАО Мобильные ТелеСистемы |
0,004038 |
-0,008393 |
0,016468 |
0,002579 |
|
ОАО Мегафон |
0,001779 |
-0,007704 |
0,011262 |
0,001242 |
|
ОАО Магнит |
0,000554 |
-0,014184 |
0,015292 |
0,002529 |
|
ОАО Северсталь |
0,003785 |
-0,014539 |
0,022110 |
0,001204 |
|
ОАО Газпром |
0,002982 |
-0,006314 |
0,012278 |
0,002116 |
|
ОАО АК Транснефть |
0,002474 |
-0,007497 |
0,012446 |
0,001828 |
С помощью представленного выше алгоритма были найдены доли ЦБ ![]() ,
, ![]() ,
, ![]() для всех
для всех ![]() . Затем, по формуле (8), для каждого
. Затем, по формуле (8), для каждого ![]() были определены значения
были определены значения ![]() и
и ![]() . Наконец, на базе этих значений была построена функция принадлежности
. Наконец, на базе этих значений была построена функция принадлежности ![]() (рис. 2).
(рис. 2).
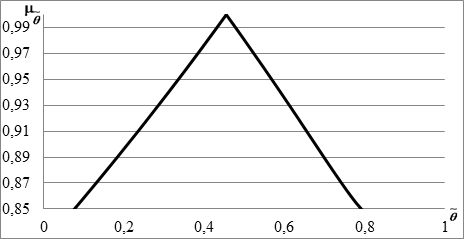
Рис. 2. Функция принадлежности критерия эффективности портфеля
Максимум функции принадлежности ![]() соответствует наиболее достоверному значению
соответствует наиболее достоверному значению ![]() . Оно является вещественным числом, т.е. можно однозначно определить структуру ПЦБ, соответствующую такому
. Оно является вещественным числом, т.е. можно однозначно определить структуру ПЦБ, соответствующую такому ![]() , причем она будет оптимальной. Доли ЦБ в итоговом портфеле, соответствующем максимальному критерию эффективности по предложенной нечеткой модели, распределились следующим образом (таблица 2). Также таблица содержит доли ЦБ в портфеле, структура которого рассчитана по известной вероятностной модели.
, причем она будет оптимальной. Доли ЦБ в итоговом портфеле, соответствующем максимальному критерию эффективности по предложенной нечеткой модели, распределились следующим образом (таблица 2). Также таблица содержит доли ЦБ в портфеле, структура которого рассчитана по известной вероятностной модели.
Таблица 2. Доли ЦБ в итоговом портфеле
|
Предприятие |
Доля ЦБ в портфеле |
|
|
Нечеткая модель |
Вероятностная модель |
|
|
ОАО Сбербанк России |
0,1560 |
0,1261 |
|
ОАО Мобильные ТелеСистемы |
0,1337 |
0,2652 |
|
ОАО Мегафон |
0,2910 |
0,1738 |
|
ОАО Магнит |
0,1319 |
0,1377 |
|
ОАО Северсталь |
0,0772 |
0,0597 |
|
ОАО Газпром |
0,0600 |
0,1202 |
|
ОАО АК Транснефть |
0,1502 |
0,1173 |
Главные характеристики портфелей, полученных по обеим моделям, приведены в таблице 3.
Таблица 3. Характеристики портфелей
|
Характеристика |
Значение |
|
|
Нечеткая модель |
Вероятностнаямодель |
|
|
Доходность |
0,00216 |
0,00190 |
|
Риск |
0,004752 |
0,005471 |
|
Критерий эффективности |
0,45477 |
0,34784 |
Из таблицы видно, что ПЦБ, составленный в соответствии с предложенной в данной работе моделью, имеет большую доходность и меньший риск, в сравнении с тем, который составлен по известной вероятностной модели. Таким образом, модель с использованием нечетких чисел дает более эффективный портфель, чем известная модель, с точки зрения выбранного критерия (отношение доходности портфеля к его риску). Это обуславливается тем, что в рассмотрение принято не одно конкретное значение стоимости ценной бумаги из какого-то временного интервала, а описание изменения стоимости за некоторый промежуток времени в виде треугольного нечеткого числа. Таким образом, на основании данной работы можно с определенной степенью уверенности утверждать, что применение теории нечетких чисел позволяет получить более эффективные результаты при оптимизации ПЦБ по сравнению с результатами, установленными на основе других известных методик.
Рецензенты:
Роговой А.А., д.ф.-м.н., профессор, научный сотрудник Института механики сплошных сред, г. Пермь;
Перский Ю.К., д.э.н., профессор Пермского национального исследовательского политехнического университета, г. Пермь.
Библиографическая ссылка
Севодин М.А., Козловская Я.И. ОБ ИСПОЛЬЗОВАНИИ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ ПРИ ПОСТРОЕНИИ ОПТИМАЛЬНОЙ СТРУКТУРЫ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16913 (дата обращения: 23.02.2026).



