Прогнозирование ледового сопротивления предусматривает использование аналитических или экспериментальных методов. Несмотря на значительный прогресс в развитии расчетных методов, экспериментальные исследования ледовой ходкости судов являются наиболее надежными. Эти испытания проводятся в ледовых бассейнах, число которых непрерывно растет. Лабораторные условия позволяют проводить в относительно короткие сроки модельные ледовые испытания в широком диапазоне изменения формы и размеров проектируемых судов и плавучих сооружений и в не меньшем диапазоне разнообразных ледовых условий. Таким образом, модельные испытания в ледовом бассейне являются универсальным способом оценки ледовых качеств судов и плавучих сооружений в различных ледовых условиях.
Существенная особенность льда как материала заключается в том, что в реальных условиях он находится при высокой гомологической температуре и процессы его деформирования часто сопровождаются фазовыми переходами, что требует особой тщательности в проведении исследований и их толковании.
В статье рассматривается новый подход к модельным исследованиям движения судна во льдах. Теоретические основы моделирования движения судна во льдах были разработаны Л.М. Ногидом [7] и Ю.А. Шиманским [9]. Из них вытекают требования к материалу модели льда (1) и критериям моделирования Фруда, Рейнольдса и Коши (2):
; 
; 
; 
;
; 
; ; 
, (1)
; 
; 
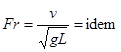где ρл, ρв – плотность льда и воды; Е, μ – модуль упругости и коэффициент Пуассона для льда и воды; σр – предел прочности льда на изгиб; f – коэффициент трения льда о корпус судна; v – скорость движения судна; 
– скорость движения судна; λ – геометрический масштаб, «н», «м» - индексы соотнесения с натурой и моделью.
Кроме того, как показали наши исследования, модель ледяного покрова должна иметь подобные диаграммы деформирования.
Трудности выполнения условий (1) общеизвестны, особенно в отношении упругих и прочностных характеристик (Е, σ), поэтому модель льда, полностью отвечающая этим условиям, пока не создана. Сложность также заключается и в том, что при разрушении льда значительных толщин, которое, как и для малых, происходит от изгиба, необходимо учитывать влияние смятия и среза в местах контакта с корпусом.
Пересчет ледового сопротивления, основанный на классической теории, приводит к существенному масштабному эффекту. Для его уменьшения разработано значительное количество искусственных приемов. В одних соотношение между Е и σ определяется эмпирически путем согласования результатов испытаний эталонной модели с экстраполяцией на другое судно, в других разными путями подбирается новая модель льда, более полно отвечающая условиям подобия, в третьих, в условиях разделения сопротивления на составляющие, используются эмпирические модели пересчета. В целом можно признать, что пока полностью адекватная модель льда для испытаний и пересчета результатов не создана.
Представляется закономерным представление полного сопротивления судна при движении во льдах по формуле[2, 4, 5, 7, 8, 9]
, (3)
где 
- сопротивление от разрушения сплошного ледяного покрова и трения корпуса о кромку неразрушенного льда; 
- сопротивление от взаимодействия корпуса с обломками льда (от притапливания, поворота, раздвигания обломков о корпус судна) и от трения обломков о корпус; 
- сопротивление воды.
Предполагаемый способ основан на раздельном моделировании составляющих и их пересчете на натуру.
Для модельных исследований разрушения льда необходимо смоделировать пространственную геометрию взаимодействия ледокола с ледяным покровом с образованием мест контакта корпуса с ледяным полем.
Подобие картин разрушения определяется подобием напряженно-деформированного состояния ледяной пластины, которое можно описать в аналитической постановке уравнением
, (4)
где w – прогиб льда; 
- оператор Лапласа; h – толщина льда; Е, μ – модуль упругости и коэффициент Пуассона для льда и воды;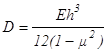 
- цилиндрическая жесткость ледяной пластины. Действующие на кромку льда усилия от давления корпуса определяются граничными условиями. Уравнение (4) в безразмерном виде записывается в виде
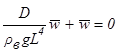, (5)
где 
– безразмерный прогиб. Подобие напряженно-деформированного состояния модели и натуры и геометрии образования трещин будет определяться условием
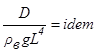(6)
Подставляя выражение для цилиндрической жесткости и полагая gн=gм, μн=μм, получим:
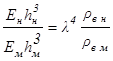(7)
В этом случае модуль пересчета толщин льда примет вид:
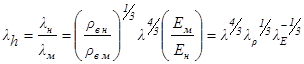, (8)
где 
, 
.
Если испытания модели проводятся в пресной воде, пересчет на натуру ведется для этих же условий 
. При пересчете на морскую воду при ρн≈1,025 т/м3, 
его можно также принять равным 1,0. Для реальной морской и пресной воды 
можно принять равной 1,0 и тогда
(9)
Определение модуля пересчета 
достаточно сложно, учитывая разнообразие методов определения Е, результаты которых отличаются в разы, и их слабую ориентированность при оценке толщины льда на их величину. Поэтому для ориентировочных определений воспользуемся следующими положениями:
- представляется реальная зависимость напряжений предела прочности льда на изгиб от толщины льда, полученная В.В. Лавровым [6] при отрицательных температурах и приведенная на рис.1. Приведенная зависимость с достаточной точностью аппроксимируется зависимостью
, (10)
где σр – предел прочности льда на изгиб, Мпа; h – толщина льда, м.
- с другой стороны известны результаты опытов на малых образцах (толщиной до 2,0 см и длиной 24 см) полученных Табатой [10] и приведенных на рис.1а.
(а)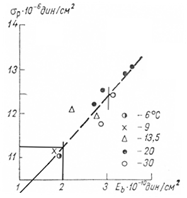
(б)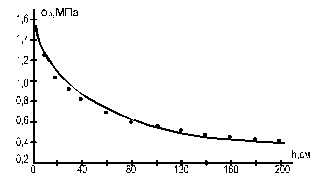 
Рис. 1. а) Зависимость между разрушающим напряжением и модулем деформации для разных температур [10] (обозначения сохранены по оригиналу) б) Зависимость σр от h по В.В. Лаврову [6]
Из опытов следует, что модуль деформации и изгибные напряжения зависят линейно, то есть 
(где k – коэффициент пропорциональности). В этом случае можно записать:
(11)
При оценке сопротивления разрушения льда в качестве модели льда предлагается использовать естественный лед, намороженный в бассейне при отрицательной температуре воздуха. На возможность такого подхода указывал еще Л.М. Ногид [7].
Естественный лед имеет повышенную прочность по сравнению со строгой теорией моделирования, поэтому, по-видимому, получило распространенное мнение о невозможности его использования. Однако при использовании естественного льда компенсировать повышенную прочность при изгибе можно меньшей толщиной, чем требуется (моделируется разрушение ледяного покрова).
Приведенные выше зависимости использовались для прогнозирования составляющей разрушения льда при движении судна. Для определения сопротивления от разрушения ледяного покрова воспользуемся наиболее полной характеристикой взаимодействия судна со льдом – работой по ломке льда [4,5]
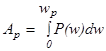(12)
где Р(w) – вертикальная сила, приложенная к ледяной пластине,
w – прогиб, при котором происходит полное разрушение льда.
Известны функциональные зависимости P(h) [2,4,5,8], представленные в виде
(13)
где k – коэффициент пропорциональности, зависящий от вида нагружения.
Для прогиба под вертикальной силой можно записать [4,5,10]
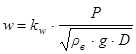(14)
где kw – коэффициент, зависящий от формы пластин в плане.
Формулы (12), (13), (14) позволяют получить масштабы пересчета сил, прогибов и работы
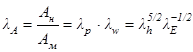(15)
Масштабы подобия по силе разрушения льда
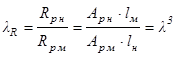(16)
Как показали наши эксперименты при пересчете толщин модели льда на натуру 
можно пренебречь влиянием 
. Формула (16) не противоречит строгой теории моделирования и ее можно использовать в новой модели льда.
При движении модели льда в сплошном ледяном поле кроме сопротивления разрушения сохраняется сопротивление обломков и сопротивление воды. Толщины обломков льда не соответствуют масштабу пересчета толщин - 
, поэтому их совместное моделирование с разрушением льда невозможно.
Наибольшее несоответствие возникает из-за сил плавучести и трения обломков, линейно зависящих от толщины льда. Инерционные составляющие, связанные с поворотом и раздвиганием льдин, а так же с присоединенными массами воды, меньше зависят от толщины, а больше от площади льдин. Поэтому для более строгого моделирования Rp и Rобл используется способ экспериментального разделения составляющих, требующих дополнительных испытаний в битом льду. Кстати, эти испытания могут быть и самостоятельными при определении сопротивления при движении в битых льдах
Разделение полного сопротивление на составляющие и их раздельное моделирование используется и в гипотезе Фруда при испытаниях моделей судов в воде.
Большое разнообразие ледовых условий, нестабильность характеристик битых льдов делают достаточно сложной точную фиксацию многочисленных параметров, характеризующих натурную ледовую обстановку (в том числе форму и размеры отдельных льдин, их сплоченность). Поэтому в эксперименте приближенно моделируется движение судна в некоторой условной среде с осредненными характеристиками. Условия подобия соблюдаются лишь в отношении наиболее важных характеристик битого льда (толщины, сплоченности, ширине канала, коэффициента трения льда о корпус).
Это дает возможность моделировать битый лед с помощью пластинок из полиэтилена высокого давления одинаковой формы и размеров и обеспечивает повторяемость опытов. Эти опыты можно проводить в обычном (не ледовом) бассейне.
У полиэтилена высокого давления ρл=0,92т/м3, f=0.15, что соответствует условиям подобия [7].
Для проведения таких испытаний необходимо выделить составляющую разрушения льда
(17)
Сопротивление обломков и воды определяется дополнительными испытаниями после прогонки модели в сплошном льду:
(18)
Сопротивление от разрушения льда пересчитывается на натуру следующим образом:
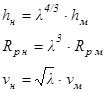(19)
Сопротивление модели в обломках определяется при испытаниях в плитках полиэтилена, толщина которых соответствует линейному масштабу модели. Сплоченность битого льда задается при испытаниях. Пересчет результатов соответствует теории моделирования. Пересчет на натуру производится по зависимостям:
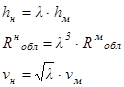(20)
При необходимости можно из сопротивления обломков выделить сопротивление воды при проведении дополнительных испытаний в чистой воде и определить сопротивление воды натуры общепринятым способом. Однако, учитывая малую долю сопротивления воды в общем балансе сил сопротивления, этого можно не делать, учитывая ее в сопротивлении вместе с обломками.
Формула (20) справедлива, если испытания проводятся в пресной воде и пересчет ведется на пресную воду. При пересчете на морскую воду необходимо вводить коэффициент, учитывающий изменение сил плавучести и трения из-за изменения плотности воды и льда. Этот коэффициент имеет вид:
(21)
На рис. 2 показаны фрагменты испытаний модели ледокола проекта 1105 в сплошном и в битом льду. В качестве примера на рис. 3 приведены результаты пересчета и диаграмма ледопроходимости речного ледокола проекта Р-47.
(а) 
(б) 
Рис. 2. Фрагменты испытаний модели ледокола проекта 1105 а) в естественном сплошном льду б) в битом льду (треугольные плитки полиэтилена)
(а) 
(б)
Рис. 3. a) Фрагмент испытаний модели ледокола R-50 в естественном льду
б) диаграмма ледопроходимости проекта Р-47 (*-пересчет на натуру; 1- данные натурных испытаний ЛИИВТа; 2 - данные натурных испытаний ГИИВТа)
Рецензенты:
Химич В.Л., д.т.н, профессор, заведующий кафедрой «Энергетические установки и тепловые двигатели» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Ваганов А.Б., д.т.н, доцент, заместитель заведующего кафедрой «Аэро-гидродинамика, прочность машин и сопротивление материалов» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Библиографическая ссылка
Семенов Д.А., Зуев В.А., Грамузов Е.М. НОВЫЕ ПОДХОДЫ К ЭКСПЕРИМЕНТАЛЬНЫМ ИССЛЕДОВАНИЯМ ЛЕДОВОГО СОПРОТИВЛЕНИЯ СУДОВ НА ИХ МОДЕЛЯХ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16869 (дата обращения: 20.04.2024).