В соответствии с действующими нормами (СП 63.13330.2012 «СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения») одним из обязательных этапов проектирования изгибаемых железобетонных конструкций является расчет по образованию нормальных трещин, который рекомендуется выполнять по предельным усилиям или по нелинейной деформационной модели. Проведенные в последние годы исследования [3, 5, 9] показывают, что предпочтение следует отдавать деформационной расчетной модели, хорошо отражающей фактический характер работы железобетона на всех этапах вплоть до его разрушения. Это позволяет с единых позиций выполнять расчеты железобетонных конструкций по прочности, трещиностойкости и по деформациям.
В частности, для определения усилия трещинообразования в нормальном сечении изгибаемого железобетонного элемента необходимо знать параметры диаграмм механического состояния бетона [2, 3, 8] и арматуры [4].При этом основные прочностные и деформативные характеристики материалов при сжатии и растяжении получают на стандартных образцах сравнительно небольших размеров, испытываемых при равномерном (однородном) распределении деформаций и напряжений в их поперечном сечении. Полученная в процессе таких испытаний равновесная диаграмма арматуры практически полностью соответствует условиям её работы в сечении железобетонного элемента [4]. Что касается диаграмм сжатия и растяжения бетона, то в изгибаемых железобетонных конструкциях условия работы бетона в сжатой и растянутой зонах существенно отличаются от соответствующих условий испытаний стандартных образцов, так как бетон работает в условиях неравномерного распределения деформаций и напряжений, т.е. при неоднородном деформировании [3, 8]. В первую очередь эта неравномерность отражается в существенном увеличении (в среднем в 1,75 раза) предельных величин относительных деформаций εbu и εbtu. Ранее в статье [7] на основе энергетического подхода автором представлена методика определения величин предельных относительных деформаций бетона εbu применительно к сжатой зоне изгибаемых железобетонных элементов при исчерпании прочности по нормальному сечению.
Представляется, что для начального этапа трещинообразования изгибаемого железобетонного элемента необходимотакже применить энергетический подход[1, 8], позволяющий из эталонной диаграммы центрального растяжения бетона получить её трансформированный аналог (рис. 1), который и определяет вид эпюры напряжений в растянутой зоне нормального сечения.
При этом обе диаграммы растяжения бетона в виде криволинейных зависимостей приняты без ниспадающей ветви, что объясняется невозможностью снижения величин нагрузок гравитационного характера, действующих на изгибаемые железобетонные конструкции.
В качестве эталонной диаграммы при осевом растяжении принимаем нелинейную кривую с начальным модулем упругости Ebt1, проходящую через предельную точку с координатами Rbt и ebtR (см. кривую 1 на рис. 1).
Для аналитического описания диаграммы растяжения бетона при центральном нагружении используем дробно-рациональную функцию вида [8]:
![]() , (1)
, (1)
где Ebt1, Dbt1,Cbt1 – начальный модуль упругости и параметры нелинейности деформирования бетона, получаемые экспериментально-теоретическим путем; sbt, ebt – текущие значения напряжений и деформаций при растяжении.
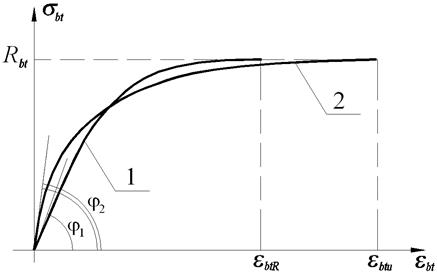
Рис. 1. Диаграммы деформирования бетона при центральном и неоднородном растяжении (кривые 1 и 2)): φ1 = arctg(Ebt1); φ2 = arctg(Ebt2)
Для нахождения указанных параметров диаграмм центрального растяжения бетона используются как экспериментальные (нормированные) данные [СП 63.13330.2012], так и общепринятые теоретические предпосылки[2, 3, 5].
К нормируемым параметрам относятся:
– предельное сопротивление бетона центральному растяжению Rbt;
– предельная относительная деформация бетона при центральном растяжении ebtR;
– нормативный модуль упругости бетона Ebn, величина которого должна устанавливаться при напряжении σb = 0,3Rb.
На основании обобщения данных, представленных в работах [2, 3, 6, 9], для определения величины ebtR применительно к тяжелому бетону классов от B10 до B100 можно рекомендовать следующую эмпирическую зависимость:
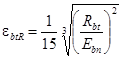 . (2)
. (2)
Что касается двух других параметров (Rbt, Ebn) то нормативная база их значений для широкого диапазона используемых в настоящее время бетонов достаточно хорошо разработана и постоянно пополняется.
Входящий в формулу (1) начальный модуль упругости Ebt1 отличается от нормативного модуля Ebn, который по существу является секущим модулем деформаций бетона при сжатии. Кроме того, согласно экспериментальным данным [6]начальные модули упругости бетона при сжатии и растяжении не равны между собой (Eb1 ≠ Ebt1). В этой же работе приводится эмпирическая зависимость, показывающая соотношение между этими величинами:
![]() , (3)
, (3)
где Eb1 – начальный модуль упругости бетона при сжатии, МПа, определяемый по формулам из работы [7]:
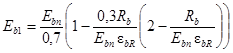 , (4)
, (4)
![]() . (5)
. (5)
Параметры нелинейности Dbt1, Cbt1 для уравнения (1), принятого для описания диаграммы центрального растяжения бетона, определяются исходя из следующих двух условий:
– конечная точка диаграммы центрального растяжения бетона имеет координаты sbt = Rbtи ebt = ebtR;
– касательный модуль деформаций в предельной точке диаграммы центрального растяжения равен нулю ![]() .
.
Указанные условия после соответствующих преобразований представлены следующими зависимостями:
![]() , (6)
, (6)
![]() . (7)
. (7)
Диаграмму деформирования бетона при неоднородном растяжении (см. кривую 2 на рис. 1) получаем путем трансформирования исходной (эталонной) диаграммы на основе использования энергетических соотношений[1, 8]. Для аналитического описания искомой диаграммы принимается функция, аналогичная (1) с учетом замены индексов при неизвестных параметрах (вместо 1 подставляется индекс 2).Для определения этих параметров (Ebt2, Dbt2,Cbt2) и искомой величины предельной относительной деформации (ebtu) приняты следующие гипотезы и допущения:
– предельное значение удельной энергии деформирования бетона при неоднородном растяжении(что соответствует растянутой зоне сечения изгибаемого элемента на этапе образования первой трещины) равно удельной энергии разрушения центрально растянутого бетонного образца;
– для предельной стадии деформирования бетона при неоднородном растяжении деформация волокна, проходящего через центр тяжести эпюры растягивающих напряжений, равна предельной деформации бетона при центральном растяжении ebtR;
– критерием начала процесса трещинообразования в нормальном сечении изгибаемого железобетонного элемента является достижение фибровым волокном растянутой зоны этого элемента предельной величины относительной деформации ebtu с одновременным исчерпанием сопротивления бетона растяжению Rbt;
– диаграмма неоднородного растяжения бетона имеет экстремум в точке с координатами sbt = Rbt и ebt = ebtu.
Аналитическое отображение принятых гипотез приводит к следующей системе уравнений:
![]() , (8)
, (8)
![]() . (9)
. (9)
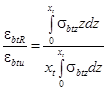 , (10)
, (10)
![]() , (11)
, (11)
где Dbt2,Cbt2 – параметры нелинейности диаграммы неоднородного растяжения бетона; xt – высота растянутой зоны бетона в сечении изгибаемого железобетонного элемента; z – текущее расстояние от нейтральной оси сечения до рассматриваемого волокна эпюры напряжений в растянутой зоне бетона; σbtz – текущее напряжение в рассматриваемом волокне эпюры напряжений; εbtz – текущая относительная деформация в рассматриваемом волокне эпюры деформаций в растянутой зоне бетона.
Зависимости (10) и (11) после интегрирования применительно к прямоугольному сечению изгибаемого железобетонного элемента будут иметь следующий вид:
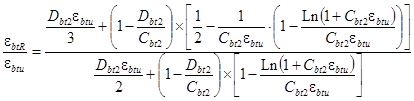 , (12)
, (12)
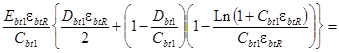
![]()
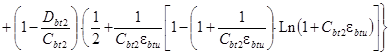 . (13)
. (13)
Пояснения к этим формулам были даны выше. Учитывая, что все полученные уравнения имеют нелинейный характер, то для их совместного решения применяется стандартная итерационная процедура, которая позволяет найти искомые характеристики диаграммы неоднородного растяжения бетона (Ebt2,Cbt2,Dbt2,ebtu).
Для получения количественных значений указанных параметров применительно к тяжёлому бетону были разработаны общий алгоритм и программа расчета "BETON_T", написанная для персонального компьютера на языке программирования «Pascal». Некоторые результаты расчетов, выполненных с помощью этой программы, представлены в следующей таблице 1.
Таблица 1
Параметры эталонной и трансформированной диаграмм растяжения тяжёлого бетона при кратковременном нагружении
|
Пара-метры |
Класс бетона |
|||||
|
B10 |
B20 |
B40 |
B60 |
B80 |
B100 |
|
|
Rbt, МПа |
0,85 |
1,35 |
2,10 |
2,75 |
3,30 |
3,80 |
|
Ebn, МПа |
19000 |
27500 |
36000 |
39500 |
42000 |
43000 |
|
Ebt1, МПа |
15360 |
23170 |
32810 |
38630 |
44000 |
48000 |
|
Cbt1 |
-5733,95 |
-5211,02 |
-4323,34 |
-3679,01 |
-3020,24 |
-2489,14 |
|
Dbt1 |
-7839,70 |
-7292,30 |
-6366,31 |
-5592,33 |
-5014,48 |
-4525,14 |
|
ebtR |
0,0000840 |
0,0000894 |
0,0001002 |
0,0001128 |
0,0001223 |
0,0001322 |
|
Ebt2, МПа |
38269 |
57827 |
82114 |
96847 |
110689 |
121068 |
|
Cbt2 |
31439,62 |
30077,55 |
27748,85 |
25135,69 |
24261,35 |
23293,90 |
|
Dbt2 |
-1024,47 |
-949,82 |
-824,07 |
-721,47 |
-641,96 |
-575,78 |
|
ebtu |
0,0001472 |
0,0001568 |
0,0001762 |
0,0001984 |
0,0002155 |
0,0002335 |
В частности, величины предельных относительных деформаций при осевом растяжении ebtR, найденные по предложенной формуле (2), возрастают от 0,000084 для бетона класса B10 до 0,0001322 для бетона B100. То есть принятое в СП 63.13330.2012 постоянное значение ebtR = 0,0001 примерно соответствует классу бетона В40, а для максимальной нормируемой прочности бетона (B100) этот параметр увеличивается на 32,2 %. Значения предельных относительных деформаций бетона при неоднородном растяжении ebtu также возрастают с ростом прочности бетона и укладываются в диапазон от 0,0001472 до 0,0002335.Отношение анализируемых параметров (ebtu / ebtR) не является постоянной величиной, которая увеличивается от 1,752 для бетона класса B10 до 1,766 для B100. Таким образом, согласно приведенным в таблице 1 данным, нормируемая предельная относительная деформация бетона при растяжении ebtu = 0,00015 в наибольшей степени соответствует только одному классу бетона (B20).
В заключение уместно отметить, что поскольку представленная методика определения величин предельных относительных деформаций бетона в растянутой зоне изгибаемых железобетонных элементов построена без привлечения эмпирических зависимостей, то можно говорить о возможности её применения для любых классов и видов конструкционных бетонов.
Рецензенты:
Меркулов С.И., д.т.н., проф., зав. кафедрой промышленного и гражданского строительства, ФГБОУВПО«Курский государственный университет», г. Курск;
Лесовик Р.В., д.т.н., проф., проректор по международной деятельности, профессор кафедры строительного материаловедения, изделий и конструкций, ФГБОУВПО «Белгородский государственный технологический университет им. В.Г. Шухова», г. Белгород.
Библиографическая ссылка
Никулин А.И. К ОПРЕДЕЛЕНИЮ ПРЕДЕЛЬНОЙ ОТНОСИТЕЛЬНОЙ ДЕФОРМАЦИИ БЕТОНА В РАСТЯНУТОЙ ЗОНЕ ИЗГИБАЕМОГО ЖЕЛЕЗОБЕТОННОГО ЭЛЕМЕНТА // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16844 (дата обращения: 23.02.2026).



