Развитие систем автономного электроснабжения обусловлено целым рядом обстоятельств: необходимость решения социально-экономических проблем в труднодоступных районах, повышенные требования потребителя к независимости от централизованного энергоснабжения и его надежности, возможность или необходимость использовать местные первичные источники производства энергии. Указанная тенденция развития автономных энергетических систем характерна для всей мировой экономики, включая промышленно развитые страны, независимо от климата. Значимость этого явления для России отражена в создании Технологической платформы «Малая распределенная энергетика» [1, 2].
Отметим, что понятие малая электростанция (МЭ) включает в себя: электростанции не свыше 30 МВт мощности, состоящие из агрегатов мощностью не более 10 МВт. В свою очередь малые электростанции делятся на три подкласса: микро-электростанции - не более 100 кВт мощности; диапазон мощностей от 100 кВт до 1 МВт относят к мини-электростанциям; свыше 1 МВт – малые электростанции.
В настоящее время малая электроэнергетика России состоит из более 49000 малых электростанций общей мощностью более 17 млн. кВт, что для России составляет более 8% всей установленной мощности электростанций. Здесь учтены электростанции в составе энергосистем и работающие автономно. Доля производства электроэнергии малыми электростанциями России превышает 5% от общего объема производства электроэнергии в стране. Малые электростанции имеют в среднем установленную мощность около 340 кВт [1,2,4].
Укажем на факторы формирующие тенденции развития малой энергетики в России [1,2,3,4,12]:
- рост благосостояния народонаселения приводит к появлению небольших поселений требующих энергоснабжения, причем зачастую экономически более выгодно создавать автономное энергоснабжение;
- неуклонное перемещение сырьевого сектора в регионы с неразвитой инфраструктурой и территориально удаленные от «центра» России и соответственно от централизованных систем энергоснабжения;
- увеличение доли энергоемких перерабатывающих предприятий;
- рост числа новых энергоемких технологических процессов (добыча высоковязких нефтей, разработка истощенных месторождений);
- рост составляющей стоимости электрической энергии в структуре себестоимости изделий выпускаемых в реальном секторе экономики;
- увеличение среднего срока находящегося в эксплуатации оборудования региональных электрических сетей и действующих электростанций;
- значительная часть территории России (около 70%) находится в зоне децентрализованного энергоснабжения;
- наличие крупных анклавов требующих решения проблем утилизации попутного нефтяного газа, утилизации отходов лесной промышленности;
- необходимость решения задач энергетической безопасности сраны в целом и ее отдельных регионов.
В свою очередь, развитие малой энергетики и расширение использования дизельных электростанций ведет к росту потребления дизельного топлива, соответственно к появлению экологических, логистических и других проблем.
Указанные обстоятельства делают актуальным целый спектр задач [2,5,6,7,8]:
-
Создание методик оптимального размещения малых электростанций.
-
Создание малых электростанций адаптированных к местным энергетическим ресурсам.
-
Создание методик проектирования элементов электротехнических комплексов малой энергетики оптимальных в смысле энергоэффективности.
-
Создание методик и вычислительных инструментов анализа электротехнических комплексов.
-
Создание электротехнических комплексов, на базе дизельных электростанций, минимизирующих расход ресурсов при сохранении качества и надежности поставляемой энергии.
-
Создание многокомпонентных, в смысле видов первичных источников энергии, автономных систем энергоснабжения.
-
Создание систем повышения квалификации и переподготовки кадров в области малой энергетики.
Решение сформулированных выше задач требует создания набора математических моделей малых электростанций, автономных электроэнергетических систем и их элементов. Степень локализации и детализации, при математическом моделировании автономных электроэнергетических систем с дизельными электростанциями (АЭЭС), определяется требуемым уровнем адекватности сформулированных выше задач с одной стороны, и находящимся в руках исследователя инструментом расчета, с другой стороны. К настоящему времени создан широкий спектр моделей и методов извлечения информации из них [9,10]. Различия в исходных теоретических положениях и уровнях допущений принятых при построении отельных математических моделей затрудняет сопоставление результатов.
В направлении разрешения выявленного противоречия предлагается подход базирующийся на формализме Лагранжа [9,11].
Формализм Лагранжа, примененный в целях создания математической модели АЭЭС или ее элементов, требует предварительной структуризации анализируемого комплекса. Ключевым при этом становится представление исследуемой системы в виде совокупности из P элементарных систем, каждая из которых физически однородна. Под физически однородной элементарной системой, в настоящей работе, понимается часть системы в которой происходит преобразование энергии только одного вида (тепловая, механическая, гидравлическая, электрическая, магнитная и др.). Данные элементарные системы взаимно влияют друг на друга и взаимодействуют между собой. Заметим, что «границы» между элементарными системами условны и могут не совпадать с физическими границами рассматриваемого объекта или его конструктивных элементов.
Соответственно приходим к системе уравнений Лагранжа вида
![]() , (1)
, (1)
![]() , (2)
, (2)
где m = 1(1)M.
Запишем систему (1), (2) в более компактном виде (после переобозначений), как дифференциально-алгебраическую систему уравнений, где 2М дифференциальных и 2М алгебраических уравнений, называемую в дальнейшем канонической [11]:
![]() , (3)
, (3)
![]() , (4)
, (4)
где QΣ и Qb векторы обобщенных координат и обобщенных скоростей.
Уравнения (3), (4) обладают следующими характеристиками: их форма свойственна для математической модели АЭЭС в целом; процедура подстановки алгебраической части (4) в уравнения производной (3) требует введения в рассмотрение матрицы Якоби A*(QΣ, Qb) =![]() , суть матрицы динамических параметров. Блочно-диагональная структура матрицы A*(QΣ, Qb) определена наличием P элементарных систем составляющих модель АЭЭС, что обусловливает необходимость процедуры обращения указанной матрицы при переходе к записи модели в нормальной форме Коши. Процедура обращения матрицы A* весьма трудоемка и занимает большую часть времени счета численного метода примененного в случае приведения модели к нормальной форме Коши. Моделирование уравнениями (3), (4) элементарных систем, находящихся во взаимодействии, и обладающих различными постоянными времени, переводит полученную систему уравнений в класс жестких и особо жестких систем. Решение таких систем уравнений требует наличия арсенала специализированных численных методов, способны «учесть» в своей конструкции разброс величин постоянных времени элементарных систем математической модели АЭЭС достигающий 108-1012. Необходимо отметить и «большую» размерность системы уравнений (3)-(4), a поскольку все элементарные системы взаимосвязаны и взаимозависимы, то затруднено прямое применение приемов диакоптики и, для понижения размерности, требуется введение допущений ведущих к снижению степени адекватности модели в целом.
, суть матрицы динамических параметров. Блочно-диагональная структура матрицы A*(QΣ, Qb) определена наличием P элементарных систем составляющих модель АЭЭС, что обусловливает необходимость процедуры обращения указанной матрицы при переходе к записи модели в нормальной форме Коши. Процедура обращения матрицы A* весьма трудоемка и занимает большую часть времени счета численного метода примененного в случае приведения модели к нормальной форме Коши. Моделирование уравнениями (3), (4) элементарных систем, находящихся во взаимодействии, и обладающих различными постоянными времени, переводит полученную систему уравнений в класс жестких и особо жестких систем. Решение таких систем уравнений требует наличия арсенала специализированных численных методов, способны «учесть» в своей конструкции разброс величин постоянных времени элементарных систем математической модели АЭЭС достигающий 108-1012. Необходимо отметить и «большую» размерность системы уравнений (3)-(4), a поскольку все элементарные системы взаимосвязаны и взаимозависимы, то затруднено прямое применение приемов диакоптики и, для понижения размерности, требуется введение допущений ведущих к снижению степени адекватности модели в целом.
Сохранить высокую степень адекватности исходных математических моделей АЭЭС и при этом избежать чрезмерных затрат времени счета, можно конструируя проблемно-ориентированные численные методы, непосредственно применимые к исходной математической модели (3)-(4) представляющей собой систему дифференциальных и алгебраических уравнений.
В дальнейшем под методом интегрирования системы уравнений (3)-(4) будем понимать совокупность состоящую из следующих компонент:
-
Формула интегрирования (может быть несколько формул объединенных вычислительной структурой метода).
-
Схема решения системы нелинейных уравнений, если используются неявные методы при интегрировании системы уравнений (3)-(4).
-
Формула расчета оценки погрешности решения системы уравнений (3)-(4) на одном шаге интегрирования (локальная погрешность - в смысле определений G.Hall, J.M.Watt).
-
Формула расчета оценки глобальной погрешности решения системы уравнений (3)-(4) (глобальная погрешность - в смысле определений G.Hall, J.M.Watt).
-
Стратегия выбора формулы интегрирования на шаге интегрирования, если используется несколько формул объединенных вычислительной структурой метода.
-
Стратегия выбора величины шага интегрирования при интегрировании системы уравнений (3)-(4).
-
Стратегия завершения вычислений при интегрировании системы уравнений (3)-(4).
В данном направлении, для решения задачи (3)-(4), предлагается модификация канонического многошагового метода, которую в дальнейшем будем называть «Многошаговый канонический параллельный метод 2-2-2» (МКПМ 2-2-2).
Отметим, что канонические многошаговые методы – суть частные вариации обобщенного многошагового метода в смысле определений G.Hall, J.M.Watt:
Базовая формула для построения МКПМ 2-2-2 – формула канонического метода – двухшагового, неявного, А – устойчивого, второго порядка точности [11]:
![]()
![]() (5)
(5)
где:
h – шаг интегрирования;
a неяв и β2 неяв –свободные параметры метода;
β0 неяв=β0 неяв (a неяв, β2 неяв) и β1 неяв =β1 неяв (a неяв, β2 неяв)- параметры метода,
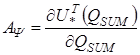 ;
; 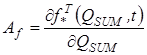 - матрицы.
- матрицы.
Подстановкой β2 неяв=0 в выражение (5) получим полуявный А – устойчивый метод, где при «a» свободном: β0=β0(a); β1=β1(a).
Расчет задачи (3)-(4) ведем параллельно неявным и полуявным методами. Шаг интегрирования h принимается равным для обоих методов и меняется синхронно в зависимости от оценки глобальной погрешности и стратегии выбора шага. Типы поведения глобальных погрешностей, в общем случае, здесь различные, что дает дополнительные гарантии проведения расчета с достоверной оценкой контролируемой глобальной погрешности.
Для повышения точности оценки глобальной погрешности, на каждом шаге интегрирования из точки tn+1 до точки tn+2, с начальными условиями соответствующими tn+1, проводится уточняющий расчет по формуле (5) при β2 неяв=0 с шагом hn+1=h/2, причем в этом случае набор параметров a, β0=β0(a) и β1=β1(a) обеспечивает расширенные области точности и свойство слабой устойчивости формулы (5).
При этом вводится допущение, что на интервале от tn+1 до tn+2 матрицы 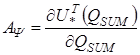 и
и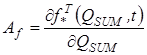 постоянны. Соответственно, при уточняющем расчете с уменьшенным в два раза шагом интегрирования, отпадает необходимость перевычислять обратную матрицу в (5), что позволяет с малыми дополнительными вычислительными затратами получить оценки глобальной погрешности в точке tn+2. Управление величиной шага интегрирования h ведется по максимальному значению оценки глобальной погрешности, таким образом, чтобы она стремилась «снизу» к определённому, наперед заданному значению.
постоянны. Соответственно, при уточняющем расчете с уменьшенным в два раза шагом интегрирования, отпадает необходимость перевычислять обратную матрицу в (5), что позволяет с малыми дополнительными вычислительными затратами получить оценки глобальной погрешности в точке tn+2. Управление величиной шага интегрирования h ведется по максимальному значению оценки глобальной погрешности, таким образом, чтобы она стремилась «снизу» к определённому, наперед заданному значению.
Тестирование предложенного метода проводилось на задаче содержащей 10 дифференциальных и 10 алгебраических уравнений в канонической форме, по структуре соответствующих математической модели электромеханического преобразователя энергии, и имеющих аналитическое решение. Полученные численные решения сравнивались с аналитическими и с численными, полученными ранее известным методом БКМ [11].
Применение разработанного метода к комплексу тестовых задач в канонической форме показало:
1. Глобальная погрешность численного решения на интервале рассмотрения не превышает заранее заданного значения 10-2.
2. Число шагов численного интегрирования на интервале рассмотрения снизилось на 7%, по сравнению с ранее известной программой БКМ.
Выводы
На основании проведенного анализа выявлен спектр актуальных задач математического моделирования, применительно к автономным электроэнергетическим системам. Построен проблемно-ориентированный численный метод, обладающий повышенной точностью оценки глобальной погрешности. Приведен пример применения построенного численного метода. Показано: на тестовой задаче глобальная погрешность численного решения методом МКПМ 2-2-2 не превышает заранее заданного значения; число шагов метода МКПМ 2-2-2 на интервале рассмотрения снизилось на 7%, по сравнению с ранее известным методом БКМ.
Рецензенты:
Харламов В.В., д.т.н., профессор, заведующий кафедрой «Электрические машины и общая электротехника», ФГБОУ ВПО «ОмГУПС», г. Омск;
Кутышкин А.В., д.т.н., профессор, кафедра «Проектирование технологических машин» ФГБОУ ВПО «НГТУ», г.Новосибирск.
Библиографическая ссылка
Архипова О.В., Архипова О.В., Ковалев В.З., Ремизов П.Н. МОДЕЛИРОВАНИЕ АВТОНОМНЫХ ЭНЕРГЕТИЧЕСКИХ СИСТЕМ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16838 (дата обращения: 13.03.2026).



