Энергоснабжение – важнейший аспект функционирования любого производства. Стабильная подача необходимой для реализации технологических процессов энергии определяет стабильность работы предприятий. Вопросы надёжности и эффективности энергоснабжения приобретают особое значение для предприятий, имеющих на своём балансе удалённые от централизованной энергосистемы объекты (например, газо- и нефтепроводы большой протяженности). Как правило, функционирование таких объектов сопровождается необходимостью размещения мелких линейных объектов, таких как устройства электрохимзащиты, крановые узлы, пункты телемеханики и др. Если газо- или нефтепроводы расположены на территориях, удалённых от централизованной энергосистемы, единственно возможным способом организации энергоснабжения является применение автономных источников.
Для энергообеспечения газопроводов Российского Дальнего Востока применяются автономные источники энергии с замкнутым термодинамическим циклом мощностью до 4 кВт (рис. 1). Такие источники работают на природном газе и характеризуются значительной длительностью работы в автоматическом режиме и высоким значением термического кпд. Тем не менее, часто происходят отказы в работе этого оборудования, которые негативно сказываются на функционировании газотранспортной системы. При этом анализ статистических данных показал [2], что одной из основных причин нарушений работы энергоисточника являются предельно высокие значения температуры рабочего вещества на выходе из конденсатора.
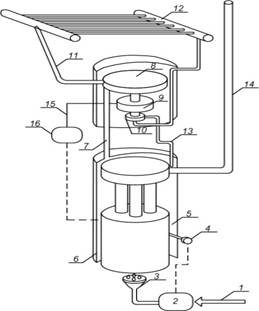
Рис. 1. Схема энергоустановки, работающей по замкнутому циклу пара: 1 – подвод топлива; 2 – панель управления подачей горючего; 3 – горелка; 4 – термостат;
5 – органическая жидкость; 6 – парогенератор; 7 – пар; 8 – турбина; 9 – генератор переменного тока; 10 – насос; 11 – подача пара в конденсатор; 12 – конденсатор; 13 – вывод конденсата; 14 – дымовая труба; 15 – кабели входа переменного тока к выпрямителю;
16 – электрический щит.
Цель исследования – анализ режимов работы автономных энергоустановок, при которых возникают отказы в связи с предельно высокой температурой в конденсаторе, а также определение наработки на отказ с учётом климатических условий Дальнего Востока России.
Постановка задачи
Энергоустановка (рис. 1) функционирует по следующему принципу. Горелка 3, работающая на природном газе, в парогенераторе 6 нагревает, а затем испаряет органическое рабочее вещество (дихлорбензол). Рабочее вещество в парообразном состоянии подаётся в турбину 8 и приводит во вращение вал турбогенератора переменного тока 9. Далее рабочее вещество поступает в конденсатор с воздушным охлаждением 12, состоящий из 2 рядов оребрённых трубок внутренним диаметром Din=38 мм, объединённых коллекторами. Рабочее вещество конденсируется, насосом 10 возвращается в парогенератор 6, и цикл замыкается. Следует отметить, что дихлорбензол помимо использования в рабочем цикле энергоустановки является также жидкостью, смазывающей подшипники скольжения вала турбогенератора.
Предполагалось, что дихлорбензол в парообразном состоянии при температуре насыщения TS поступает в трубки конденсатора (рис. 2). Через стенки трубок происходит теплоотвод от рабочего вещества окружающему воздуху, сопровождающийся охлаждением и конденсацией паров дихлорбензола. На внутренней поверхности трубок конденсатора образуется плёнка, толщина которой по мере течения парожидкостной смеси внутри канала увеличивается. Процесс конденсации завершается при достижении доли пара в парожидкостной смеси рабочего вещества нормативного значения, заявленного заводом-изготовителем [4].
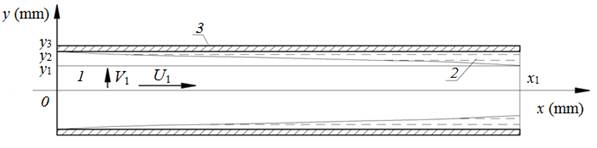
Рис. 2. Схема области решения задачи: 1 – пары рабочего вещества; 2 – конденсат; 3 – стенка трубки конденсатора;
4 – окружающий воздух.
Математическая модель
Нестационарные дифференциальные уравнения, описывающие процесс конденсации рабочего тела в трубках конденсаторной установки (рис. 2) и соответствующие сформулированной физической постановке задачи, имеют следующий вид.
Уравнение теплопроводности для рабочего вещества в зоне конденсации (T1=Ts, 0<x<x1, 0<y<y1):
![]() . (1)
. (1)
Уравнение теплопроводности для рабочего вещества вне зоны конденсации (Т1<Тs, 0<x<x1, y1<y<y2):
![]() . (2)
. (2)
Уравнение теплопроводности для стенки (0<x<x, y2<y<y3):
![]() . (3)
. (3)
Уравнение диффузии паров рабочего вещества (0<x<x1, 0<y<y1):
![]() . (4)
. (4)
Уравнение движения паров рабочего вещества (0<x<x1, 0<y<y1):
![]() . (5)
. (5)
Уравнение неразрывности паров рабочего вещества (0<x<x1, 0<y<y1):
![]() . (6)
. (6)
Уравнение состояния паров рабочего вещества (0<x<x1, 0<y<y1):
![]() . (7)
. (7)
Здесь T – температура, К; t – время, с; x, y – координаты декартовой системы координат, м; U, V – компоненты скорости в проекции на оси x и y, м/с; a – коэффициент температуропроводности, м2/с; Cv – молярная концентрация, моль/м3; D – коэффициент диффузии, м2/с; ρ – плотность, кг/м3; P – давление, Н/м2; μ – коэффициент динамической вязкости, кг/(мс); M – молярная масса, кг/моль; Rt – универсальная газовая постоянная, Дж/(моль·К); Т0 – начальная температура, К; λ – коэффициент теплопроводности, Вт/(м·К); Qc – скрытая энергия фазового перехода, Дж/кг; Wc – скорость конденсации, кг/(м2·c); α – коэффициент теплоотдачи, Вт/(м2·К); Тout – температура окружающей среды, К; Tinput – температура паров на входе в канал, К; U0, V0 – начальные распределения скорости, м/с; C0 – концентрация пара на входе в канал (C0=ρ1input/M1), моль/м3; ρ1input – плотность пара на входе в канал, кг/м3; β – безразмерный коэффициент конденсации (β=0,1); kβ – дополнительный коэффициент, равный 0,4; Pn – давление насыщенных паров, Н/м2; индексы «1», «2», «3» соответствуют парам дихлорбензола, его жидкой фазе и материалу труб конденсатора.
Система нестационарных дифференциальных уравнений с соответствующими граничными условиями (1)–(8) решалась методом конечных разностей [5, 6]. Разностные аналоги дифференциальных уравнений (1)–(8) решались локально–одномерным методом. Для решения одномерных разностных уравнений применялся метод прогонки с использованием неявной четырехточечной схемы. Для решения нелинейных уравнений применялся метод простых итераций. Методика оценки достоверности результатов выполненных численных исследований основана на проверке консервативности применяемой разностной схемы.
Результаты и обсуждение
Численные исследования выполнены при типичных значениях параметров работы рассматриваемых конденсаторных установок автономных источников энергоснабжения (рис. 2): начальная температура рабочего вещества на входе в конденсатор T1 = 403 К; тепловой эффект конденсации дихлорбензола Qc = 311.7 кДж/кг; размеры области решения Hx = 400 мм, Hy = 1500 мм; молекулярная масса дихлорбензола M = 147 кг/кмоль; безразмерный коэффициент испарения β = 0.1; скорость движения рабочего тела в конденсаторе V1 = 0.01 м/с; коэффициент теплоотдачи при конденсации паров дихлорбензола в канале конденсатора α1-2 = 650 Вт/(м2∙К).
Теплофизические характеристики дихлорбензола, стали, воздуха приведены в [1, 7, 8].
На рис. 3 представлены зависимости температуры дихлорбензола на выходе из конденсатора Toutput от входной температуры рабочего вещества Tinput при разных значениях температуры окружающего воздуха. Необходимо отметить, что температура рабочего вещества на входе в конденсатор непосредственно связана с выходной электрической мощностью энергоустановки.
При этом критическим значением температуры дихлорбензола на выходе из конденсатора, при превышении которого риск возникновения отказа в работе автономного источника энергоснабжения значительно возрастает, является Toutput ≈ 340 К. На основании полученных результатов численного моделирования можно сделать вывод, что при температуре наружного воздуха Tout = 303 K критическое значение температуры рабочего вещества после конденсатора достигается уже при входной температуре Tinput≈420 К, что соответствует мощности P=1500 Вт (менее 40% от номинальной).
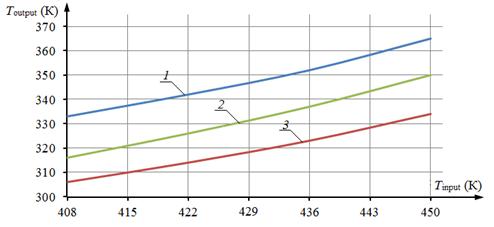
Рис. 3. Значения выходной температуры рабочего потока Toutput при различных значениях температуры на входе в конденсатор Tinput:
1 – Tout = 303 K; 2 – Tout = 273 K; 3 – Tout = 253 K.
В результате проведённых численных исследований определена зависимость температуры рабочего тела на выходе из конденсатора от температуры окружающего конденсатор воздуха при различных режимах работы (таблица). Полученные зависимости хорошо соответствуют данным, представленным на рис. 3.
Таблица Зависимость температуры дихлорбензола на выходе из конденсатора от температуры окружающего воздуха.
|
Tout (K) |
253 |
263 |
273 |
283 |
293 |
303 |
313 |
|
При температуре на входе в конденсатор Tinput=403 К |
|||||||
|
Toutput (K) |
306 |
309 |
313 |
317 |
323 |
330 |
337 |
|
При температуре на входе в конденсатор Tinput=426 К |
|||||||
|
Toutput (K) |
314 |
318 |
322 |
326 |
332 |
338 |
346 |
|
При температуре на входе в конденсатор Tinput=447 К |
|||||||
|
Toutput (K) |
334 |
338 |
344 |
348 |
354 |
362 |
369 |
Результаты численных исследований позволяют определить наработку на отказ рассматриваемых автономных источников энергоснабжения при эксплуатации в конкретных климатических условиях. В качестве примера можно рассмотреть Амурскую область России, протяжённость магистральных газопроводов по территории которой составляет более 1200 км. Данные, представленные на рис. 3 и в таблице позволяют сделать вывод о том, что при функционировании автономной энергоустановки на номинальной мощности (Р = 2000 Вт, Tinput=426 К) температура рабочего вещества на выходе из конденсатора превысит критическое значение при температуре наружного воздуха около 303 К. По данным многолетних климатических наблюдений [3] в Амурской области продолжительность погодных условий с температурой воздуха 300 К и выше в течение года составляет 840 ч. Таким образом, время наработки на отказ при мощности Р = 2000 Вт в климатических условиях Амурской области составит 7920 ч.
Следует отметить, что климатические условия региона, рассматриваемого в качестве примера для расчета времени наработки на отказ, характеризуются большой продолжительностью периодов с пониженной температурой воздуха. В случае использования рассматриваемых автономных энергоустановок в регионах центральной части России или в странах Европы с более теплым климатом и большей продолжительностью периодов времени с повышенной температурой воздуха показатели надежности работы автономного источника энергоснабжения могут быть значительно снижены.
Заключение
Разработана математическая модель, позволяющая прогнозировать возникновение отказов в работе автономного источника энергоснабжения с замкнутым термодинамическим циклом при работе в широком диапазоне выходной мощности и в различных климатических условиях. В результате проведенных численных исследований процесса конденсации рабочего вещества (дихлорбензола) в воздушном конденсаторе автономного источника энергоснабжения с замкнутым термодинамическим циклом получены зависимости выходной температуры рабочего вещества от его начальной температуры и от температуры окружающего воздуха.
Работа выполнена в рамках НИР Госзадания «Наука» (Шифр Федеральной целевой программы 2.1321.2014).
Рецензенты:
Литвак В.В., д.ф.-м.н., профессор каф. Атомных и тепловых электростанций НИ ТПУ, г. Томск;
Стрижак П.А., д.ф.-м.н., профессор каф. Автоматизации теплоэнергетических процессов НИ ТПУ, г. Томск.
Библиографическая ссылка
Пискунов М.В., Войтков И.С., Высокоморная О.В., Высокоморный В.С. ПОКАЗАТЕЛИ НАДЕЖНОСТИ АВТОНОМНЫХ ИСТОЧНИКОВ ЭНЕРГОСНАБЖЕНИЯ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16775 (дата обращения: 23.02.2026).



