Статья посвящена численному решению задачи синтеза системы управления. Синтез системы управления обеспечивает нахождение функции, описывающей зависимость управления от координат пространства состояний объекта. Рассматривается задача синтеза робастной системы управления, в которой модель объекта управления имеет множество неопределенных параметров. С целью обеспечения свойства робастности множество неопределенных параметров покрывается сеткой определенных значений. Для решения задачи применяется метод сетевого оператора [1,2,5], который использует кодирование математического выражения в форме целочисленной матрицы. Метод сетевого оператора относится к классу современных методов символьной регрессии. Все эти методы производят поиск оптимального решения в форме кода с помощью эволюционных алгоритмов [4]. Эффективность этих алгоритмов определяется мощностью начального множества возможных решений и количеством циклов преобразования этого множества. В рассматриваемой задаче множество неопределенных значений существенно усложняет процесс поиска решения. Для повышения эффективности метода сетевого оператора применяются параллельные технологии создания алгоритмов. В работе представлен анализ параллельных алгоритмов метода сетевого оператора. Рассматриваются подходы, обеспечивающие параллельное вычисление функционалов на множестве значений неопределенных параметров и параллельное вычисление вариаций для множества базисных решений [3,7-9]. Рассматривается пример синтеза робастной системы управления спуском космического аппарата (КА) на поверхность Луны.
Задача численного синтеза робастного управления
Модель объекта управления задана системой обыкновенных дифференциальных уравнений:
![]() , (1)
, (1)
где функция ![]() - вектор-функция с векторными аргументами, х – вектор состояния,
- вектор-функция с векторными аргументами, х – вектор состояния, ![]() , u – вектор управления,
, u – вектор управления, ![]() ,
, ![]() , y – вектор неопределенных параметров,
, y – вектор неопределенных параметров, ![]() ,
, ![]() - замкнутые и ограниченные множества.
- замкнутые и ограниченные множества.
Для системы (1) заданы начальные условия, значения которых могут зависеть от неопределенных параметров:
![]() (2)
(2)
где х0 – вектор заданных начальных значений.
Заданы терминальные условия:
![]() , (3)
, (3)
где tf – время процесса управления определяется из соотношения:
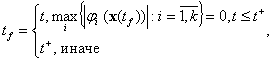 (4)
(4)
где ![]() задано и определяет верхнюю границу возможного времени управления.
задано и определяет верхнюю границу возможного времени управления.
Задан функционал качества:
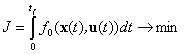 , (5)
, (5)
Необходимо найти функцию управления в виде:
![]() (6)
(6)
где ![]() - вектор-функция
- вектор-функция ![]() со следующими свойствами:
со следующими свойствами:
![]() ,
,
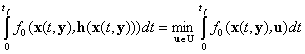 , (7)
, (7)
![]() ,
,
где ![]() - решение системы дифференциальных уравнений
- решение системы дифференциальных уравнений ![]() ,
,![]() .
.
Для решения данной задачи (1-6) используем численный метод сетевого оператора. Множество неопределенных параметров заменяем конечным множеством определенных значений из заданного множества:
![]() . (8)
. (8)
Заменяем терминальные условия (3) дополнительным функционалом, а функционал качества (5) заменяем суммой функционалов, вычисленных для каждой точки из множества неопределенных параметров (8). В результате получаем задачу многокритериальной оптимизации с критериями:
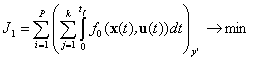 , (9)
, (9)
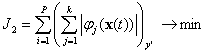 . (10)
. (10)
Метод сетевого оператора
Метод сетевого оператора был описан во многих работах [1,2,5]. Метод сетевого оператора позволяет представить математическое выражение в виде целочисленной матрицы, что дает больше гибкости при программировании данного метода. В данной работе не производится никаких аналитических изменений в исходной постановке задачи, однако в данном случае выбраны неопределенные параметры объекта, значения которых задаются множеством точек в заданном интервале. Данное преобразование придает свойство робастности системе управления. При этом функционалы высчитываются для каждой точки из множества неопределенных параметров, а результирующим считается сумма функционалов по всем точкам каждого параметра. В данной работе применяется параллельная реализация метода сетевого оператора. Такая реализация позволяет рассмотреть большее количество возможных решений без существенного увеличения временных затрат, а соответственно, шанс найти необходимое решение возрастает. Также в данной реализации предоставляется возможность сократить время всего алгоритма за счет распараллеливания процесса вычисления функционалов.
Принципы распараллеливания
Поисковая часть метода сетевого оператора основана на генетическом алгоритме. Существует несколько моделей распараллеливания генетических алгоритмов [7-9], из них три основных, а остальные являются их расширениями и комбинациями:
1. Master-slave (ведущий-ведомый) модель. Модель, при которой основной поток (ведущий, master) обрабатывает единственную популяцию. Таким образом, весь генетический алгоритм производится master-потоком. Остальные потоки (ведомые, slave) лишь получают от master-потока задания на расчет значений критериев (функционалов). В силу существования ведущего и ведомых потоков, данную модель часто называют master-slave моделью (ведущий-ведомый). Такая модель особенно эффективна, если критерии описываются сложными математическими выражениями;
2. Клеточная модель. В данной модели популяция разбивается на мелкие части (клетки). Такая модель часто именуется выражение «мелкозернистый» параллелизм (fine grained parallelism). Основной идеей данной модели является разделение популяции на мелкие группы хромосом (обычно по одной или две). Таким образом, хромосомы могут взаимодействовать только внутри своей подгруппы;
3. Распределенная модель. В данной модели популяция также разбивается на части, но не настолько мелкие, как в клеточной модели. Поэтому данная модель также носит название «крупнозернистый» параллелизм (coarse grained parallelism). Субпопуляции, полученные после разбивки основной популяции, могут обмениваться своими хромосомами (процесс миграции). Субпопуляции часто называют островами, из-за чего сама модель часто именуется также и островным подходом или островной моделью параллелизма.
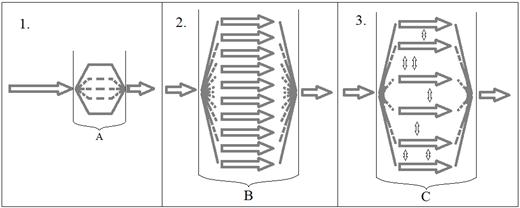
Рис.1. Три подхода распараллеливания. А – часть алгоритма, вычисляющая значения функционалов; В – часть алгоритма, в которой выполняются генетические алгоритмы в каждой субпопуляции в отдельной потоке; С - часть алгоритма, в которой выполняются генетические алгоритмы в каждой субпопуляции в отдельном потоке, при этом они могут обмениваться хромосомами
Существуют гибридные (смешанные) модели распараллеливания генетических алгоритмов [7], которые основаны на одной из трех вышеописанных моделей, однако вбирают в себя некоторые принципы остальных моделей. Например, модель ведущий-ведомый разделяют на синхронную и асинхронную. Разница заключается в наличии возможности продолжения вычислений ведущим потоком без ожидания ведомых. Распределенную модель с миграциями иногда разделяют на островную модель и модель ступенек. Разница состоит в том, что при островной модели миграции хромосом могут происходить между любыми субпопуляциями (мигранты, путешествующие по островам), а при модели ступенек миграция происходит только между соседними субпопуляциями.
Иногда процедуру миграции полностью исключают из алгоритма, но вместо этого включают понятие пересекающихся областей субпопуляций. Тогда в процессе исполнения алгоритма в операции скрещивания внутри одной субпопуляции могут попасть хромосомы из области общего доступа. Так решается проблема обмена между субпопуляциями.
Существует так называемые грязные генетические алгоритмы, для которых также существуют параллельные реализации. Чаще всего грязный генетический алгоритм имеет два цикла: внешний и внутренний. Основная параллельная область исполняется на стадии внутреннего цикла, но внешний цикл также поддается распараллеливанию, однако это зависит от реализации алгоритма.
Самым простым подходом распараллеливания генетических алгоритмов считается подход изолированного исполнения. Алгоритм реализуется так, что на каждом отдельном процессоре или ядре полностью исполняется последовательный алгоритм. Таким образом, на многопроцессорной системе запускается сразу несколько последовательных алгоритмов, которые никак не связаны друг с другом. Соответственно, после того, как каждый процессор завершит вычисления, будет получено большее множество возможных решений, чем при работе лишь одной копии алгоритма.
Синтез системы управления посадкой КА на поверхность Луны
Эксперимент проводился на модели КА, движение которого задано системой из пяти дифференциальных уравнений (1-4):
![]()
![]()
![]() , (11)
, (11)
![]()
![]()
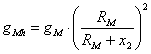 , (12)
, (12)
где x0 – скорость движения КА в текущий момент времени, x1 – угол наклона траектории КА в текущий момент времени, x2 – высота полета КА относительно поверхности Луны в текущий момент времени, x3 – дальность полета КА на текущий момент времени, x4 – масса КА с учетом топлива, gE – значение ускорения свободного падения на Земле, gM – значение ускорения свободного падения на поверхности Луны, gMh – значение ускорения свободного падения на некоторой высоте над поверхностью Луны, P0c – номинальная тяга двигателя КА (кг), Pudc – удельная тяга двигателя КА (с), RM – радиус Луны; u0 – управление углом наклона траектории, ![]() , u1 – управление тягой двигателя КА,
, u1 – управление тягой двигателя КА, ![]() .
.
Начальные условия заданы следующим образом:
Таблица 1
Начальные условия
|
Угол наклона траектории |
Начальная масса с учетом топлива |
Начальная скорость |
Начальная высота |
Начальное отклонение угловой дальности |
|
|
|
|
|
|
Терминальные условия заданы следующим образом:
· Конечная скорость: 0 м/с;
· Конечная высота: 1.5 км.
Функционал качества и функционал цели управления для данной системы заданы в следующем виде:
![]() , (13)
, (13)
![]() , (14)
, (14)
где ν1 = 0.1, ν2 = 0.1 весовые коэффициенты. В отличие от [2] в данном эксперименте использовался функционал с учетом дальности отклонения от планируемой точки посадки.
Для данного эксперимента в качестве неопределенных параметров выбраны начальная высота, с которой начинается процесс посадки и начальный угол наклона КА. Начальная высота рассчитывается как точка перицентра Луны (периселений), но для обеспечения робастности системы рассматривается конечное множество точек, в котором может находиться КА. Начальный угол наклона КА может также отличаться от заданного и, соответственно, задается конечным множеством точек:
![]() , (15)
, (15)
![]() , (16)
, (16)
где y1 – отклонение по начальной высоте, y2 – отклонение по начальному углу. Величина l –выбирается в зависимости от величины интервала ![]() или
или ![]() и от необходимой степени робастности по определенному параметру. Однако необходимо учесть, что высокая дискретность данных интервалов влечет за собой увеличение времени расчетов, так как расчеты функционалов производятся для каждой комбинации неопределенных параметров. Таким образом, для случая, когда P = 2 и l = 2, функционалы будут рассчитаны
и от необходимой степени робастности по определенному параметру. Однако необходимо учесть, что высокая дискретность данных интервалов влечет за собой увеличение времени расчетов, так как расчеты функционалов производятся для каждой комбинации неопределенных параметров. Таким образом, для случая, когда P = 2 и l = 2, функционалы будут рассчитаны ![]() раза.
раза.
В данном эксперименте применяется комбинация модели ведущий-ведомый и островной модели распараллеливания. Выбор модели ведущий-ведомый обусловливается необходимостью вычислять функционалы для нескольких точек из области неопределенных параметров. Выбор островной модели обусловливается содержанием большого количества хромосом в каждой популяции. Для достижения большей эффективности распараллеливания применяется комбинация данных моделей. Перед началом работы алгоритма исследователю предлагается выбрать количество процессоров, используемых на распределение по островам. Учитывая данное значение, программа автоматически вычисляет количество оставшихся процессоров, которое используется для вычисления функционалов. Также перед началом работы исследователь задает количество поколений, пар в поколении, эпох (определяет размер цикла поколений, после которого происходит отбор лучшего решения от каждого острова). По прохождении эпохи каждый остров принимает отобранную лучшую хромосому в качестве базисной, и дальнейшая работа происходит именно с ней (миграция хромосом). Каждый остров имеет в своем распоряжении определенное количество процессоров, которые используются для расчета функционалов. Параллельность алгоритма расчета функционалов заключается в независимом расчете значения функционала для каждой точки из множества точек каждого неопределенного параметра. Работа организована по алгоритму, при котором поток, освободившись от вычисления функционала при определенной точке неопределенных параметров, тут же переходит на следующую точку. Соответственно, в таком режиме запускаются сразу несколько потоков. Каждое полученное значение функционала автоматически суммируется к значению функционала для каждой хромосомы. Таким образом, такой процесс заметно ускоряет процедуру расчета функционалов. Параметры генетического алгоритма выглядят следующим образом:
· размер эпохи (количество поколений, после которых происходит обмен): 25;
· количество пар в поколении (количество сгенерированных пар за поколения): 128;
· общее количество поколений: 500;
· размерность каждой популяции (количество хромосом в каждой популяции):1000;
|
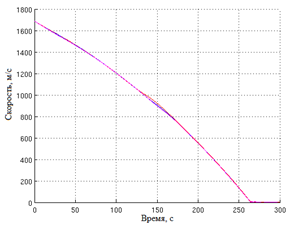
Рис.2. Изменение скорости. |
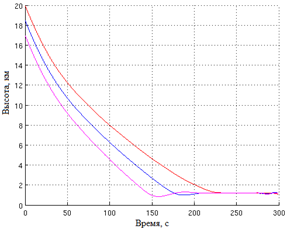
Рис.3. Изменение высоты при разных НУ. |
На рис. 2 и рис. 3 показаны графики изменения скорости и высоты при разных начальных условиях: ![]() . Таким образом, КА выходит на необходимую высоту с разных начальных условий и достигает на ней нулевую скорость.
. Таким образом, КА выходит на необходимую высоту с разных начальных условий и достигает на ней нулевую скорость.
При тех же параметрах алгоритма был проеден сравнительный анализ времени вычислений, результаты которых представлены ниже.
|
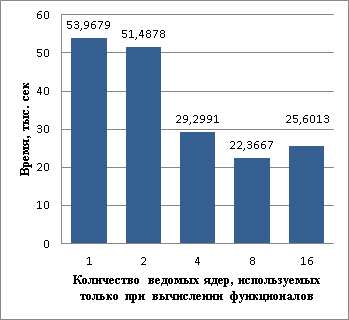
Рис.4. Зависимость времени от количества ведомых ядер |
На рис. 4 показан график зависимости времени выполнения алгоритма от количества ведомых ядер (выделенных на вычисление функционалов) при одних и тех же начальных параметрах. По графику видно, что при увеличении количества ведомых ядер время расчета уменьшается, но лишь до определенного момента. В частности, при выделении 16 ядер на вычисление функционалов, время начинает расти, из-за выделения большего времени на создание и уничтожение потоков. |
Для проведения следующего сравнительного анализа времени использовались следующие параметры генетического алгоритма и распределения ядер:
· размер эпохи (количество поколений, после которых происходит обмен): 10;
· количество пар в поколении (количество сгенерированных пар за поколения): 32;
· общее количество поколений: 16;
· размерность каждой популяции (количество хромосом в каждой популяции): 32;
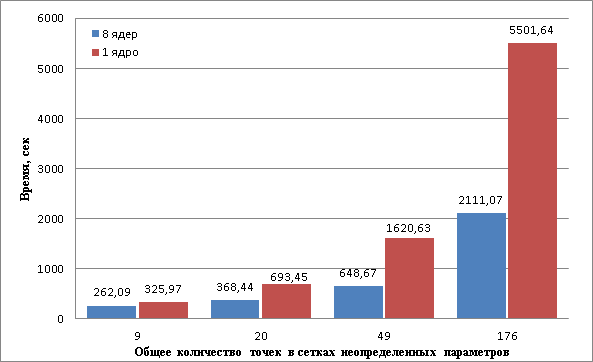
Рис.5. Зависимость времени от размерности сетки неопределенных параметров и количества ведомых ядер.
На рис. 5 показан график зависимости времени от размерности сетки неопределенных параметров и количества ведомых ядер (выделенных на вычисление функционалов). По графику видно, что разница между временем однопоточного и многопоточного вычислений растет с увеличением размерности сетки параметров.
В следующей таблице представлено отношение времени выполнения при 1 ядре к времени при 8 ядрах:
Таблица 2
Отношение времени выполнения при 1 ядре к времени при 8 ядрах
|
Размерность сетки |
3×3 = 9 |
4×5 = 20 |
7×7 = 49 |
16×11 = 176 |
|
Отношение |
1,24 |
1,88 |
2,49 |
2,61 |
Вычисления производились на вычислительной машине HP ProLiant DL785 G5 (8 4-х ядерных процессоров по 2,2 ГГц, 48 ГБ оперативной памяти), работающей на операционной системе Linux Mageia 4 x86_64.
Для решения задачи численного синтеза системы управления посадкой космического аппарата был разработан параллельный метод сетевого оператора, позволяющий рассмотреть большее количество возможных решений, чем при вычислении с использованием одного ядра. Соответственно, это увеличивает шансы нахождения подходящего решения. Разработанный алгоритм позволяет балансировать нагрузку на ядра процессоров, распределяя ее между независимыми базисными потоками и вычислением функционалов для каждой точки из множества неопределенных параметров.
Рецензенты:
Никульчев Е.В., д.т.н., профессор, проректор по научной работе НОУ ВО «Московский технологический институт», г.Москва;
Забудский Е.И., д.т.н., профессор кафедры Электропривод и электротехнологии, ФГБОУ ВПО Российский государственный аграрный университет – МСХА им. К.А. Тимирязева, г.Москва;
Петров М.Н., д.т.н., профессор, профессор кафедры «Системный анализ и исследование операций», Сибирский государственный аэрокосмический университет им. М.Ф. Решетнева, г.Красноярск.
Библиографическая ссылка
Хамадияров Д.Б., Уваров А.С., Дивеев А.И. ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ МЕТОДА СЕТЕВОГО ОПЕРАТОРА ДЛЯ СИНТЕЗА РОБАСТНОЙ СИСТЕМЫ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16770 (дата обращения: 23.02.2026).