Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Газовые инфракрасные излучатели (ГИИ) становятся все более и более перспективными источниками энергии в системах локального теплоснабжения производственных помещений [1, 5]. Но их широкое применение сдерживается тем, что до настоящего времени не разработана теория процессов теплопереноса в областях, подвод теплоты в которые осуществляется при работе ГИИ. Последнее же во многом обусловлено отсутствием экспериментальных данных по температурным полям в зонах воздействия таких излучателей. Одним из основных при этом остается вопрос о механизме передачи энергии в воздухе при работе ГИИ.

Условно область теплопередачи в окрестности ГИИ может быть разделена на три зоны: основная (или рабочая), сохранение температуры воздуха в которой является целью работы излучателей; зона аккумуляции энергии ГИИ и последующего нагрева воздуха; малая окрестность работающих излучателей, в которой температура среды может быть выше предельно допустимой. До настоящего времени не опубликовано достоверных экспериментальных данных по температурным полям каждой из этих зон.  

Целью настоящей работы является экспериментальное изучение закономерностей формирования температурных полей в относительно малой (с характерными размерами до 1,5 м) окрестности газового инфракрасного излучателя и обоснование физической модели теплопереноса в области, нагреваемой ГИИ.

Таблица 1

 Результаты измерений температуры

Расстояние от излучающей поверхности, x,м	Температура, °С
	Номер эксперимента
	1	2	3	4	5	6	7	8	9	10
0,10	354	364	369	355	357	340	349	352	358	352
0,20	305	322	320	334	345	315	322	315	305	317
0,40	280	269	255	257	240	252	240	250	257	250
0,60	200	217	215	229	240	210	217	210	200	212
0,80	214	203	191	193	175	187	175	185	192	185
1,00	152	170	168	170	172	162	170	162	152	172
1,25	147	145	143	145	127	147	127	137	145	137
1,50	98	114	113	114	115	110	114	107	100	115

Экспериментальные исследования проведены на крупногабаритных (характерные размеры более 10 м) моделях объектов теплоснабжения с вертикальными и горизонтальными стенками конечной толщины (ограждающими конструкциями) в условиях низких температур (от - 10 °С до - 30 °С) во внешней по отношению к модели среде. Измерения температур воздуха выполнены в восьми точках на отрезке 1,5 м по поверхности излучения ГИИ (таблица 1). Для обеспечения достоверности результатов измерений эксперименты в идентичных условиях повторялись 10 раз (таблица 1). Измерения выполнялись в условиях установления стационарного распределения температур в области измерений.

По усредненным значениям температуры (таблица 2) вычислен коэффициент корреляции r = -0,971.

Таблица 2

Средние значение температуры

Для определения вида зависимости t(x) применялись методы линейного регрессионного анализа. Корреляционное поле (рис. 1) показывает, что эта зависимость близка к линейной:

,

где  – коэффициент регрессии.

Для определения коэффициентов b0, b1 использован метод наименьших квадратов – сумма квадратов отклонений экспериментальных (эмпирических) значений tэ от их расчетных (теоретических) значений tp была минимальной, т.е.

,

где tp – значение, вычисленное по уравнению регрессии.

Регрессионный анализ позволил установить точечные оценки коэффициентов уравнения регрессии.

Уравнение регрессии имеет вид:

                                                                                                             (1)

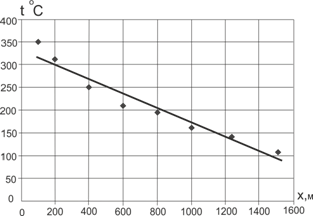
Рисунок 1. Распределение температуры по координате x

Проведена проверка одного из условий Гаусса – Маркова – математическое ожидание отклонений равно нулю для всех наблюдений (таблица 3), (случайные отклонения в среднем не оказывают влияния на зависимые переменные):

Таблица 3

Вычисленные по формуле (1) значения температуры

Коэффициент детерминации полученной модели равен R2 = 0,943.

На следующем этапе обработки результатов экспериментов проверялась возможность представления уравнения регрессии в виде нелинейной зависимости (полинома 2-ой степени).

Уравнение нелинейной регрессии принято в виде:

.

После его линеаризации получено уравнение множественной регрессии:

, где .

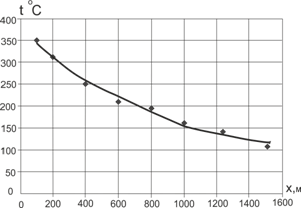
Рисунок 2. Распределение температуры по координате x

Оценки коэффициентов этого уравнения выполнены по методу наименьших квадратов. В результате получено нелинейное выражение в виде

.                                                            (2)

Проведены расчеты отклонений между экспериментальными значениями t и значениями t*, полученными по формуле (2). Установлено, что суммарная погрешность мала (таблица 4):

Таблица 4

 Вычисленные по формуле (2) значения температуры

 

Коэффициент детерминации (R2 = 0,9909) в этом случае оказался выше, чем в линейной модели. Установлено, что при уровне значимости 0,05 все коэффициенты являются статистически значимыми.

Обе модели дают незначительную суммарную погрешность отклонений, но нелинейная регрессионная модель предпочтительнее.

На основании полученных результатов можно сделать вывод о том, что в относительно малой по размерам (около 1,5 м) области вблизи излучающей поверхности газового инфракрасного излучателя температура воздуха изменяется от максимального значения 335 0С (х = 0,1 м) до 110 0С (х = 1,5 м). Такие высокие температуры могут быть следствием только интенсивного прогрева воздуха за счет теплопроводности. Эксперименты проводились в среде очищенного от пыли (которая может поглощать и рассеивать энергию излучения) воздуха. Поэтому повышение температуры в этой области не может быть следствием непосредственного воздействия лучистого потока.

Полученные экспериментальные данные являются основанием для вывода о необходимости учета процессов кондуктивного теплопереноса при анализе температурных полей в области нагрева газовыми инфракрасными излучателями.

Результаты выполненных экспериментальных исследований являются основанием для дальнейшего развития моделей теплопереноса в замкнутых областях, заполненных воздухом и ограниченных стенками конечной толщины, в условиях работы локальных источников нагрева (в том числе газовых инфракрасных излучателей) [2-4]. Установлено, что процессы конвекции в воздухе, несмотря на низкие коэффициенты теплопроводности этого газа, играют важную роль в формировании тепловых режимов областей, нагреваемых за счет потока излучения, поступающего с верхней границы таких областей.

Работа выполнена в рамках НИР Госзадания «Наука» (Шифр Федеральной целевой программы 2.1321.2014).

Рецензенты:

Заворин А.С., д.т.н., зав. каф. Парогенераторостроения и парогенераторных установок НИ ТПУ, г. Томск;

Литвак В.В., д.ф.-м.н., профессор каф. Атомных и тепловых электростанций НИ ТПУ,           г. Томск.