Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

С точки зрения теории оптимального управления лесосушильная камера представляет собой объект с распределенными параметрами [1], который описывается системой дифференциальных уравнений в частных производных (ДУЧП). С некоторыми допущениями низкотемпературную сушку пиломатериалов можно рассматривать [2] как процесс несвязанного тепломассообмена, т.к. он протекает при постоянной температуре и влиянием теплообмена на массоперенос можно пренебречь. В этом случае уравнение переноса для неограниченной пластины имеет вид:

    (0 ≤ x ≤ R,  am = const)                                  (1)

при начальных и граничных условиях:

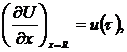
                              (2)

Функция u (τ), рассматриваемая как управляющая, имеет физический смысл плотности потока вещества на поверхности тела. В рассматриваемом случае:

,                                         (3)

где  - состояние агента сушки, определяющее равновесную влажность  древесины;

       аm – коэффициент влагопроводности древесины;

       αm – коэффициент влагообмена.

Вводится ограничение:

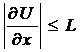          (0 ≤ х ≤ R),                                                (4)

Далее зададим конечное состояние U в виде функции f (x) непрерывной и однозначной на отрезке [0, R].

Пусть U [u (τ), τ, x] – решение уравнения (1) при условиях (2).

Необходимо найти такое управляющее воздействие u (τ)  (0 ≤ τ ≤ T), чтобы при условии (4) выполнялось равенство:

U [u (T), T, x] = f (x),                                                    (5)

причем время Т было бы минимальным. Предполагается также, что такое управляющее воздействие существует.

Рассмотрим один из возможных вариантов приближенного решения и дадим оценку получаемой при этом погрешности вида:

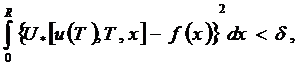                                          (6)

где  U* - приближенное решение;

        δ – заданная допустимая погрешность.

Продифференцируем уравнение (1) по х:

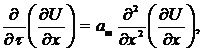                                                              (7)

Из (7) следует, что  удовлетворяет однородному уравнению теплопроводности. На основании теоремы о наибольшем и наименьшем значениях решения уравнения теплопроводности [3] можно заключить, что если в начальный момент τ = 0 справедливо

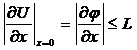,        (0 ≤ х ≤ R),

а в последующее время τ > 0  выполняется неравенство

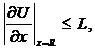
то имеет место неравенство

 при  τ ≥ 0   (0 ≤ х ≤ R).

Таким образом, ограничение (4) можно заменить ограничением

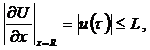                                                          (8)

Далее применим конечное интегральное косинус–преобразование по переменной  х.

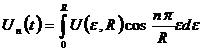        (n = 0, 1, 2, …)                          (9)

где  Un(t) – изображение U (x, τ) по переменной х [4]. Оригинал находится по формуле:

                                       (10)

Применяя это преобразование к уравнению (1) и условиям (2) при заданной  f (x) получим:

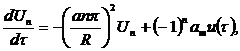                                                 (11)

                                                             (12)

       (n = 0, 1, 2, …)                                      (13)

Анализируя выражение (10), можно заключить, что уравнения (11) описывают процесс изменения коэффициентов Un ряда Фурье (10), являющегося решением уравнения (1). При этом начальными условиями служат выражения (12), т.е. коэффициенты разложения в ряд Фурье функции φ (х) начального условия (2). Желаемое конечное состояние задается аналогичной формулой (13) для функции f (х).

В результате оказалась сформулированной задача оптимального быстродействия для бесконечной системы обыкновенных дифференциальных уравнений (11) при ограничении на управляющие воздействия типа:

В дальнейшем будем рассматривать задачу оптимального быстродействия для конечного числа (m + 1) уравнений (11). При этом очень важно получить оценку погрешности, возникающую вследствие этого. Используя известное свойство рядов Фурье [5] и с учетом (10) и (13), получим:

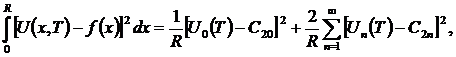              (14)

С другой стороны общее решение уравнений (11) имеет вид:

.

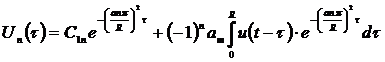Далее, используя ограничение (8), найдем:

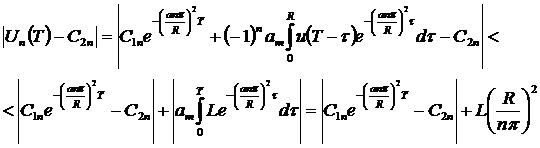
Воспользовавшись этим неравенством и выражением (14) получим искомую оценку:

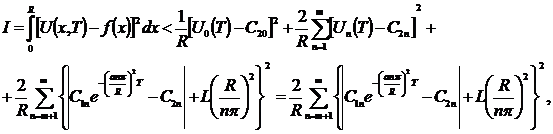      (15)

Так как в момент времени τ = Т имеем

            (n = 0, 1, 2, …, m)

В самом простом, но важном для практического применения случае, когда:

    

С1n = 0,  C2n = 0  при  n > 0, как это следует из (12), (13) оценка (15) приобретает вид:

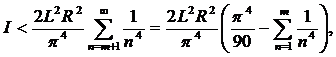                                               (16)

так как [5]

                                                         .

Отсюда следует, что правая часть неравенства (16) может стать сколь угодно малой, если  m  достаточно велико.

Таким образом, можно рассматривать задачу оптимального по быстродействию перемещения из точки С1 = (С10, С11, …, С1m) в точку С2 = (С20, С21, …, С2m) для  (m + 1) первых уравнений (11) при  фиксированном  m.

Рецензенты:

Черемных Н.Н., д.т.н., профессор, заведующий кафедрой Начертательной геометрии и машиностроительного черчения «Уральский государственный лесотехнический университет», г.Екатеринбург;

Уласовец В.Г., д.т.н., профессор кафедры механической обработки древесины ФГБОУ ВПО « Уральский государственный лесотехнический университет», г.Екатеринбург.