Изучение динамики незамкнутых кинематических цепей с конечным числом степеней свободы является актуальной задачей для различных областей науки и техники, например, исследование динамики механических манипуляторов [5]. Одним из распространенных методов формирования математической модели движения таких систем является метод уравнений Лагранжа второго рода [2, 4, 6], для составления которых необходимо выражение для кинетической энергии системы в обобщенных координатах. Поэтому формирование общего выражения для кинетической энергии системы с конечным числом степеней свободы является актуальной задачей.
Цель исследования.
Целью данной работы является получение общего выражения для кинетической энергии механической системы шарнирно-соединенных стержней с конечным числом степеней свободы, схема которой представлена на рис. 1.
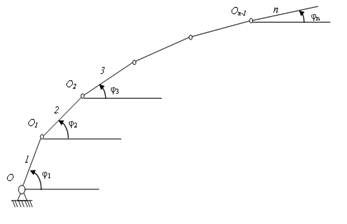
Рис. 1 – Кинематическая схема
1, 2, 3, … , n – абсолютно-твердые стержни; О, O1, O2, … , On-1 – идеальные шарниры;
φ1, φ2, φ3, … , φn – углы поворота стержней
Материалы и методы.
Рассматривается механическая система, состоящая из n абсолютно-твердых стержней, длины которых обозначим li. Стрежни соединены между собой шарнирами Oi. Стержень 1 закреплен при помощи неподвижного цилиндрического шарнира O.
Система имеет n степеней свободы. В качестве обобщенных координат выбраны углы поворота стержней φi. Таким образом, уравнения Лагранжа II рода можно записать в виде
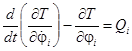 , (1)
, (1)
где φi – обобщенные координаты системы, ![]() – обобщенные скорости,
– обобщенные скорости, ![]() – обобщенные силы, T – кинетическая энергия системы.
– обобщенные силы, T – кинетическая энергия системы.
Кинетическая энергия системы определяется как сумма кинетических энергий n стержней по формуле
![]() , (2)
, (2)
где Ti – кинетическая энергия i-го стержня.
В работе [6] получены выражения для кинетических энергий стержня 1 и стержня 2:
![]() ; (3)
; (3)
![]() , (4)
, (4)
где m1 и m2 – массы стержней 1 и 2 соответственно.
Кинетическая энергия произвольного i-го стержня (для i > 2) может быть определена по формуле [2, 4, 6]
![]() , (5)
, (5)
где ![]() – масса k-ой точки i-го стержня,
– масса k-ой точки i-го стержня, ![]() – вектор скорости k-ой точки i-го стержня.
– вектор скорости k-ой точки i-го стержня.
Скорость ![]() (рис. 2) определяется теоремой сложения скоростей [2]
(рис. 2) определяется теоремой сложения скоростей [2]
![]() , (6)
, (6)
где ![]() – вектор скорости шарнира О1,
– вектор скорости шарнира О1, ![]() – вектор относительной скорости шарнира О2,
– вектор относительной скорости шарнира О2, ![]() - вектор относительной скорости шарнира Оi-1,
- вектор относительной скорости шарнира Оi-1, ![]() – вектор относительной скорости k-ой точки i-го стержня.
– вектор относительной скорости k-ой точки i-го стержня.
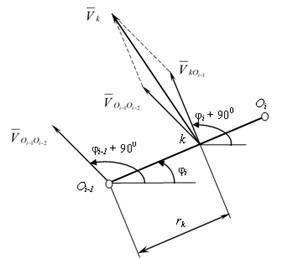
Рис. 2 – Схема к определению вектора скорости
Запишем выражение для квадрата скорости
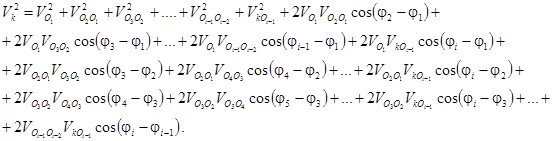 (7)
(7)
Представим выражение (7) в виде
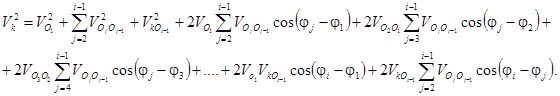 (8)
(8)
Выразим скорость шарнира O1 и относительные скорости через угловые скорости и длины стержней
![]() ,
, ![]() ,
,
![]() , … ,
, … , ![]() ,
,
![]() ,
,
где rk – расстояние от k-ой точки i-го стержня до полюса Oi-1.
Подставляя выражения для скоростей в выражение (7) получим
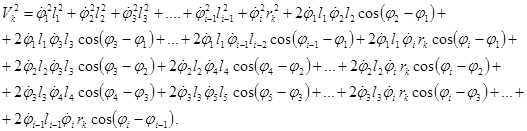 (9)
(9)
С учетом зависимости (8) выражение (9) может быть записано в сокращенном виде
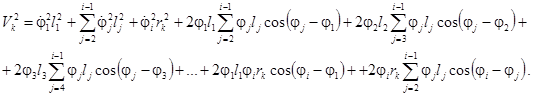 (10)
(10)
Подставляя (10) в выражение (5), получим выражение для кинетической энергии i-го стержня
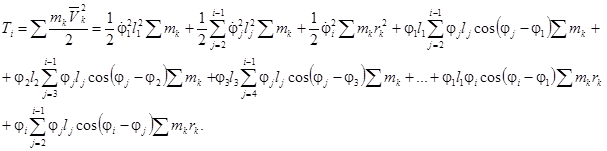 (11)
(11)
В данном выражении: ![]() – масса i-го стержня,
– масса i-го стержня, ![]() – статический момент i-го стержня относительно точки Oi-1,
– статический момент i-го стержня относительно точки Oi-1, ![]() – момент инерции i-го стержня относительно точки Oi-1. Тогда для кинетической энергии i-го стержня получим
– момент инерции i-го стержня относительно точки Oi-1. Тогда для кинетической энергии i-го стержня получим
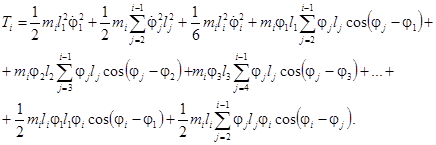 (12)
(12)
С учетом выражений (2), (3) и (4), кинетическую энергию всей системы представим в виде
![]() ,
,
где Ti определяется по формуле (12).
Приведем выражение для кинетической энергии системы к виду удобному для упрощения расчетов и возможности их автоматизации
![]() . (13)
. (13)
Слагаемое A1 определяется выражением:
![]() ,
,
где a1m – коэффициенты, характеризующие инерционные свойства системы, определяемые по формулам:
![]() ,
, ![]() , …. ,
, …. , ![]() , … ,
, … , ![]() .
.
Слагаемое A2 определяется выражением:
![]() ,
,
где a2m – коэффициенты, определяемые по формулам:
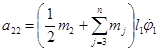 ,
, 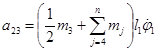 , …. ,
, …. ,
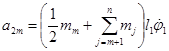 , … ,
, … , ![]() .
.
Слагаемое A3 определяется выражением:
![]() ,
,
где a3m – коэффициенты, определяемые по формулам:
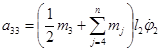 ,
, 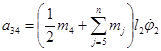 , …. ,
, …. ,
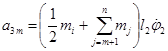 , … ,
, … , ![]() .
.
Произвольное слагаемое Ai (для 2 < i < n) определяется выражением
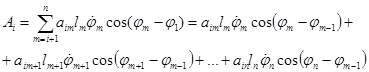 ,
,
где aim – коэффициенты, определяемые по формулам:
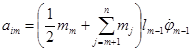 ,
, ![]() .
.
Слагаемое An определяется выражением:
![]() .
.
Результаты и их анализ.
Рассмотрим случай, когда все стержни имеют одинаковые длины (li = l) и массы (mi.=.m). Тогда полученные выражения для Ai упрощаются.
Слагаемое A1 определяется выражением:
![]() ,
,
где a1m – коэффициенты, характеризующие инерционные свойства системы, определяемые по формулам:
![]() ,
, ![]() , …. ,
, …. , ![]() , … ,
, … , ![]() .
.
Слагаемое A2 определяется выражением:
![]() ,
,
где a2m – коэффициенты, определяемые по формулам:
![]() ,
, ![]() , …. ,
, …. ,![]() , … ,
, … , ![]() .
.
Слагаемое A3 определяется выражением:
![]() ,
,
где a3m – коэффициенты, определяемые по формулам:
![]() ,
, ![]() , …. ,
, …. , ![]() , … ,
, … , ![]() .
.
Произвольное слагаемое Ai (для 2 < i < n) определяется выражением
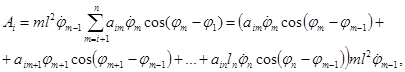
где aim – коэффициенты, определяемые по формулам:
![]() ,
, ![]() .
.
Слагаемое An определяется выражением:
![]() .
.
Заключение.
Полученное выражение (13) может быть использовано для определения кинетической энергии механической системы шарнирно-соединенных стержней с конечным числом степеней свободы, для составления дифференциальных уравнений и исследования движения таких систем, а также для разработки методов автоматизации расчетов для задач данного класса.
Рецензенты:
Панов А.Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород;
Иванов А.А., д.т.н., профессор кафедры «Автоматизации машиностроения», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Библиографическая ссылка
Смирнов Д.А. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ ШАРНИРНЫХ СТЕРЖНЕЙ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16593 (дата обращения: 12.03.2026).



