Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Волков Ю.Д. 1

---

1 Мордовский государственный университет им. Н.П. Огарева

Рассмотрена задача оптимизации эксперимента в условиях неопределенности на примере технических систем. Представлены два подхода к определению неопределенности, вероятностный и нечеткий. Дан анализ моделей эксперимента. На ранних этапах эксперимента целесообразно использовать нечеткую модель активного эксперимента в пространстве состояний. Проведена фаззификация задачи эксперимента с использованием нечетких FN-чисел. Для математической модели обработки неопределенности, появляющейся при измерении (оценке) параметров, предлагается арифметика FN-чисел. Введен показатель энергетической цены, который учитывает полную мощность экспериментальной установки и временные затраты на проведение эксперимента в оценочной функции общего вида. Процедура поиска с использованием оценочной функции обладает свойствами алгоритма Харта, Нильсона и Рафаэля, что дает реальный выигрыш в объеме перебора. В результате снижаются энергозатраты и осуществляется контроль за точностью обработки данных на всех этапах эксперимента.

Статья в формате PDF

281 KB

задача эксперимента

неопределенность

нечеткая модель

оптимизация по энергозатратам

1. Волков Ю.Д., Кочугаев П.Н. Модели эксперимента в условиях неопределенности. «Науч.-техн. вестник Поволжья», №6, 2013, с.215-218.

2. Волков Ю.Д., Кочугаев П.Н. Нечеткие вычисления при моделировании эксперимента // Информационно-вычислительные технологии и их приложения: сб. статей XIV Межд. науч.-техн. конф. (Пенза, 11-13 дек. 2010 г.).-Пенза, РИО ПГСХА, 2010. С.64-68.

3. Волков Ю.Д.. Интеллектуализация эксперимента в технических системах// Региональная информатика (РИ-2014): материалы XIV межд. конф. (Санкт-Петербург, 29-31 окт. 2014 г.).- СПОИСУ,-СПб. 2014. С.24-25.

4. 2. Волков Ю.Д., Дудин А.В. Оптимизация эксперимента по энергозатратам в условиях вероятностной неопределенности. «Науч.-техн. вестник Поволжья», №5, 2014, с.147-149.

5. Guide to the Expression of Uncertainty in Measurement: First Edition. – ISO, Switzerland, 1993. – 101 р.

6. Hart P.E., Nilsson N.J., Raphael B. Correction to “A Formal Basis for the Heuristic Determination of Minimum Cost Paths” //SIGART Newsletter. -1972.-T.37.-C.28-29.

При проведении эксперимента в технических системах на ранних стадиях одной из проблем является целенаправленное управление в условиях неопределенности, связанной, в частности, с возможностями измерений и случайным характером процессов [1]. Растущие требования к точности результатов удовлетворяются не только за счет применения прецизионных приборов, но и путем использования методов мягких вычислений и измерений [1,2]. Неопределенность измерения состоит из двух компонент, названных в [5] неопределенностью категории А и В. Если к А относят объективные вероятностные оценки ряда измерений, то при поиске компонентов категории В возможно использование субъективных знаний, формализованных с применением теории нечетких множеств [1,3].

Алгоритм управления экспериментом должен обеспечивать наиболее выгодный компромисс между качеством решения и стоимостной эффективностью со следующими ограничениями:  где  - время и энергозатраты  -эксперимента. Для заполнения пробела в области структуризованной неопределенности там, где нельзя корректно применять статистические методы, можно использовать теорию нечетких множеств, либо комбинировать нечеткость и вероятность. Рассмотрим модели, построенные в рамках этих подходов. Сформулируем критерии оптимизации эксперимента, необходимые для решения задачи активного эксперимента. Предварительно напомним некоторые результаты, полученные в [1-4], а также уточним исходные понятия.

Вероятностная модель эксперимента

Эксперимент интерпретируется как процесс поиска решения проблемы. Возможно, что нам априори известны вероятности гипотез  из ранее набранной статистики.

Задача 1. Пусть относительно объекта исследований выдвинута полная группа из -попарно несовместных гипотез с вероятностями , причем 

                                                                (1)

Имеется множество допустимых экспериментов Q по верификации этих гипотез и соответствующие стоимости их проведения C. Требуется оптимизировать процесс экспериментального подтверждения одной из гипотез .

Знание  позволяет произвести целенаправленный эксперимент и соответственно уменьшить его стоимость C. Верификацию гипотез  можно вести согласно вероятностной модели активного эксперимента [1, 3] , которая имеет вид

,                                                      (2)

где – вероятностное пространство с  и вероятностной мерой .

Проведение эксперимента связано с подачей управляющих воздействий  на экспериментальную установку, измерением параметров  и результатом первичной обработки информации . Эта совокупность "атомарных" действий конечная, будем считать ее элементарным экспериментом и обозначим . Последовательное выполнение экспериментов  интерпретируется как композиция  отображений . Таким образом, получена алгебраическая система  со свойствами замкнутости, ассоциативности, идемпотентности, необратимости. Система  действует в  с соответствующей . Выбор возможной последовательности будем оценивать функцией качества  [1].

В рамках модели (2) сформулируем оптимизационную задачу эксперимента

,                            (3)

где "*"- символ операции мультипликативной, либо аддитивной функции .

Для реализации вероятностной модели эксперимента необходимо знание исходного распределения вероятностей . При отсутствии такой оценки на ранних стадиях эксперимента применим лингво-численную оценку с помощью высказываний, например: вероятность гипотезы составляет «около или близко к 0,5».

Фаззификация задачи эксперимента

Ослабим условия задачи 1 и вместо точечной оценки  введем эмпирическую или теоретическую оценку степени принадлежности вероятности -гипотезы , где  - множество выпуклых функций принадлежности.

Задача 2. Пусть относительно объекта исследований выдвинута группа из - гипотез  с оценками их вероятностей имеющимися функциями принадлежности . Имеется множество экспериментов  по верификации гипотез и энергозатраты на их проведение . Требуется оптимизировать процесс подтверждения одной из гипотез .

В этом случае условие несовместности гипотез и ограничение (1) может не выполняться.

Отразим исходную неопределенность значений измеряемой величины нечеткими числами  с функциями принадлежности  в LR-формате, который выбирается из условия минимума отклонения от гауссовской функции [2,3]. На ранних стадиях эксперимента предлагается использовать унимодальные нечеткие-числа, так как они более адекватно оценивают высказывания типа «вероятность  приблизительно равна 0,5», рис.1.

Рисунок 1 - Переход от нормального закона к унимодальному LR-формату

Аналитически  записывается следующим образом:

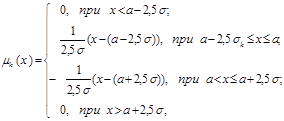                                                    (4)

- усредненная оценка значений измеряемой величины, данная через n- измерений или оценок экспертов; - соответствующее среднеквадратичное отклонение оценки.

Для математической модели обработки неопределенности, появляющейся при измерении параметров, предлагается арифметика нечетких чисел.

Арифметика нечетких FN-чисел

Пусть - усредненная оценка значений измеряемой величины, - среднеквадратичное отклонение оценки. Определим нечеткое число в виде пары , где - ширина интервала нечеткого числа.

Определение 1. Нечеткие числа, функция принадлежности которых имеет график в форме равнобедренного треугольника (трапеции), будем называть нечеткими естественными () числами и записывать в виде .

При этом операции сложения и умножения введены по следующим правилам.

Сложение.    : .                                      (5)

Умножение. : ,.             (6)

Замечание. Операция сложения полностью совпадает с обычной операцией для нечетких чисел, операция умножения применяется с округлением. Указанные операции упрощают действия над нечеткими числами и согласуются с арифметикой погрешностей измерений.

Как известно, операции  выражаются через операции  посредством симметрии и инверсии соответственно. Имеет место следующее утверждение.

Утверждение. Операции сложения  и умножения  на множестве FN-чисел определяют структуру коммутативного кольца.

Доказательство утверждения – прямые вычисления.

Определение 2. Нечетким множеством оценок назовем

.                                  (7)

На множестве  получена -арифметика нечетких чисел , которая позволяет оперировать с FN-числами в рамках поставленной задачи.

Таким образом, мы можем перейти от «лингво-численной» к нечеткой оценке исходного распределения вероятностей гипотез , рис.2.

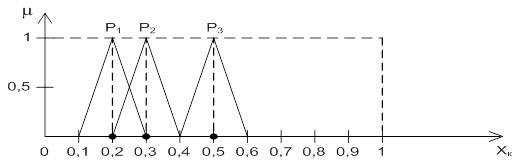
Рисунок 2 - Оценка вероятностей гипотез «около 0,2; около 0,3; около 0,5» FN-числами

Нечеткая модель эксперимента

Пусть  дискретное пространство состояний, в котором определено начальное состояние  , что отражает исходную неопределенность в виде полной группы гипотез  и , как возможное поле действия эксперимента. Промежуточному состоянию  поставим в соответствие вершину –мерного куба  и грань булева куба, то есть набор  при отбрасывании гипотезы,  - в противном. Ввиду неопределенности элементарный эксперимент свяжем с отображением нечетких множеств

,                        (8)

которому соответствует нечеткий оператор .

В этом случае  определяет нечеткое отношение  на , которое обладает важным свойством: пространство  включает в себя промежуточные подпространства, вплоть до конечных  . Отношение  можно отнести к нечетким порядковым отношениям, так как не имеет контуров, обладает свойствами антисимметричности, транзитивности и антирефлексивности.

Антисимметричность.         

. Нечеткий оператор  отображает пространство S в себя и преобразование направлено в сторону уменьшения энтропии эксперимента Н. Источником ошибок могут быть помехи, погрешности и неправильные действия при проведении эксперимента. Антисимметричные отношения задают на  отношения упорядоченности, доминирования, подчинености. Отношению  можно поставить в соответствие один (и только один) взвешенный антисимметричный граф  с матрицей отношений, в котором каждая пара вершин  соeдиняется стрелкой с весом , рис.3.

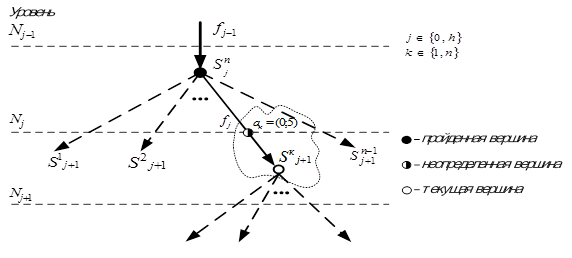
Рисунок 3 - Поиск в пространстве S при нечетком подходе

Элементами нечеткой модели эксперимента являются

,                                               (9)

где  - алгебраическая система с одной определяющей операцией ; - дискретное пространство  с отношением , арифметикой -чисел  и функций .

Оптимизация эксперимента по энергозатратам

Будем учитывать особенности процесса эксперимента при нечетком представлении. В отличие от вероятностного подхода задача (2) сводится к поиску оптимального (сильнейшего) пути  из  в одно из  на графе эксперимента . Оптимальный путь определяется как .

Если в результате -эксперимента отвергнута гипотеза  (произошло событие ), то вследствие теоремы Байеса получаем апостериорные оценки вероятностей гипотез

 при условии .                                                (10)

Неопределенность, возникающую в процессе эксперимента, введем появлением в последовательности координатой  - «состояние не определено, не знаю». На практике это означает проведение дополнительного, уточняющего эксперимента, рис.3.

После проведения  определяются количественные значения  и направление поиска. Так как решение задач активного эксперимента в технических системах неразрывно связано с преобразованием и передачей энергии при проведении эксперимента, стоимостную эффективность эксперимента будем характеризовать таким показателем как энергетическая цена , которая учитывает полную мощность экспериментальной установки  и временные затраты на -м этапе эксперимента 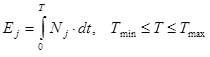. В общем, за оценку энергозатрат принимаем математическое ожидание потерь, которое представляет собой сумму ожидаемых затрат по всем -путям от корня графа  к каждой из конечных вершин , умноженных на оценку

                                    (11)

Разложим оценку энергозатрат для -ой вершины графа на составляющие

,                                             (12)

где  - энергозатраты на реализацию последовательности экспериментов  от вершины  до вершины ; - математическое ожидание, а  - дисперсия оценки будущих затрат на реализацию пути от  до одного из . Функция  монотонна, так как из  следует . Процедура поиска с оценочной функцией (12) обладает свойствами алгоритма Харта, Нильсона и Рафаэля [6], причем объем перебора при поиске не более, чем в известных методах.

Для оптимизации в процессе эксперимента воспользуемся рекуррентной формулой, которая получается из (12), если выделим слагаемое, содержащее первый ,

                                (13)

Согласно (13) оценка энергозатрат  сводится к суммированию взвешенной энергетической цены  с оценкой будущих энергозатрат программы эксперимента. При этом необходим пересчет оценок по формуле (10) при опровержении -гипотезы.

Фактически  дает оценку стоимости наиболее выгодного пути, связывающего начальную вершину  с  и проходящего через вершину . В этом случае  можно не учитывать, так как , где. - действительные энергозатраты.

Пример. Имеется оценка вероятностей трех гипотез в виде , подмножество экспериментов по верификации этих гипотез  и соответственно энергозатраты на их проведение . Вначале . Затем, пересчитывая по формулам (5,6), (10-13), получим следующие значения оценок энергозатрат после проведения экспериментов,

  , ;

 , ;

 . .

Для реализации выбираем эксперимент  и присваиваем . При равенстве значений  при выборе будем исходить из величины , характеризующей точность результата эксперимента.

Вывод. Оптимизация эксперимента по энергозатратам на  дает реальный выигрыш в объеме перебора по сравнению с тем же алгоритмом поиска, реализуемом без нечетких оценок. Также не требуется предварительное определение всех состояний , так как выбор совокупности экспериментов  идет от начального состояния  к . По ходу поиска определяются только те состояния, которые получаются при реализации на данном этапе выбранного эксперимента, благодаря чему сокращается объем вычислений. За возможность оперировать с нечеткими оценками приходится платить громоздкостью вычислений и ростом интервала , что в полной мере отражает реальность и, в сущности, соответствует принципу возрастания неопределенности (энтропии) эксперимента. В результате мы можем следить за точностью всех этапов эксперимента, включая обработку информации и определять необходимый уровень точности.

Рецензенты:

Чаткин М.Н., д.т.н., профессор, ректор ФГБОУ «Мордовский институт переподготовки кадров агробизнеса», г.Саранск;

Щенников В.Н., д ф-м. н., профессор ФГБОУ ВПО «МГУ им. Н.П. Огарева, г. Саранск.

Библиографическая ссылка