Рассмотрим роботизированную платформу, предназначенную для защиты технологических объектов, а также человека-оператора от низкочастотных воздействий со стороны основания. При этом поставим обратную робототехническую задачу: при любых случайных воздействиях со стороны подвижного основания построить такой закон управления приводным механизмом, при котором объект (платформа) является неподвижным в инерциальной системе координат. При этом необходимо рассмотреть вопросы выбора схем и конструкций приводов и типа датчиков, а также синтеза системы управления.
В качестве привода будем рассматривать электромеханический исполнительный механизм (рис.1), который является наиболее простым по своему конструктивному исполнению и эксплуатационным характеристикам.[1] Кроме того, он обеспечивает большие относительные перемещения, порядка десятка сантиметров и возможность эксплуатации в неблагоприятных средах. Частотный диапазон работы определяется, главным образом, частотным диапазоном используемого электродвигателя. В качестве датчиков обратных связей используем акселерометры, установленные на объекте и основании, и датчик относительного перемещения.[2]
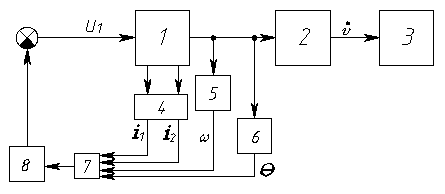
Рис. 1. Система с электромеханическим исполнительным механизмом с шарико-винтовой парой: 1 — электродвигатель; 2 — шарико-винтовая пара; 3 — объект виброзащиты; 4 — датчик тока; 5 — датчик скорости; 6 — датчик положения; 7 — регулятор;
8 — усилитель мощности.
Построим математическую модель привода. В винтовой шариковой паре модель передачи скоростей и момента описывается уравнениями:
![]() ; (1)
; (1)
где ![]() - шаг резьбы,
- шаг резьбы, ![]() - число заходов резьбы,
- число заходов резьбы, ![]() - скорость вращения якоря двигателя,
- скорость вращения якоря двигателя, ![]() - перемещение основания[3]
- перемещение основания[3]
Рассмотрим двухфазный шаговый электродвигатель с активным неявнополюсным ротором. Примем за начало отсчета угла ![]() положение, при котором ось полюса ротора совпадает с осью фазы 1. При этом
положение, при котором ось полюса ротора совпадает с осью фазы 1. При этом
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Запишем уравнения напряжений и момента
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() ; (4)
; (4)
![]() ; (5)
; (5)
где ![]() - момент нагрузки,
- момент нагрузки, ![]() - момент инерции ротора двигателя,
- момент инерции ротора двигателя, ![]() - ток, сопротивление и напряжение 1-й фазы двигателя,
- ток, сопротивление и напряжение 1-й фазы двигателя, ![]() - ток, сопротивление и напряжение 2-й фазы двигателя,
- ток, сопротивление и напряжение 2-й фазы двигателя, ![]() - угол между осью полюсов и вектором н. с.,
- угол между осью полюсов и вектором н. с., ![]() - число пар полюсов,
- число пар полюсов, ![]() - максимальное потокосцепление возбужденного ротора с одной фазой статора,
- максимальное потокосцепление возбужденного ротора с одной фазой статора, ![]() - коэффициент взаимоиндукции,
- коэффициент взаимоиндукции, ![]() - угловая скорость
- угловая скорость
![]() Из уравнений 1- 5 получена система уравнений
Из уравнений 1- 5 получена система уравнений
![]() ,
,
![]() ,
,
![]() , (6)
, (6)
![]() ,
,
Упростим уравнения (6), приняв угол ![]() близким к нулю (при этом
близким к нулю (при этом ![]() , а
, а ![]() ), а затем приведем их к виду, характерному для уравнений, описывающих систему в пространстве состояний, приняв
), а затем приведем их к виду, характерному для уравнений, описывающих систему в пространстве состояний, приняв
![]()
![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() , (7)
, (7)
![]() .
.
![]() Введем 4 переменные состояния:
Введем 4 переменные состояния: ![]() ,
, ![]() ,
, ![]() и
и ![]() . Система уравнений (7) примет вид
. Система уравнений (7) примет вид
![]() ,
,
![]() ,
,
![]() , (8)
, (8)
![]()
![]() .
.
или в векторно-матричной форме
![]()
![]() ;
;
(9)
![]() ,
,
где ![]() - вектор состояния,
- вектор состояния, ![]() - вектор возмущающего воздействия,
- вектор возмущающего воздействия, 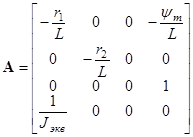 и
и 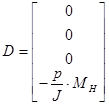 - матрицы коэффициентов системы,
- матрицы коэффициентов системы, ![]() - вектор входных сигналов,
- вектор входных сигналов, 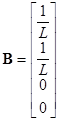 - коэффициент входных сигналов,
- коэффициент входных сигналов, ![]() - вектор-строка входных сигналов.
- вектор-строка входных сигналов.
Исследование динамических свойств исполнительного механизма при дискретном входном сигнале
![]() Работа шагового двигателя осуществляется в результате подачи на вход импульсов напряжения. В связи с этим переведём первое уравнение системы уравнений 9 в дискретную форму. В результате получим
Работа шагового двигателя осуществляется в результате подачи на вход импульсов напряжения. В связи с этим переведём первое уравнение системы уравнений 9 в дискретную форму. В результате получим
![]() ;
;
(12)
![]() ,
,
где ![]() ;
; 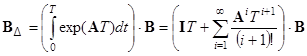 ;
;
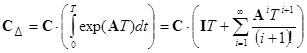 (13)
(13)
В матричном уравнении (12) символы ![]() ,
, ![]() ,
, ![]() и
и ![]() обозначают аналоги матриц
обозначают аналоги матриц ![]() ,
, ![]() , C и D для дискретной системы, а символ
, C и D для дискретной системы, а символ ![]() введён для обозначения периода дискретизации. Ввиду большой сложности математических выкладок представляется нецелесообразным выводить общий вид матриц
введён для обозначения периода дискретизации. Ввиду большой сложности математических выкладок представляется нецелесообразным выводить общий вид матриц ![]() ,
, ![]() ,
, ![]() и
и ![]() . Удобнее рассчитывать матрицы
. Удобнее рассчитывать матрицы ![]() ,
, ![]() ,
, ![]() и
и ![]() в числовом виде для каждой конкретной четверки матриц
в числовом виде для каждой конкретной четверки матриц ![]() ,
, ![]() , C и D.
, C и D.
Перейдём к передаточной функции, описывающей влияние напряжений на якоре ![]() на скорость поступательного движения механизма
на скорость поступательного движения механизма ![]()
![]() (14)
(14)
где ![]() - переходная матрица состояния.
- переходная матрица состояния.
Из уравнения (14) может быть выражена передаточная функция, описывающая влияние напряжений на якоре ![]() на угловую скорость вращения вала двигателя
на угловую скорость вращения вала двигателя ![]()
![]() (15)
(15)
Исходя из требований, предъявляемых к системе, и рекомендаций по расчёту винтовой шариковой передачи, составим таблицу исходных технических данных для расчёта винтовой шариковой передачи (табл.1).
В качестве примера рассмотрим шаговый электродвигатель FL20STH, имеющий следующие технические характеристики (табл. 2).
Таблица 1
Исходные технические данные для расчета винтовой шариковой передачи
|
№ п/п |
Наименование характеристики и обозначение |
Единица измерения |
Значение |
|
1. |
Шаг резьбы |
— |
2 |
|
2. |
Число заходов резьбы, n |
— |
5 |
Таблица 2
Технические данные шагового двигателя FL20STH
|
№ п/п |
Наименование характеристики и обозначение |
Единица измерения |
Значение |
|
1. |
Мощность электродвигателя номинальная, P |
Вт |
|
|
2. |
Напряжение якоря номинальное, Uном |
В |
|
|
3. |
Момент нагрузки, Мном |
кг×м |
18·10-4 |
|
4. |
Момент инерции ротора, J |
кг×м2 |
9·10-7 |
|
5. |
Число пар полюсов, p |
|
4 |
|
6. |
Максимальное потокосцепление возбужденного ротора с одной фазой статора, ψm |
|
5·10-4 |
|
7. |
Сопротивление фазы двигателя, r1, r2 |
Ом |
5,6 |
|
8. |
Индуктивность якоря, L |
Гн |
0,42 |
После проведения соответствующих вычислений получаем передаточную функцию
![]() (16)
(16)
Для нашей системы (12) найдем управление
![]() (17)
(17)
которое минимизирует[4]
![]() (18)
(18)
Введем во второе уравнение системы (12) управление u. Сделано это для ограничения величины используемого управления, т.к. в противном случае можно добиться сколь угодно маленького значения J с помощью достаточно больших u. Система (12) примет вид
![]()
![]() ;
;
(19)
![]() ,
,
Как известно
![]() , (20)
, (20)
где ![]() – передаточная функция замкнутой системы от возмущения ω к выходу y, т.е. минимизация J эквивалентна задаче H∞-оптимизации.[5]
– передаточная функция замкнутой системы от возмущения ω к выходу y, т.е. минимизация J эквивалентна задаче H∞-оптимизации.[5]
Преобразуем предварительно ![]()
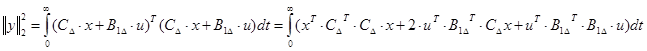 (21)
(21)
Предположим для простоты выкладок, что ![]() , тогда смешанное произведение отсутствует
, тогда смешанное произведение отсутствует
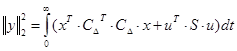 (22)
(22)
где
![]() (23)
(23)
Таким образом задача записывается так
![]() ,
, ![]() ,
, ![]() ,
, ![]() (24)
(24)
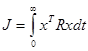 , где
, где ![]() (25)
(25)
Если неравенство
![]() (26)
(26)
имеет решение P>0, то J≤γ2.
Умножим неравенство (20) слева и справа на Q=P-1
![]() (27)
(27)
и сделаем замену ![]()
![]() (28)
(28)
Преобразуем члены, зависящие от Y
![]() (29)
(29)
причем равенство достигается при ![]() .
.
Неравенство (23) выполняется при некоторых Q>0, Y тогда и только тогда, когда выполняется неравенство относительно Q>0
![]() (30)
(30)
В свою очередь он имеет положительно-определенное решение Q>0, если такое решение имеет уравнение Рикатти, полученное заменой неравенства на равенство. По этому решению восстанавливаем соответствующий стабилизирующий регулятор
![]() (31)
(31)
Матрицы ![]() ,
, ![]() и D уравнения (12) для такой системы будут следующими:
и D уравнения (12) для такой системы будут следующими:
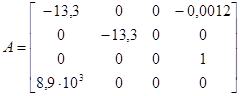 ,
, 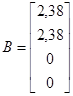 ,
, ![]()
Перейдя к дискретной задаче, приняв период дискретизации ![]() с, получим следующие матрицы
с, получим следующие матрицы ![]() ,
, ![]() ,
, ![]() уравнения (12):
уравнения (12):
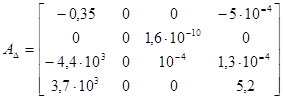 ,
,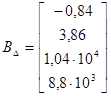 ,
,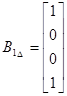 ,
,![]() ,
, 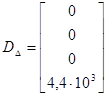
Установим следующие значения весовых коэффициентов:
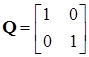 ,
, ![]()
После выполнения процедуры нахождения коэффициентов обратных связей оптимального регулятора была получена матрица коэффициентов обратных связей
K = [0,0984; 0; 0,0001; 0,0001]
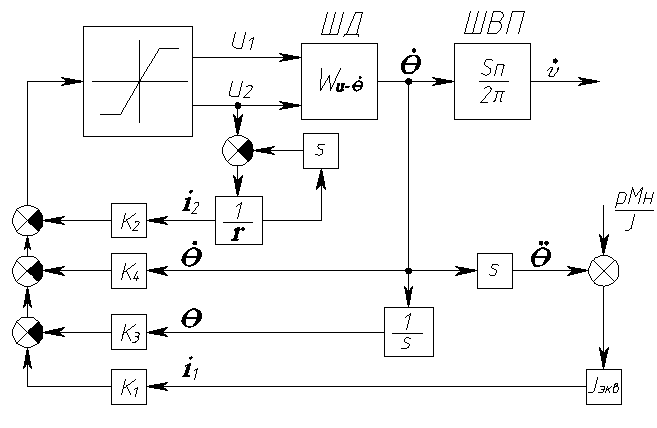
Рис. 2. Структурная схема системы виброзащиты с электромеханическим исполнительным механизмом: ШД – шаговый двигатель, ШВП – шарико-винтовая передача.
Выводы
Перспективным будет применение шагового двигателя. Позиционирование шаговым двигателем выполняется без проскальзывания и перерегулирования, также отсутствует зона нечувствительности. Отметим, что выбор или разработка электродвигателя для применения в подобных система требует специального исследования и поиска оптимальных решений с учётом развития техники.
Исследования реакции на внешнее возмущение показали высокую эффективность выбранной схемы электромеханического привода и алгоритма управления, а также пути дальнейших исследований и усовершенствований системы.
Рецензены:
Погонин А.А., д.т.н., профессор кафедры технологии машиностроения ФГБОУ ВПО Белгородского государственного технологического университета, г. Белгород;
Пелипенко Н.А., д.т.н., профессор Белгородского государственного национального исследовательского университета, г. Белгород.
Библиографическая ссылка
Черкашин Н.Н., Гапоненко Е.В., Мамаев Ю.А., Малышев Д.И. СИНТЕЗ ЦИФРОВОГО РЕГУЛЯТОРА РОБОТИЗИРОВАННОЙ ПЛАТФОРМЫ НА ОСНОВЕ H∞-ОПТИМИЗАЦИИ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16586 (дата обращения: 19.02.2026).



