Одним из методов временной селекции, основанном на использовании сигналов с высокой сложностью, является метод спектрометрии временных задержек [3, 5]. Принцип данного метода заключается в том, что излучается длительный широкополосный сигнал (линейно-частотно-модулированный сигнал). Принятый сигнал подвергается обработке с помощью процедуры согласованной фильтрации – гетеродинированию принятого сигнала опорным и эподавлению сигнала суммарной частоты с помощью фильтра нижних частот. В результате получается сигнал разностной частоты (РЧ).
Спектр сигнала РЧ представляет собой свертку суммы импульсных характеристик всех путей распространения звука с импульсной функцией зондирующего сигнала. Спектр сигнала РЧ также называют энерго-временной зависимостью (ЭВЗ) [4]. На рисунке изображен типичный для гидроакустики вид спектра сигнала РЧ (ЭВЗ). Каждому из лучей на рисунке соответствует свой пик («приход»). Временная селекция означает, что для анализа импульсной характеристики отдельного канала используется только N точек из соответствующего «прихода», как это показано пунктирными линиями.
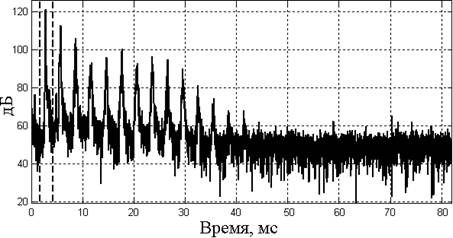
Рис. 1. Энергетический спектр сигнала разностной частоты
С точки зрения точности, оптимальным методом определения положения «прихода» является поиск максимума функции корреляции реального и т.н. идеального (образца) «прихода». Однако данный подход трудно реализовать из-за отсутствия такого образца в большинстве случаев. Более удобен метод оценки положения «прихода» по положению максимума. Точность оценки, в этом случае, зависит от остроты пика ЭВЗ, а под воздействием нелинейной АФЧХ тракта пик расширяется. Кроме того, для уменьшения взаимного влияния соседних «приходов» обычно применяются различные весовые окна (Хеннинга, Хемминга, Кайзера и т.д.). Наложение окон приводит к тому, что вершина «прихода» становится менее острой, из-за чего точность оценки положения «прихода» на основании положения его максимума снижается. В этом случае может оказаться более точным метод «вилочного» отсчёта [2].
В методе СВЗ по положению спектральных пиков ЭВЗ определяются задержки распространения. Используя метод «вилочного» отсчёта, нельзя найти абсолютную величину задержки распространения, однако можно с высокой точностью отслеживать относительные перемещения «приходов», или интервалы между несколькими «приходами», так как:
– форма спектральных пиков определяется амплитудно-частотными характеристиками тракта (главным образом резонансными характеристиками излучателя и приёмника) и со временем меняется очень слабо;
– при изменении задержки распространения изменяются только амплитуда «прихода» и его положение на оси задержек, без изменения формы, что не влияет на положение «вилочного» отсчёта относительно вершины «прихода».
Определение интервалов между пиками может оказаться также полезным в акустической тензометрии [1].
Влияние аддитивного шума на точность оценки частоты модулированного сигнала при дискретной обработке методом «вилочного» отсчёта
Обозначим ![]() ,
,
![]() , и
, и ![]()
функцию спектральной плотности сигнала
функцию спектральной плотности сигнала![]() .
.
![]() – гармонический сигнал, подвергшийся
частотной и фазовой модуляции:
– гармонический сигнал, подвергшийся
частотной и фазовой модуляции:![]() ,
,![]() ,а
,а ![]()
отсчёты его спектральной плотности.
отсчёты его спектральной плотности.
![]() реализация эргодического дельта коррелированного
случайного процесса
реализация эргодического дельта коррелированного
случайного процесса ![]() , с нулевым средним
значением и средним квадратическим отклонением
, с нулевым средним
значением и средним квадратическим отклонением ![]() .
.
![]() набор значений спектральной плотности,
случайного процесса
набор значений спектральной плотности,
случайного процесса ![]() , а
, а ![]() среднее квадратическое отклонение
спектральной плотности
среднее квадратическое отклонение
спектральной плотности ![]() :
:
![]() . (1)
. (1)
Требуется оценить влияние аддитивной
шумовой составляющей ![]() на точность оценки
положения «вилочного» отсчёта для спектрального максимума
на точность оценки
положения «вилочного» отсчёта для спектрального максимума ![]() .
.
Обозначим СКО положения «вилочного»
отсчёта, при воздействии аддитивного шума на пик, как ![]() . Можно показать,
что при больших соотношениях сигнал/шум (обычно отношение сигнал/шум при
СВЗ-измерениях составляет 60¸80 дБ):
. Можно показать,
что при больших соотношениях сигнал/шум (обычно отношение сигнал/шум при
СВЗ-измерениях составляет 60¸80 дБ):
![]() , (2)
, (2)
где 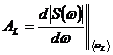 ,
,
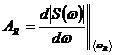 , а
, а ![]() и
и
![]() частоты, соответствующие положению
левой и правой границ «вилочного» отсчёта.
частоты, соответствующие положению
левой и правой границ «вилочного» отсчёта.
Таким образом СКО положения «вилочного»
отсчёта определяется соотношением мощности шума и величиной наклона модуля
спектра в крайних точках «вилочного» интервала. Очевидно, что максимальную
точность метод «вилочных» сможет обеспечить, если разность производных в точках
![]() и
и ![]() будет
максимально возможной. Поэтому предлагается подбирать ширину «вилочного»
интервала (
будет
максимально возможной. Поэтому предлагается подбирать ширину «вилочного»
интервала (![]() ) таким образом, чтобы величина
) таким образом, чтобы величина
![]() была максимальна.
была максимальна.
Постановка эксперимента и моделирование
В небольшом бассейне, при неизменных условиях, были произведены 40 измерений. По области спектра сигналов, в которой отсутствуют отражения, была получена мощность присутствующего в сигнале шума, на основании формулы (1).
Далее был проведён численный эксперимент. На гармонический сигнал накладывались различные временные окна (прямоугольное, Хеннинга, Кайзера). Затем к амплитудно-модулированному сигналу добавлялся шум той же мощности, что и в реальном сигнале с АЦП. Далее, методом нахождения максимума и методом «вилочных» отсчётов, вычислялось положение спектрального пика, искажённого шумом сигнала. СКО отклонений пика, для обоих методов, приводятся в таблице 1 (модельное значение СКО).
Таблица 1
Оценка СКО положения спектрального пика гармонического сигнала, в бинах
|
Весовое окно |
По положению максимума |
Методом «вилочных» отсчётов |
||
|
Теоретическое |
Модельное |
Теоретическое |
Модельное |
|
|
Прямоугольное |
0,000073 |
0,000075 |
0,000069 |
0,000078 |
|
Хеннинга |
0,000228 |
0,000233 |
0,000152 |
0,000164 |
|
Кайзера |
0,000649 |
0,000662 |
0,000310 |
0,000302 |
Теоретические значения СКО были получены:
– для метода нахождения максимума, на основании формулы:
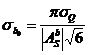 , где
, где 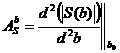 ,
а
,
а ![]() положение максимума в бинах (отсчётах
спектра);
положение максимума в бинах (отсчётах
спектра);
– для метода «вилочных» отсчётов на основании формулы (2).
Тот же эксперимент был проведён для одной реализации сигнала с акустического приёмника, полученной при СВЗ измерении, для оценки влияния формы «приходов» на точность методов (таблица 2, модельное значение СКО). Затем СКО для обоих методов были получены из результатов 40 реальных измерений (таблица 2, экспериментальное значение СКО).
Таблица 2
Оценка СКО положения спектрального пика сигнала разностной частоты, в бинах
|
Весовое Окно |
По положению максимума |
Методом «вилочных» отсчётов |
||||
|
Теорети-ческое |
Модель- ное |
Экспери-ментальное |
Теорети-ческое |
Модель- ное |
Экспери-ментальное |
|
|
Прямоугольное |
0,000376 |
0,000391 |
0,000369 |
0,000262 |
0,000266 |
0,000227 |
|
Хеннинга |
0,000479 |
0,000489 |
0,000488 |
0,000295 |
0,000285 |
0,000312 |
|
Кайзера |
0,000747 |
0,000750 |
0,000786 |
0,000334 |
0,000328 |
0,000333 |
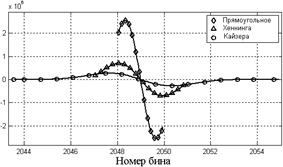
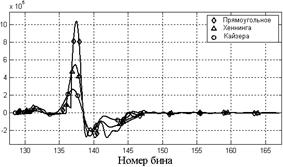
Рис. 2. Производные модулей спектров: а – гармонического сигнала, взвешенного различными весовыми окнами; б – сигнала с приёмника, взвешенного различными весовыми окнами
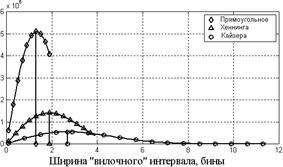
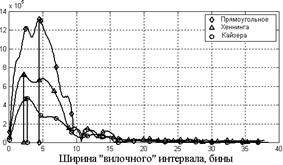
Рис. 3.Кривые относительной точности метода для: а – гармонического сигнала, взвешенного различными весовыми окнами; б – сигнала с приёмника, взвешенного различными весовыми окнами
Наложение окон Хеннинга и Кайзера приводит к расширению спектрального пика, в результате чего уменьшаются производные модуля спектрального пика (рисунок). На основании вычисленных значений |AL‑AR| для различных значений ширины «вилочного» интервала были построены кривые относительной точности (рисунок). Из кривых можно найти оптимальное значение ширины «вилочного» интервала, т.к. максимум функции |AL‑AR| соответствует максимальной точности метода «вилочных» отсчётов. Заметим, что данные в таблице 1 и таблице 2 приводятся только для оптимальных значений «вилочного» интервала.
Устойчивость метода к влиянию гармонической помехи
Для того чтобы оценить чувствительность метода «вилочного» отсчёта к наличию в спектре сигнала других спектральных пиков, был проведён численный эксперимент. К гармоническому сигналу известной частоты f1 («полезный» сигнал) добавлялся сигнал с частотой f1 («помеха»). Затем методом «вилочного» отсчёта и методом поиска максимума оценивалась частота полезного сигнала, присутствующего в аддитивной смеси. Были построены зависимостей величины ошибки от разности частот |f1‑f1|. Моделирование показало, что метод «вилочного» отсчёта более устойчив к влиянию аддитивной гармонической помехи, за исключением тех случаев, когда частота помехи близка к частоте «полезного» сигнала. Для гармонических сигналов, применение метода вилочных отсчётов целесообразно в тех случаях, когда расстояние между соседними спектральными максимумами составляет не менее: для прямоугольного окна 7 бин, для окна Хеннинга 3 бина, для окна Кайзера 7 бин.
Заключение
При использовании метода СВЗ для измерения задержек и дистанций существует возможность повысить точность измерений применением метода «вилочных» отсчётов. Разработано теоретическое обоснование метода «вилочных» отсчётов и предложен метод вычисления оптимального значения ширины «вилочного» интервала. Проведена модельная и экспериментальная проверка полученных в работе результатов. Единственное ограничение на применение метода состоит в его более высокой, нежели метод поиска максимума, чувствительности к помехам, частоты которых близки к частоте полезного сигнала.
Рецензенты:Хранилов В.П., д.т.н., профессор, профессор кафедры «Компьютерные технологии в проектировании и производстве», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Кондратьев В.В., д.т.н., профессор, профессор кафедры «Вычислительные системы и технологии», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Библиографическая ссылка
Мартынюк М.В., Капранов С.Н. УВЕЛИЧЕНИЕ ТОЧНОСТИ ПРИ ИЗМЕРЕНИЯХ ПО МЕТОДУ СПЕКТРОМЕТРИИ ВРЕМЕННЫХ ЗАДЕРЖЕК // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16492 (дата обращения: 23.02.2026).



