Результаты и обсуждение
Главной проблемой использования нечетких регуляторов в мехатронных системах является создание базы правил нечеткого регулятора, позволяющей составить непротиворечивую систему продукционных правил, описывающую взаимосвязь между входными и выходными нечеткими переменными. Для решения этой проблемы существует три группы методов: текстологические, коммуникативные и группа методов Data Mining [8-10]. Текстологические методы предполагают изучение специальных текстов из учебников, монографий, статей, методик и других носителей профессиональных знаний. Главная сложность в этом случае заключается в принципиальной невозможности совпадения понимания информации, заложенной автором в текст и получаемой читателем. Коммуникативные методы позволяют построить нечеткий регулятор в процессе непосредственного общения эксперта и инженера по знаниям. Недостатки этих методов относятся к высокому субъективизму экспертной оценки, возможной предвзятости эксперта, неоднозначности информации по данному вопросу [9]. Группа Data Mining – это методы автоматизированного поиска в больших объемах данных неочевидных, объективных и полезных на практике закономерностей [8]. Одним из них является построение нечеткого регулятора с помощью генетических алгоритмов. Существенным преимуществом этого метода является его простота и устойчивость при поиске оптимального решения [10].
Предлагаемый процесс построения нечеткого регулятора реализован в двух компьютерных программах «Построение нечеткого регулятора эволюционными методами» и «Автоматическое обучение нечетких регуляторов MISO-типа» [6, 7], которые позволяют подобрать параметры для системы управления с несколькими входными переменными и одной выходной. Такие системы применяются в различных сферах деятельности человека.
Совокупность настраиваемых параметров нечеткого регулятора, упорядоченных специальным образом, таких как значения параметров терм-множеств входных и выходных переменных и весовые коэффициенты правил нечеткой продукции, можно рассматривать как особь или хромосому для генетического алгоритма. Построение нечеткого регулятора с помощью генетических алгоритмов предопределяет необходимость выполнения следующих этапов:
1) выбор функции приспособленности;
2) определение количества входных и выходных нечетких переменных и диапазона их возможных значений;
3) установление количества термов и их функций принадлежности для каждой переменной;
4) задание количества генераций случайных чисел.
Первый этап. Функция приспособленности как некий аналог целевой функции выбирается с учетом того, какой показатель мехатронной системы необходимо оптимизировать.
Второй этап. Входные нечеткие переменные определяются как управляемые величины системы управления. В качестве выходных нечетких переменных выступает одно или несколько управляющих воздействий. Диапазоном возможных значений переменных регулятора является множество значений между минимальным и максимальным значением переменной, определяемыми содержанием задачи.
Третий этап. Размер терм-множества нечетких переменных определяет объем базы правил и усложняет процесс работы регулятора, поэтому выбирать большое количество термов нецелесообразно. Большое влияние на значение функции приспособленности оказывает выбор типа функции принадлежности переменных нечеткого регулятора [1]. Чаще всего применяются следующие типы функций принадлежности: треугольная, трапецеидальная, функция Гаусса, гладкая и линейная s- и z-функция [9]. В таблице представлены возможные сочетания этих типов функций принадлежности, реализованные в программах [6, 7].
Таблица
Возможные сочетания типов функций принадлежности
|
№ |
Крайний левый терм |
Средние термы |
Крайний правый терм |
|
1 |
Трапецеидальная функция |
Треугольная функция |
Трапецеидальная функция |
|
2 |
Гладкая z-функция |
Функция Гаусса |
Гладкая s-функция |
|
3 |
Линейная z-функция |
Треугольная функция |
Линейная s-функция |
|
4 |
Гладкая z-функция |
Треугольная функция |
Гладкая s-функция |
|
5 |
Трапецеидальная функция |
Функция Гаусса |
Трапецеидальная функция |
|
6 |
Линейная z-функция |
Функция Гаусса |
Линейная s-функция |
Четвертый этап. Количество генераций случайных чисел зависит от характеристик генетического алгоритма, которые определяют число наборов параметров нечеткого регулятора, полученных путем скрещивания, мутацией двух элитных комбинаций и сгенерированных случайным образом. Скрещивание представляет собой получение двух новых комбинаций параметров, полученных путем инверсии элементов при дихотомическом делении элитных наборов случайным образом. Мутация заключается в изменении на некоторую величину случайно выбранного элемента одного из элитных наборов параметров.
Операции, представленные в описании четвертого этапа построения нечеткого регулятора, производятся над хромосомой (вектором параметров регулятора) заданное количество раз, в результате чего формируется популяция особей, или, иными словами, совокупность значений параметров. При отборе особей в следующую популяцию используется стратегия элитизма. Элитными считаются особи, для которых накопленная ошибка является наименьшей при использовании соответствующего нечеткого регулятора. При формировании последующей популяции над элитными хромосомами выполняются те же операции, что и для предыдущей популяции. Процесс продолжается до тех пор, пока не будет достигнут критерий окончания алгоритма, которым служит выполнение заданного количества итераций, называемых поколениями.
Генетический алгоритм дает удовлетворительные результаты уже в 5-7 поколении. Наилучшие результаты получаются примерно в 50-60 поколениях. Требуемая продолжительность выполнения алгоритма определяется длиной хромосомы, т.е. количеством параметров формируемого нечеткого регулятора, так как, сложность решаемой задачи пропорциональна сложности структуры нечеткого регулятора.
Представленные этапы формирования нечеткого регулятора посредством генетических алгоритмов иллюстрируются авторами на примерах подбора параметров регуляторов при решении двух задач: классической задачи теории управления о стабилизации вертикального положения перевернутого маятника и задачи оптимизации цикла светофорного регулирования для перекрестка с большим количеством направлений движения.
Вертикальный стержень, установленный на каретке в положении, когда центр масс находится выше точки опоры, представляет собой обращенный (перевернутый) маятник. Маятник имеет верхнее неустойчивое положение равновесия, поэтому при внешнем воздействии и каретка приходит в движение по горизонтальной поверхности, в результате чего стержень отклоняется от вертикального положения на угол φ. Для возвращения стержня в исходное положение необходимо определенным образом управлять воздействием. Изменение значения угла φ при движении каретки описывается системой дифференциальных уравнений второго порядка [1]:
![]()
![]()
где М – масса каретки, m – масса стержня, b – коэффициент вязкого трения каретки, l – расстояние от начала оси вращения стержня до центра масс стержня, J – момент инерции стержня, x – позиция каретки, φ – угол между стержнем и верхним вертикальным положением маятника, u – управляющее воздействие на маятник, имеющее размерность силы. В качестве функции приспособленности была выбрана сумма интегралов модулей координаты положения каретки х, и угла отклонения от вертикали φ. Входными переменными выступили координата положения каретки х и угол отклонения от вертикали φ, а выходной переменной – внешнее воздействие на каретку, имеющее размерность силы u [5].
Для построения нечеткого регулятора управлением движением перевернутого маятника применялись все перечисленные в таблице 1 сочетания видов терм-множеств, однако, наименьшее значение функции приспособленности наблюдалось при сочетании №4 [2]. Выполнение генетического алгоритма для построения нечеткого регулятора производилось при следующих заданных параметрах: в каждой популяции формировалось по 30 наборов хромосом, полученных скрещиванием и мутацией, и 40 – сгенерированных случайным образом. Количество поколений генетического алгоритма было принято равным 10 [5]. Результат стабилизации маятника показан на рис. 1.
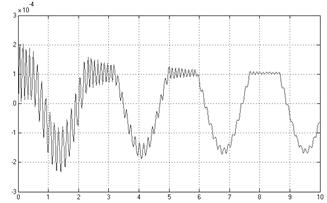
Рис. 1. Угол отклонения
перевернутого маятника от верхнего равновесного положения
при работе регулятора после оптимизации
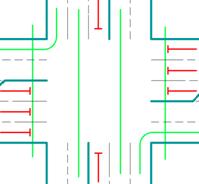
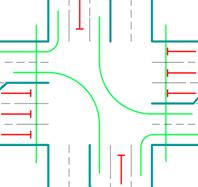
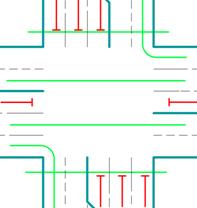
В модели перекрестка описано движение транспортных потоков на Х-образном перекрестке с тремя полосами движения по каждому из направлений. Таким образом, общее количество транспортных потоков на перекрестке равняется 12. Эти потоки распределены между четырьмя фазами светофорного цикла. Схема организации движения на описываемом перекрестке представлена на рис. 2.
|
Фаза 1 |
Фаза 2 |
|
Фаза 3 |
Фаза 4 |
Рис. 2. Схема организации движения
Для каждого из направлений движения задаются интенсивности транспортных потоков и потоки насыщения (пропускные способности), определяемые как количество автомобилей, проезжающих через перекресток за час (ав./час). Интенсивности потоков задают количество транспортных средств, подъезжающих к перекрестку за любой заданный промежуток времени, а пропускные способности, соответственно – какое количество автомобилей может проехать через перекресток за время горения разрешающего сигнала светофора. Таким образом, в течение каждой из фаз формируются очереди из транспортных средств перед стоп-линией. Задача управления параметрами светофорного цикла (длительностями фаз) состоит в минимизации общего количества автомобилей, ожидающих проезда перед перекрестком. Для этой цели авторами предложено использовать нечеткий регулятор [3, 4].
В модели задается минимальная продолжительность каждой из фаз. После ее завершения модель обращается к нечеткому регулятору, который определяет, требуется ли продление текущей фазы и, если да, то – на какое время. Регулятор определяет эту величину, исходя из состояния входных параметров и на основании базы знаний.
Так как транспортные потоки собранны в четыре группы, то в качестве входных параметров регулятора было выбрано суммарное количество транспортных средств, ожидающих проезда перекрестка в каждой из этих групп. Таким образом, регулятор имеет четыре входные переменные. При этом первая входная переменная – это количество автомобилей, которым для проезда нужна текущая фаза, вторая переменная – автомобили, ожидающие следующую фазу, третья – те автомобили, которые вынужденные стоять в ожидании разрешающего сигнала в течение этой и следующей фазы, и т.д. Диапазон значений каждой из входных переменных – от 0 до 150 автомобилей.
Выходная переменная нечеткого регулятора – время, на которое будет продлена текущая фаза, задаваемое в секундах. Диапазон выходной переменной – от 0 до 20 секунд. Количество термов для каждой из переменных выбрано равным пяти. Крайние левые и крайние правые термы представлены в виде трапецеидальных функций принадлежности, средние – треугольных. В качестве функции приспособленности для генетического алгоритма оптимизации параметров нечеткого регулятора принято суммарное количество транспортных средств, находящихся перед стоп-линиями перекрестка в течение заданного промежутка времени.
В настоящее время авторами проводятся эксперименты с моделью с целью определения оптимального сочетания параметров генетического алгоритма.
Заключение
Построение нечетких регуляторов с использованием генетических алгоритмов позволяет обеспечить высокую точность работы мехатронных систем. Предложенный процесс упрощает проектирование нечеткого регулятора, устанавливающего взаимосвязь выходных переменных с большим числом входных переменных. Единственным ограничением выступает мощность компьютера, выполняющего настройку параметров. Выходное пространство решений формируется только на основе входных воздействий. Это может быть удобно в случае отсутствия или чрезвычайной сложности описания объекта, а также в случае, если число входных и выходных параметров объекта достаточно велико.
Достоинством данного алгоритма построения является то, что он позволяет компенсировать потери информации об объекте управления, возникающие при передаче экспертного знания проектировщику, а в перспективе, возможно, отказаться от привлечения экспертов к процессу создания баз правил нечетких регуляторов. Основной недостаток заключается в возможных затруднениях интерпретации полученных параметров терм-множеств в некоторых ситуациях.
Рецензенты:Долгий Ю.Ф., д.ф.-м.н., профессор кафедры механики и математического моделирования Института математики и компьютерных наук Уральского федерального университета, г.Екатеринбург;
Готлиб Б.М., д.т.н., профессор кафедры «Мехатроника» Уральского государственного университета путей сообщения, г.Екатеринбург.
Библиографическая ссылка
Тарасян В.С., Куликова И.В., Мезенцев И.С. ПОСТРОЕНИЕ СИСТЕМЫ НЕЧЕТКОГО УПРАВЛЕНИЯ В МЕХАТРОННЫХ СИСТЕМАХ ПРИ ПОМОЩИ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16429 (дата обращения: 18.02.2026).