С увеличением количества вычислительных элементов в современных процессорах вычислительные системы приобретают все большую степень параллелизма. Разработка вычислительного программного кода, способного эффективно задействовать возможности аппаратуры, всегда являлась сложной задачей. Сегодня одним из актуальных подходов решения данной задачи является автоматическое распараллеливание программ.
Большинство вычислительно емких научных и инженерных приложений тратят значительную часть времени исполнения на вложенности циклов, часто отвечающие критериям линейности программ. Модель многогранников [8] предоставляет мощный математический аппарат, упрощающий анализ и преобразование таких программ с целью улучшения быстродействия путем повышения параллелизма и оптимизации локальности данных при вычислениях.
Методы модели многогранников широко используются в статической компиляции. Код, написанный на языке высокого уровня (чаще всего это C или FORTRAN), оптимизируется для параллельного выполнения и компилируется для целевой архитектуры.
Распараллеливание в модели многогранников осуществляется в пять этапов.
1. Анализ зависимостей операций по данным. Рассматриваются потоковые зависимости (чтение после записи), антизависимости (запись после чтения), зависимости через выход (запись после записи).
2. Поиск для каждой операции функции расписания, сохраняющей логический порядок операций в соответствии с зависимостями по данным.
3. Поиск для каждой операции функции размещения, ставящей в соответствие операции индекс виртуального процессора.
4. Разбиение индексного пространства виртуальных процессоров — сопоставление виртуальных процессоров физическим.
5. Генерация параллельной программы по алгоритму [1] в соответствии с пространственно-временным преобразованием, заданным функциями расписания и размещения, и разбиением.
Широко применяемыми на практике стали классические методы поиска расписаний, ориентированные на минимизацию задержки расписания [6, 7] (поиск расписаний с наибольшим параллелизмом), и современный подход [3], ориентированный на минимизацию задержки использования данных (поиск расписаний, обеспечивающих временную локальность данных для более эффективного использования кэшей процессоров).
Подход к оптимизации временной локальности данных, предложенный в работе [3] и реализованный в компиляторе Pluto, демонстрирует эффективность на практике [2]. Однако, метод, его реализующий, не лишен следующего конструктивного недостатка: поскольку задача сводится к поиску лексикографического минимума на многограннике [5], возникает вопрос о порядке следования переменных в целевом векторе, или, в терминах теории принятия решений, вопрос о предпочтениях ЛПР (лица, принимающего решение) относительно качества оптимизации для каждой зависимости по данным. Кроме того, в такой постановке задачи оптимизации невозможно задать одинаковый приоритет различным зависимостям, поскольку невозможно поставить две переменные на одну и ту же позицию в целевом векторе.
Метод, предложенный в настоящей работе, базируется на той же идее сокращения задержки использования данных для более эффективного использования кэшей процессоров, но предоставляет более гибкие средства задания предпочтений ЛПР, не исключая из рассмотрения оптимальные решения, достижимые по методу [3].
1. Базовые понятия модели многогранников
Модель многогранников рассматривает класс линейных программ и полагается на поиск расписаний в аффинном виде. Эти программы удовлетворяют следующим ограничениям:
-
единственным типом исполнительного оператора может быть оператор присваивания, правая часть которого является арифметическим выражением;
-
все повторяющиеся операции описываются только с помощью циклов DO языка FORTRAN (либо эквивалентными циклами for языка С); структура вложенности циклов может быть произвольной; шаги изменения параметров циклов всегда равны +1;
-
допускается использование условных и безусловных операторов перехода, передающих управление «вниз» по тексту; не допускаются побочные выходы из циклов;
-
все индексные выражения переменных, границы изменения параметров циклов и условия передачи управления задаются неоднородными формами, линейными по совокупности параметров циклов и внешних переменных программы; все коэффициенты линейных форм являются целыми числами;
-
внешние переменные программы всегда целочисленные; конкретные значения внешних переменных известны только во время работы программы.
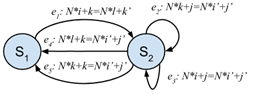
Обобщенный граф зависимостей — это ориентированный мультиграф, каждая вершина которого представляет множество соответственных операций (динамических экземпляров одной и той же инструкции). Каждая операция принадлежит только одной вершине. Ребро графа представляет временное ограничение на две операции, соответствующие начальной и конечной вершине (принцип причинности для информационно зависимых операций ![]() и
и ![]() :
: ![]() , где
, где ![]() – логическое время). В обобщенном графе зависимостей могут быть петли и циклы. Каждая вершина помечается описанием соответствующих операций, а каждое ребро — описанием соответствующих отношений зависимости.
– логическое время). В обобщенном графе зависимостей могут быть петли и циклы. Каждая вершина помечается описанием соответствующих операций, а каждое ребро — описанием соответствующих отношений зависимости.
Каждой вершине ![]() соответствует ее домен – многогранник
соответствует ее домен – многогранник ![]() на множестве
на множестве ![]() , где
, где ![]() – размерность ее итерационного пространства (количество циклов в программе, включающих
– размерность ее итерационного пространства (количество циклов в программе, включающих ![]() ). Каждая операция представляется как
). Каждая операция представляется как ![]() , где
, где ![]() – целочисленный вектор индекса итерации,
– целочисленный вектор индекса итерации, ![]() – целочисленный вектор внешних переменных программы.
– целочисленный вектор внешних переменных программы.
Каждому ребру ![]() , исходящему из вершины
, исходящему из вершины ![]() в
в ![]() , ставится в соответствие многогранник
, ставится в соответствие многогранник ![]() на множестве
на множестве ![]() такой, что условие причинности должно быть наложено на динамические экземпляры операций
такой, что условие причинности должно быть наложено на динамические экземпляры операций ![]() и
и ![]() тогда и только тогда, когда для составного вектора
тогда и только тогда, когда для составного вектора ![]() выполняется
выполняется ![]() .
.
Пусть ![]() и
и ![]() – индексные функции ячейки памяти, к которой обращаются конфликтующие операции, тогда
– индексные функции ячейки памяти, к которой обращаются конфликтующие операции, тогда ![]() называют глубиной зависимости:
называют глубиной зависимости:
![]()
Расписание для обобщенного графа зависимостей есть неотрицательная функция ![]() такая, что
такая, что ![]()
2. Минимизация задержки использования данных в модели многогранников
Пусть обобщенный граф зависимостей анализируемой программы содержит ![]() вершин
вершин ![]() ,
, ![]() и
и ![]() ребер
ребер ![]() ,
, ![]() . Требуется найти расписание
. Требуется найти расписание ![]() , минимизирующее задержку использования данных для каждого ребра
, минимизирующее задержку использования данных для каждого ребра ![]() ,
, ![]() :
: ![]() .
.
Требования приводят к следующей формулировке задачи многокритериальной оптимизации. Определим множество исходов (совпадающее со множеством альтернатив):
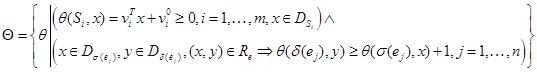 .
.
Здесь ![]() – вектор-столбец из
– вектор-столбец из ![]() элементов,
элементов, ![]() – скаляр (значения принадлежат множеству
– скаляр (значения принадлежат множеству ![]() ),
), ![]() – аффинная функция расписания для инструкции
– аффинная функция расписания для инструкции ![]() (
(![]() ).
).
Показатели качества решения задаются ![]() функциями
функциями ![]() ,
, ![]() , которые требуется минимизировать:
, которые требуется минимизировать: ![]() .
.
Будем искать эффективный вектор ![]() как оптимальное по Парето решение, применив технику линейной свертки:
как оптимальное по Парето решение, применив технику линейной свертки: ![]() , где
, где ![]() – весовые коэффициенты, отражающие предпочтения ЛПР относительно качества оптимизации для каждой зависимости по данным. Такая формулировка позволяет точнее отразить предпочтения ЛПР в силу большей гибкости относительно [3].
– весовые коэффициенты, отражающие предпочтения ЛПР относительно качества оптимизации для каждой зависимости по данным. Такая формулировка позволяет точнее отразить предпочтения ЛПР в силу большей гибкости относительно [3].
Для программ со слабой параметризацией, или в случае Just-In-Time компиляции, когда значения внешних переменных программы становятся известными, становится возможной приоритезация зависимостей на основе частоты возникновения ситуаций доступа к одной ячейке памяти: ![]() , где
, где ![]() – количество точек с целочисленными координатами внутри многогранника зависимостей
– количество точек с целочисленными координатами внутри многогранника зависимостей ![]() , которое может быть вычислено с помощью алгоритма Клаусса [4], реализованного в библиотеке PolyLib [9]. Такая постановка реализует естественную эвристику: ЛПР заинтересовано в наилучшем качестве оптимизации для тех зависимостей, которые чаще возникают.
, которое может быть вычислено с помощью алгоритма Клаусса [4], реализованного в библиотеке PolyLib [9]. Такая постановка реализует естественную эвристику: ЛПР заинтересовано в наилучшем качестве оптимизации для тех зависимостей, которые чаще возникают.
Для каждого ребра ![]() наложим ограничения на функции расписания инструкций
наложим ограничения на функции расписания инструкций ![]() и
и ![]() , затем составим систему из всех этих ограничений:
, затем составим систему из всех этих ограничений:
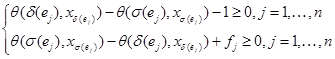 .
.
Первое ограничение обусловлено принципом причинности, второе задает лимит задержки использования, который требуется минимизировать. Линеаризуем систему ограничений с помощью классической техники на основе леммы Фаркаша.
Лемма Фаркаша. Пусть ![]() – непустой многогранник, определённый с помощью
– непустой многогранник, определённый с помощью![]() аффинных неравенств (граней):
аффинных неравенств (граней): ![]() . Аффинная форма
. Аффинная форма ![]() неотрицательна в любой точке
неотрицательна в любой точке ![]() тогда и только тогда, когда она является неотрицательной аффинной комбинацией:
тогда и только тогда, когда она является неотрицательной аффинной комбинацией: ![]() . Неотрицательные константы
. Неотрицательные константы ![]() называются множителями Фаркаша.
называются множителями Фаркаша.
Для каждой инструкции ![]() выписывается шаблон функции расписания, неотрицательной внутри ее домена:
выписывается шаблон функции расписания, неотрицательной внутри ее домена: 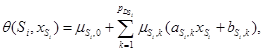 где
где ![]() – множители Фаркаша, а
– множители Фаркаша, а ![]() неравенств
неравенств ![]() определяют домен
определяют домен ![]() ,
, ![]() .
.
Применим лемму Фаркаша для каждого ограничения:
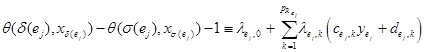
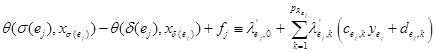
Здесь ![]() и
и ![]() – множители Фаркаша, а
– множители Фаркаша, а ![]() неравенств
неравенств ![]() определяют многогранник зависимостей
определяют многогранник зависимостей ![]() ,
, 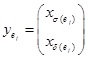 – составной вектор индексов для обеих инструкций
– составной вектор индексов для обеих инструкций ![]() в
в ![]() ,
,![]() . В итоге система ограничений примет вид:
. В итоге система ограничений примет вид:
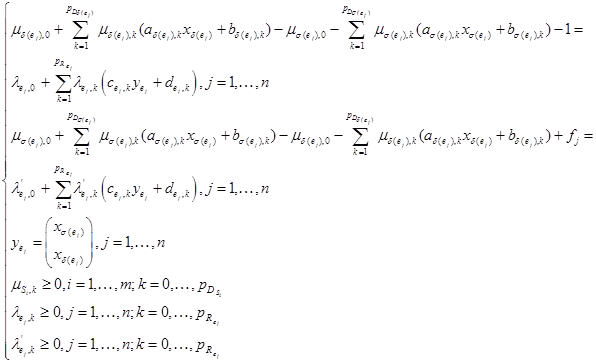
Приравнивание соответственных множителей при компонентах векторов ![]() в левых и правых частях ограничений позволяет оставить в системе только множители Фаркаша
в левых и правых частях ограничений позволяет оставить в системе только множители Фаркаша ![]() и переменные-ограничители
и переменные-ограничители ![]() .
.
Поиск Парето-оптимального решения задачи многокритериальной оптимизации сводится к решению задачи линейного целочисленного программирования с целевой функцией ![]() , которую требуется минимизировать при сформированной системе ограничений (без участия компонентов векторов
, которую требуется минимизировать при сформированной системе ограничений (без участия компонентов векторов ![]() в качестве переменных):
в качестве переменных):
![]() , где
, где ![]() – весовые коэффициенты, отражающие предпочтения ЛПР относительно качества оптимизации для каждой зависимости по данным. В случае слабой параметризации программы или Just-In-Time компиляции целесообразно взять
– весовые коэффициенты, отражающие предпочтения ЛПР относительно качества оптимизации для каждой зависимости по данным. В случае слабой параметризации программы или Just-In-Time компиляции целесообразно взять ![]() , что обеспечит больший приоритет зависимостям, которые чаще возникают.
, что обеспечит больший приоритет зависимостям, которые чаще возникают.
Решение задачи ЛЦП может быть осуществлено, например, методом ветвей и границ, реализованным в библиотеке GNU Linear Programming Kit [10]. Подстановка значений ![]() в соответствующие шаблоны функций расписания для каждой инструкции дает решение задачи поиска расписания
в соответствующие шаблоны функций расписания для каждой инструкции дает решение задачи поиска расписания ![]() .
.
3. Распараллеливание LU-разложения
Рассмотрим алгоритм LU-разложения с его информационными зависимостями (рисунок 1) и найдем два расписания, используя разработанный метод.
|
for (int k = 0; k < N; k++) { for (int j = k + 1; j < N; j++) A[j * N + k] /= A[k * N + k]; //S1 for (int i = k + 1; i < N; i++) for (int j = k + 1; j < N; j++) A[i * N + j] -= A[i * N + k] * A[k * N + j]; //S2 } |
|
Рис. 1. Код LU-разложения на языке C и обобщенный граф зависимостей
Ослабим параметризацию программы, зафиксировав ![]() . Изменяя коэффициенты в целевой функции задачи ЛЦП можно управлять задержкой использования данных: например, для
. Изменяя коэффициенты в целевой функции задачи ЛЦП можно управлять задержкой использования данных: например, для ![]() функции расписания примут вид
функции расписания примут вид ![]() и
и ![]() (при этом
(при этом ![]() ), а для
), а для ![]() получаем
получаем ![]() и
и ![]() (при этом
(при этом ![]() ; именно такое расписание находит компилятор Pluto [2]).
; именно такое расписание находит компилятор Pluto [2]).
Эксперименты на четырехъядерном процессоре Intel Core i7 930 показывают ускорение от распараллеливания в 3,96 раза для ![]() и
и ![]() , и ускорение в 3,21 раза для
, и ускорение в 3,21 раза для ![]() и
и ![]() , что свидетельствует об эффективности разработанного метода и целесообразности более точного задания системы предпочтений ЛПР.
, что свидетельствует об эффективности разработанного метода и целесообразности более точного задания системы предпочтений ЛПР.
Заключение
В ходе исследования была показана необходимость совершенствования способа задания системы предпочтений ЛПР для того, чтобы повысить качество оптимизации временной локальности данных при автоматическом распараллеливании линейных программ. Предложен метод поиска расписания, минимизирующего задержку использования данных для каждой информационной зависимости. Рассмотрение задачи поиска расписания как задачи многокритериального выбора в условиях полной определенности позволяет задать линейную свертку критериев качества, точнее отражающую систему предпочтений ЛПР и потому позволяет находить более удачные (в плане повышения быстродействия синтезированной параллельной программы) расписания, чем распространенный на момент исследования метод [3], опирающийся на технику поиска лексикографического минимума на многограннике.
Работа выполнена в рамках проекта РФФИ №14-37-50316 «Исследование и разработка методов автоматического распараллеливания программ для гетерогенных вычислительных систем и систем с распределенной памятью» при финансовой поддержке Фонда.
Рецензенты:
Хачумов В.М., д.т.н., профессор, зав. лабораторией интеллектуального управления, ФГБУН Институт системного анализа Российской академии наук, г. Москва;
Цирлин А.М., д.т.н., профессор, зам. директора по научной работе ФГБУН Институт программных систем им. А.К. Айламазяна Российской академии наук, Ярославская обл., с. Веськово.
Библиографическая ссылка
Лебедев А.С. ОПТИМИЗАЦИЯ ВРЕМЕННОЙ ЛОКАЛЬНОСТИ ДАННЫХ ПРИ АВТОМАТИЧЕСКОМ РАСПАРАЛЛЕЛИВАНИИ ЛИНЕЙНЫХ ПРОГРАММ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16255 (дата обращения: 23.02.2026).