Формирование изображений, улучшение качества и автоматизация обработки медицинских изображений, включая изображения, создаваемые электронными микроскопами, рентгеновскими аппаратами, томографами и т.д., являются предметом исследования и разработки. Сегодня в медицинской технике широко применяются системы формирования изображения, его преобразования в цифровую форму, визуализация и документирование путем введения в компьютер изображений с помощью специализированных устройств захвата видео. Автоматический анализ в системах дистанционного наблюдения широко применяется при анализе местности, в лесном хозяйстве, например, для автоматического подсчета площади вырубок, в сельском хозяйстве для наблюдения за созреванием урожая, при разведке, в системах противопожарной безопасности. Контроль качества производимой продукции выполняется благодаря автоматическим методам анализа сцен. Компьютерная обработка изображений применяется в задачах экспертизы живописи неразрушающими методами. Для восстановления старых фильмов применяются методы автоматической компенсации дефектов видеоматериала, полученного после преобразования киноизображения в видео.
Изображения, полученные на выходе оптико -электронных преобразователей, искажены помехами. Это затрудняет как визуальный анализ изображений человеком - оператором, так и их автоматическую компьютерную обработку. При обработке изображений помехами являются и некоторые области самого изображения. Например, при анализе объектов на сложном фоне, фон тоже представляет собой помеху. При цифровой обработке изображений необходимо устранять геометрические искажения изображений, подавлять шумы различной природы, производить апертурную коррекцию. Ослабление действия помех достигается фильтрацией.
Решение задачи выделения контуров используется в промышленности при создании автономных роботов, а также систем анализа изображений в сложных условиях наблюдения, при воздействии различных мешающих факторов, усложняющих процесс регистрации изображения и при отсутствии априорных сведений о виде фоновых шумов. Это значит, что методы и алгоритмы обработки информации с датчиков изображения должны учитывать наличие шумов различной природы, связанных с регистрацией изображений и сигналов в реальных системах. При этом известные в настоящее время алгоритмы решения таких задач предполагают предварительную фильтрацию изображений, а затем решение задачи выделения контуров. При построении методов и алгоритмов фильтрации изображений требуется априорное знание характеристик искажающих помех. На практике, в большинстве случаев такая информация отсутствует или является приближенной.
Смысл операции подчеркивания контуров состоит в том, чтобы усилить резкие перепады яркости, сформировав в соответствующих точках кадра импульсные отклики на фоне сравнительно слабых флюктуации в других областях картины, не содержащих крутых яркостных перепадов. По своему характеру все операторы подчеркивания контуров являются различными модификациями дифференцирования двумерного поля по различным направлениям области определения. Как известно, при дифференцировании, в самом деле, в окрестности перепада функции яркости образуется пик, способствующий регистрации этой области. Однако также хорошо известно, что при дифференцировании сигналов с помехами происходит существенное усиление последних, что снижает отношение сигнал/шум и негативно отражается на получаемых результатах.
Обычно оператор подчеркивания контуров представляют в форме масочного линейного фильтра. В процессе обработки маска, которая является просто матрицей коэффициентов, скользит по полю изображения, занимая поочередно все возможные положения. В каждом положении маска играет роль окна, при помощи которого отбираются отсчеты обрабатываемого изображения и выполняется их поэлементное умножение на соответствующий элемент маски с последующим суммированием всех произведений. Полученное число рассматривается как отсчет выходного изображения в точке, соответствующей центру симметрии окна.
Отмеченное выше делает вполне очевидной актуальность проведения исследований существующих и создания новых методов цифрового дифференцирования сигналов и изображений, зарегистрированных на фоне шума, а также выбора такого или таких из них, которые наиболее пригодны для реализации с применением средств современной микропроцессорной техники и позволяющие достичь требуемых характеристик и не требующих знания априорных характеристик помех и фоновых шумов.
Таким образом, научная задача разработки алгоритмов автоматизированного анализа результатов измерений для выделения контуров объектов в изображениях при наличии фонового шума и их программная реализация в настоящее время не решена в достаточной мере, и является актуальной.
Рассмотрим подробнее алгоритмы вейвлет-дифференцирования с использованием вейвлетов MHAT DOG WAVE, полученные на основе разработанного ранее метода вейвлет-дифференцирования [1, 2, 3]. В общем виде производные строки и столбца изображений могут быть записаны в следующем виде:
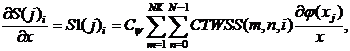 (1)
(1)
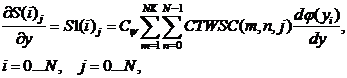 (2)
(2)
где ![]() и
и ![]() соответственно коэффициенты прямого
дискретного вейвлет-преобразования по строкам и столбцам матрицы
соответственно коэффициенты прямого
дискретного вейвлет-преобразования по строкам и столбцам матрицы ![]()
![]() (3)
(3)
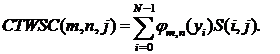 (4)
(4)
Тогда выражение для квадрата градиента матрицы ![]() будет иметь следующий вид:
будет иметь следующий вид:
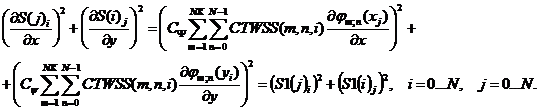 (5)
(5)
Модуль градиента интенсивности исследуемого изображения ![]() в терминах вейвлет-преобразования
запишется в следующем виде:
в терминах вейвлет-преобразования
запишется в следующем виде:
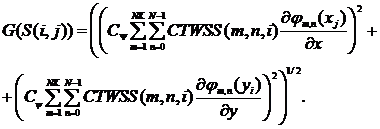 (6)
(6)
Изображения в процессе формирования их изображающими системами (фотографическими, голографическими, телевизионными) обычно подвергаются воздействию различных случайных помех или шумов. Наиболее распространенным видом помех является случайный аддитивный шум, статистически независимый от сигнала. Модель аддитивного шума хорошо описывает действие зернистости фотопленки, шум квантования в аналого-цифровых преобразователях и т.п. Поэтому при проведении математического моделирования будем использовать датчик случайных чисел, при этом критерии оценки качества выделения контуров изображений должны быть статистическими.
В качестве критериев в работе использованы следующие.
1. Среднеквадратическое отклонение ![]() :
:
![]()
![]()
![]()
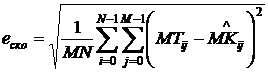
![]() (7)
(7)
При этом в качестве тестового изображения MT использовалось изображение
контуров, полученное из незашумленного исследуемого изображения S детектором границ Canny.
В дальнейшем на исходное изображение S накладывался аддитивный
гауссовский шум и проводилось определение контуров предложенным методом
вейвлет-дифференцирования и известным методом Собеля.
При этом были получены изображения ![]() .
.
2. Отношение пиковый сигнал/шум SNRGG:
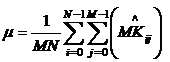 ;
; 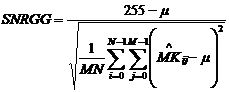 ; (8)
; (8)
где ![]() -
среднее значение
-
среднее значение ![]() .
.
3. Отношение пиковый сигнал/шум SNRF (с использованием в расчетах СКО фона):
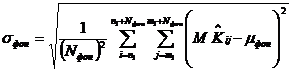 ; (
9)
; (
9)
где:![]() - СКО фона;
- СКО фона; 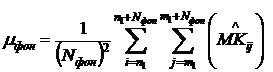 -
среднее значение фона; n1, m1- координаты выбранной
площадки фона размером
-
среднее значение фона; n1, m1- координаты выбранной
площадки фона размером ![]() на исследуемом изображении
на исследуемом изображении
![]() ,
, 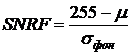 .
(10)
.
(10)
Используя три критерия, в дальнейшем можно будет более адекватно оценить эффективность предложенных алгоритмов по сравнению с известными.
Для качественной и количественной разработанных алгоритмов проведем проверку их функционирования на тестовых изображениях. Порядок проведения вычислительного эксперимента был следующим [4, 5, 6]. Исходное восьмибитное изображение размером 512*512 Lena было обработано детектором границ Canny. Затем изображение Lena подвергалось воздействию аддитивного гауссовского шума с СКО σ= 20, 30, 40, 50. В таблице приведены результаты для серии исследованных тестовых изображений.
Результаты вычислительных экспериментов
|
Среднеквадратическое отклонение 20 |
|
|
|
|
SKO |
82,77 |
83,6 |
79,81 |
|
SNRGG |
8,02 |
8,11 |
10,55 |
|
SNRF |
13,63 |
15,7 |
15,81 |
|
Выигрыш SKO по Собелю в Дб |
1,47 |
1,43 |
1,63 |
|
Выигрыш SKO по Никелю в Дб |
3,53 |
3,49 |
3,69 |
|
Выигрыш SNRGG по Собелю в Дб |
5,45 |
5,5 |
6,64 |
|
Выигрыш SNRGG по Никелю в Дб |
9,37 |
9,42 |
10,57 |
|
Выигрыш SNRF по Собелю в Дб |
7,75 |
8,37 |
8,4 |
|
Выигрыш SNRF по Никелю в Дб |
11,68 |
12,29 |
12,32 |
|
Среднеквадратическое отклонение 30 |
|
|
|
|
SKO |
82,59 |
84,33 |
79,74 |
|
SNRGG |
8,69 |
8,07 |
11,58 |
|
SNRF |
13,39 |
15,08 |
15,39 |
|
Выигрыш SKO по Собелю в Дб |
1,96 |
1,87 |
2,11 |
|
Выигрыш SKO по Никелю в Дб |
3,54 |
3,45 |
3,69 |
|
Выигрыш SNRGG по Собелю в Дб |
6,59 |
6,28 |
7,84 |
|
Выигрыш SNRGG по Никелю в Дб |
9,74 |
9,43 |
10,99 |
|
Выигрыш SNRF по Собелю в Дб |
8,47 |
8,99 |
9,08 |
|
Выигрыш SNRF по Никелю в Дб |
11,62 |
12,14 |
12,23 |
|
Среднеквадратическое отклонение 40 |
|
|
|
|
SKO |
84,15 |
84,28 |
80,17 |
|
SNRGG |
7,96 |
8,27 |
10,83 |
|
SNRF |
11,75 |
15,09 |
13,79 |
|
Выигрыш SKO по Собелю в Дб |
2,16 |
2,15 |
2,37 |
|
Выигрыш SKO по Никелю в Дб |
3,46 |
3,45 |
3,67 |
|
Выигрыш SNRGG по Собелю в Дб |
6,67 |
6,83 |
8,01 |
|
Выигрыш SNRGG по Никелю в Дб |
9,38 |
9,54 |
10,72 |
|
Выигрыш SNRF по Собелю в Дб |
8,36 |
9,45 |
9,06 |
|
Выигрыш SNRF по Никелю в Дб |
11,07 |
12,16 |
11,77 |
|
|
|
|
|
|
SKO |
83,78 |
84,96 |
80,26 |
|
SNRGG |
8,33 |
7,96 |
10,79 |
|
SNRF |
11,82 |
13,85 |
13,18 |
|
Выигрыш SKO по Собелю в Дб |
2,54 |
2,48 |
2,72 |
|
|
|
|
|
|
Выигрыш SKO по Никелю в Дб |
3,48 |
3,42 |
3,67 |
|
Выигрыш SNRGG по Собелю в Дб |
7,57 |
7,37 |
8,69 |
|
Выигрыш SNRGG по Никелю в Дб |
9,59 |
9,39 |
10,71 |
|
Выигрыш SNRF по Собелю в Дб |
9,08 |
9,78 |
9,56 |
|
Выигрыш SNRF по Никелю в Дб |
11,11 |
11,8 |
11,58 |
Выводы
Анализ представленных на рисунках изображений и результатов математического моделирования позволяет сделать следующие выводы. Предложенный метод обработки изображений позволяет эффективно выделять контуры изображений, искаженных шумом. Разработанные новый метод и алгоритмы вейвлет-дифференцирования изображений на фоне шума с использованием дискретного вейвлет- преобразования, позволяют повысить отношение пиковый сигнал-шум на 4,8÷9,6 дБ и на 3÷4 раза уменьшить среднеквадратическое отклонение ошибки.
В данном случае свойства вейвлет-преобразования позволяют отказаться от применения различных масок, то есть, по сути, отказаться от малоэффективных методов численного дифференцирования. На базе предложенного метода могут быть реализованы и другие алгоритмы выделения контуров на базе вейвлет-дифференцирования с использованием других вейвлетных базисов.
Рецензенты:Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Минобрнауки России, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Донской государственный технический университет», г. Ростов-на-Дону;
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС» г. Ростов-на-Дону.
Библиографическая ссылка
Безуглов Д.А., Кузин А.П., Швидченко С.А. АЛГОРИТМИЧЕСКИЕ МЕТОДЫ ВЕЙВЛЕТ-АНАЛИЗА ИЗОБРАЖЕНИЙ В УСЛОВИЯХ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ НА СЛУЧАЙНОМ ФОНЕ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16232 (дата обращения: 19.02.2026).



