Экспериментально изучается динамика трехфазной системы газ – жидкость – сыпучая среда в быстро вращающемся горизонтальном цилиндре. При быстром вращении цилиндра под действием центробежной силы инерции жидкость и тяжелая сыпучая среда переходят в центрифугированное состояние. Вследствие действия силы тяжести кольцевой слой жидкости оказывается неоднородным по толщине: в лабораторной системе отсчета воздушный цилиндр смещен вниз по отношению к оси вращения. Во вращающейся системе отсчета такое распределение жидкости соответствует распространению двумерной волны в направлении, противоположном вращению цилиндра со скоростью, равной скорости вращения кюветы Ω. Бегущая азимутальная волна генерирует в жидкости вынужденные колебания с частотой, равной скорости вращения цилиндра. Кроме того, под действием силы тяжести в жидкости могут возбуждаться инерционные волны, которые также становятся источником колебаний. Таким образом, колебательное движение жидкости является суперпозицией нескольких типов колебаний. В [3] обнаружено, что интенсификация колебательного движения жидкости приводит к формированию квазистационарного рельефа в форме холмов, перпендикулярных оси колебаний. Для выяснения механизма возникновения рельефа требуется изучить скорость колебательного движения жидкости.
Экспериментальная установка. Эксперименты проводятся с цилиндрической кюветой 1, установленной на горизонтальной платформе 2 (рис. 1). Кювета приводится во вращение с помощью шагового двигателя 3 типа FL86STH80-4208A с блоком управления SMD-40M. Скорость вращения регулируется генератором электрических сигналов Gw Instek GAG-810. В экспериментах скорость вращения варьируется в диапазоне f = 0 – 15 об/с, погрешность измерения f не превышает 0.01 об/с.
Кювета представляет собой полый прозрачный цилиндр кругового сечения из плексигласа длиной L = 7.8 см и внутренним диаметром D = 12.6 см. В центре одного из торцов кюветы имеется отверстие для заполнения жидкостью и сыпучей средой. После заполнения жидкостью и песком кювета крепится к платформе.
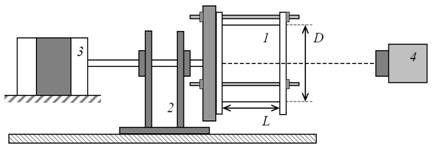
Рис. 1. Экспериментальная установка
В качестве рабочей жидкости используются водоглицериновые смеси различной концентрации, кинематическая вязкость которых варьируется в диапазоне n = 1 ? 30 сСт. Вязкость жидкости измеряется вискозиметром типа ВПЖ-2 (с точностью 0.1 сСт). Количество жидкости характеризуется величиной относительного наполнения q = V/V0, где V ? объем кольцевого слоя жидкости, V0 ? объем полости за вычетом объема кольцевого слоя песка. В экспериментах наполнение варьируется в диапазоне q = 0.1 – 0.6. Сыпучая среда представляет собой калиброванные сферические стеклянные частицы диаметром 150 – 250 мкм. В экспериментах масса сыпучей среды m равна 125 или 250 г. Плотность гранул измеряется методом гидростатического взвешивания и составляет ρ = 2.5 г/см3.
В кювету с жидкостью и сыпучей средой добавляются маркеры размером ~1 мм с плотностью, примерно равной плотности жидкости. Во вращающемся цилиндре маркеры располагаются внутри жидкости над сыпучей средой. Маркеры увлекаются потоками жидкости и используются для визуализации потоков и измерения скорости жидкости.
Движение жидкости изучается с использованием высокоскоростной видеокамеры Optronis CamRecord CL600x2 4, позволяющей производить регистрацию со скоростью до 1200 кадров в секунду при разрешении 800×600 пикселей. Наблюдения проводятся при естественном или стробоскопическом освещении через торцевую стенку кюветы. В зависимости от цели эксперимента частота вспышек стробоскопической лампы согласуется со скоростью вращения полости или со скоростью распространения инерционной волны. Управление стробоскопической лампой осуществляется с помощью ЦАП ZETLab с точностью 0.01 Гц.
Результаты эксперимента. При изучении динамики жидкости и сыпучей среды в быстро вращающемся горизонтальном цилиндре обнаружено, что граница раздела жидкость – песок неустойчива к появлению регулярного квазистационарного рельефа в виде вытянутых вдоль оси вращения холмов (рис. 2). Появление квазистационарного рельефа предположительно связано с неустойчивостью границы раздела в результате азимутального колебательного течения жидкости, возбуждаемого силой тяжести.
Интенсивность колебаний жидкости во вращающемся цилиндре определяется отношением силы тяжести и центробежной силы инерции [2]:
![]() , (1)
, (1)
здесь Ω = 2πf – угловая скорость вращения, a – радиус свободной поверхности жидкости, g – ускорение свободного падения. В отсутствие вращения жидкость и сыпучая среда находятся в нижней части полости. При плавном увеличении скорости вращения цилиндра жидкость и песок частично увлекаются вращающейся стенкой цилиндра. С увеличением скорости вращения объем увлекаемых стенкой жидкости и сыпучей среды возрастает. Сначала в центрифугированное состояние переходит сыпучая среда. При дальнейшем увеличении f жидкость также образует кольцевой слой (точки 1 на рис. 3). В быстро вращающемся горизонтальном цилиндре, когда действие силы тяжести мало по сравнению с центробежной силой инерции (Г << 1), жидкость почти равномерным слоем покрывают цилиндрическую стенку кюветы и совершают вынужденные азимутальные колебания под действием осциллирующей в системе отсчета полости силы тяжести. Помимо вынужденных колебаний в жидкости также могут возбуждаться колебания под действием азимутальных инерционных волн: порог их возникновения показан точками 2 на рис. 3.
В экспериментах [1] обнаружены бегущие инерционные волны с азимутальными волновыми числами k = 1 – 5. Фазовая скорость волн зависит от скорости вращения цилиндра и волнового числа k; амплитуда возрастает при уменьшении скорости вращения. При понижении скорости вращения на поверхности песка пороговым образом возникает пространственно–периодический рельеф (рис. 3, точки 3). Дальнейшее понижение скорости вращения полости приводит к потере устойчивости центрифугированного состояния жидкости и песка. При достижении пороговой скорости вращения центрифугированный слой обрушается на дно полости, рельеф разрушается (рис. 3, точки 4). Согласно наблюдениям колебательное движение жидкости вблизи границы раздела жидкость – сыпучая среда является причиной возникновения пространственно-периодического рельефа в виде холмов, вытянутых вдоль оси вращения. В зависимости от скорости Ω и относительного наполнения q жидкость совершает только вынужденные колебания или вынужденные и волновые колебания.

Рис. 2. Рельеф на границе раздела жидкость – сыпучая среда: Ω = 35.2 с-1, ν = 1.4 сСт, m = 250 г, q = 0.216; светлая линия демонстрирует границу раздела между жидкостью и воздухом; воздушный столб занимает центральную часть полости
С помощью программы CamRecord при заданной скорости вращения выполняется видеосъемка жидкости с имеющимися в ней маркерами в течение интервала времени, достаточного для нескольких десятков оборотов цилиндра. Полученный видеоряд сохраняется в виде серии файлов в формате JPG.
Для вычисления скорости колебательного движения жидкости относительно вращающейся полости вычисляется амплитуда колебаний жидкости b и их частота Ωosc: v0 = bΩosc. Для вычисления амплитуды колебаний с помощью программы MB-Ruler измеряется азимутальная координата маркера φ в жидкости относительно вертикали в зависимости от времени в течение нескольких десятков оборотов цилиндра. В таком случае положение маркера относительно вращающегося цилиндра может быть вычислено по формуле φ0 = φ – Ωt, здесь t – время. Время t можно вычислить, зная время между последовательными кадрами τ: t = (N – 1)τ, где N – номер фотографии в серии. На рис. 4а приведены результаты измерения φ0 в зависимости от угла поворота цилиндра θ = Ωt. Важно отметить, что помимо колебательного движения жидкость одновременно совершает осредненное азимутальное движение в направлении, противоположном вращению цилиндра, о чем свидетельствуют уменьшение угла φ0 на рис. 4а. Осредненное азимутальное движение жидкости во вращающемся цилиндре подробно изучено в [2], и здесь мы не будем останавливаться на его обсуждении. Отметим только, что осредненное течение жидкости становится важным в надкритической области существования рельефа, где приводит к его азимутальному дрейфу.
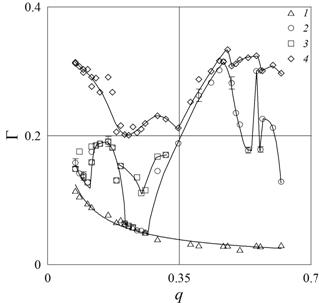
Рис. 3. Зависимость безразмерного ускорения Г от наполнения полости q (m = 125 г, ν = 1 сСт) в пороге центрифугирования жидкости (1), возбуждения инерционных азимутальных волн (2), формирования рельефа (3) и обрушения центрифугированного слоя (4)
Фурье-анализ приведенных данных показывает, что колебания жидкости происходят с единственной частотой, близкой к скорости вращения цилиндра Ωosc ≈ 33.0 об/с (рис. 4б). Незначительное отклонение частоты осцилляций Ωosc от скорости вращения Ω связано с наличием осредненного азимутального течения, вследствие чего колебания жидкости происходят с частотой Ωosc = Ω + ΔΩ, здесь ΔΩ – скорость осредненного движения жидкости, при этом ΔΩ << Ω. Возникновение осредненного движения обусловлено волновыми процессами в жидкости. Согласно [5], при распространении волны элементы жидкости совершают такое незамкнутое орбитальное движение, что возникает средний дрейф в направлении распространения волны. Согласно наблюдениям азимутальная волна распространяется в сторону, противоположную вращению цилиндра, и скорость ΔΩ < 0.
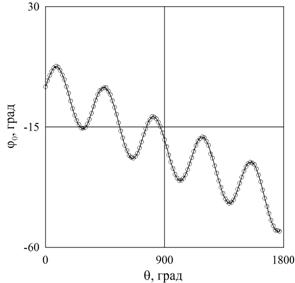 а
а
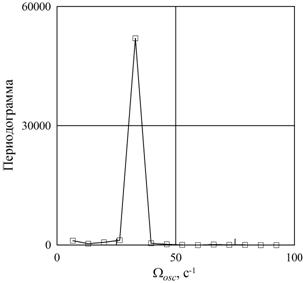 б
б
Рис. 4. Положение частицы вблизи центрифугированного слоя песка относительно вращающейся полости φ0 в зависимости от угла поворота полости θ (a) и результаты спектрального анализа (б): q = 0.182, Ω = 33.0 с-1, ν =2.9 сСт, m=125 г
Вычислим амплитудное значение скорости колебательного движения жидкости v0. Согласно рис. 4а амплитуда колебаний жидкости равна φmax = 0.17 рад, тогда амплитуда колебаний b = φmaxr. Расстояние r от центра полости до маркера, который движется вблизи песчаной подложки, можно вычислить по формуле r = D/2 – h, где h – толщина слоя песка. При массе песка m = 125 г толщина песчаной подложки равна 0.27 см. Следовательно, b = 1.02 см. Для амплитуды скорости азимутальных колебаний имеем v0 = bΩosc = 34 см/с.
Полученные экспериментальные данные можно сравнить с предсказаниями теории [4] для маловязкой жидкости в быстровращающемся бесконечно длинном горизонтальном цилиндре в поле силы тяжести. Согласно теории скорость вынужденных колебаний жидкости можно вычислить по формуле:
![]() , (2)
, (2)
здесь R – расстояние от центра полости до границы раздела между жидкостью и песком, g – ускорение свободного падения. В приведенном примере амплитудное значение скорости жидкости вблизи границы раздела равно v0 = 24 см/с. Таким образом, экспериментальные результаты измерения скорости колебаний жидкости удовлетворительно согласуются с теоретическими предсказаниями [4].
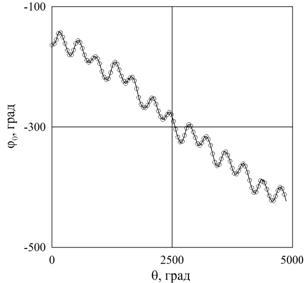 а
а
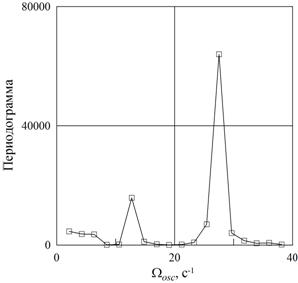 б
б
Рис. 5. Положение частицы вблизи центрифугированного слоя песка относительно вращающейся полости φ0 в зависимости от угла поворота полости θ (a) и результаты спектрального анализа (б): q = 0.129, Ω = 28.7 с-1, ν =2.8 сСт, m=250 г, k = 3
Если на поверхности жидкости возбуждаются бегущие азимутальные волны, то они также приводят жидкость в колебательное движение. При этом жидкость совершает одновременно вынужденные и волновые колебания. На рис. 5а приведена зависимость азимутальной координаты маркера во вращающейся системе отсчета от угла поворота цилиндра. Как и прежде, помимо колебательного движения жидкость совершает осредненное азимутальное движение. Важно отметить, что скорость такого движения значительно превышает скорость азимутального дрейфа в отсутствие волн: тангенс угла наклона графика на рис. 5а равен относительной скорости осредненного движения жидкости. Измерения показывают, что тангенс угла наклона равен 0.06, так что действительная скорость жидкости в лабораторной системе отсчета Ωl = 27.0 об/с.
Фурье-анализ показывает, что колебательное движение жидкости является суперпозицией двух гармонических колебаний (рис. 5б). Колебания с частотой Ωosc1 ≈ 27 с-1 происходят с частотой, равной скорости вращения жидкости Ωl. Второй пик соответствует частоте Ωosc2 = 13 с-1 и определяется фазовой скоростью волны. Действительно, частота осцилляций жидкости равна:
Ωosc2 = k(Ωl – Ωw), (3)
где k – азимутальное волновое число, Ωw – фазовая скорость волны в лабораторной системе отсчета. Согласно наблюдениям в приведенном случае Ωw = 22.1 об/с и k = 3. Таким образом, частота Ωosc2 = 14.7 с-1, что хорошо согласуется с результатами Фурье-анализа.
Заключение. Во вращающемся цилиндре, частично заполненном жидкостью и сыпучей средой, сила тяжести генерирует в жидкости азимутальные колебания, ответственные за появление квазистационарного рельефа в виде холмов, вытянутых вдоль оси вращения. Спектральный анализ показывает, что в общем случае колебательное движение жидкости представляет собой суперпозицию нескольких гармонических колебаний. Предложенная методика изучения колебательного движения позволяет изучить спектр колебаний жидкости и измерить скорость колебательного движения жидкости. Полученные результаты будут использованы для определения управляющих параметров в задаче об устойчивости границы раздела между жидкостью и сыпучей средой к появлению рельефа во вращающемся цилиндре.
Работа выполнена при финансовой поддержке Российского Научного Фонда (проект 14-11-00476)
Рецензенты:
Козлов В.Г., д.ф.-м.н., профессор, заведующий кафедрой общей и экспериментальной физики, ФГБОУ ВПО «Пермский государственный гуманитарно-педагогический университет», г. Пермь;
Иванова А.А., д.ф.-м.н., профессор, профессор кафедры общей и экспериментальной физики, ФГБОУ ВПО «Пермский государственный гуманитарно-педагогический университет», г. Пермь.
Библиографическая ссылка
Дьякова В.В., Полежаев Д.А. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ ЖИДКОСТИ В БЫСТРО ВРАЩАЮЩЕМСЯ ГОРИЗОНТАЛЬНОМ ЦИЛИНДРЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16199 (дата обращения: 23.02.2026).



