Одним из перспективных направлений современного приборостроения является использование оптических принципов измерения физических величин. Внедрение волоконно-оптических датчиков, по сравнению со стандартными электронными, позволяет значительно расширить диапазон и точность измерения. В одном из классов современных волоконно-оптических датчиков в качестве чувствительного элемента используется анизотропное одномодовое волокно сохраняющее состояние поляризации. Известны несколько вариантов конструкций подобного волокна: bow-tie, elliptical, pseudo-rectangle, elliptical core bow-tie, panda [6-8], которые отличаются между собой конструкцией, а именно формой и расположением силовых элементов, изготовленных из легированного кварцевого стекла. Одним из наиболее технологичных вариантов является оптическое волокно типа Panda, в котором два нагружающих элемента, имеющих цилиндрическую форму, изготовлены из кварцевого стекла, легированного оксидами бора и фосфора, и расположены по обе стороны от сердцевины. При высокотемпературной вытяжке волокна подобной конструкции, за счет неоднородности свойств материала по сечению заготовки, возникают остаточные напряжения, которые в силу известных фотоупругих эффектов влияют на оптические характеристики волокна.
При проектировании и моделировании волокна типа Panda предполагается, что сечения светопроводящей жилы, волокна и нагружающих стержней имеют круглую форму [4,5], центры светопроводящей жилы и волокна совпадают, а центры нагружающих элементов и светопроводящей жилы находятся на одной линии. Однако, вследствие несовершенства технологического процесса реальная геометрия изготавливаемого оптического волокна может существенно отличаться от проектной. В настоящей работе методами статистического анализа были обработаны данные по геометрии светопроводящей жилы. Полученные результаты использованы в численном эксперименте для определения влияния отклонений геометрии светопроводящей жилы от эталонных значений на напряженное состояние и на одну из ключевых оптических характеристик таких волокон - модовое двулучепреломление.
Статистический анализ экспериментальных данных
С помощью измерительной системы PK-2400 и программного пакета Matlab были получены значения геометрических параметров серии из 342 образцов анизотропных волокон типа Panda. В программном пакете STATISTICA определены математические ожидания и законы распределения экспериментальных данных.
Анализ результатов обработки фотоснимков поперечных сечений показал, что наиболее вероятная форма светопроводящей жилы является эллипсом, средние значения геометрических параметров которого и их распределения приведены в таблице 1 и на рис.1.
Таблица 1
|
|
Распределение |
Математическое ожидание, М |
Дисперсия, D |
|
Некруглость |
Бета |
0,108763 |
0,092323 |
|
Большой диаметр |
Логнормальное |
6,768359 мкМ |
0,154198 мкМ |
|
Малый диаметр |
Вейбулла |
6,059643 мкМ |
0,128481 мкМ |
Геометрические параметры светопроводящей жилы. Таблица 1.
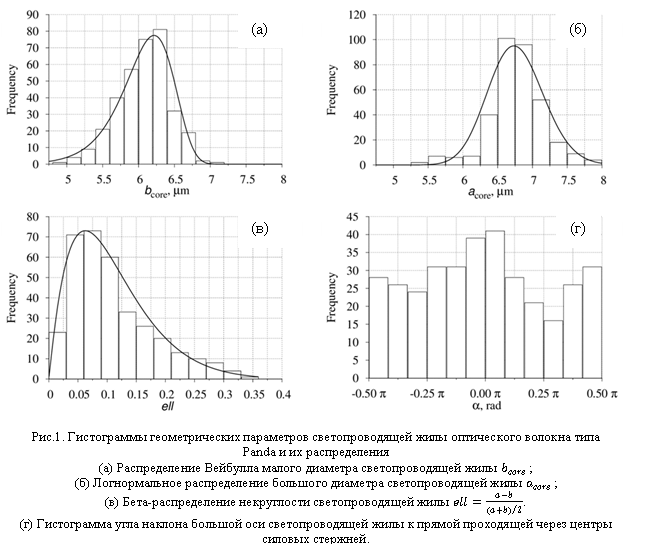
Полученные данные демонстрируют, что наиболее вероятная форма светопроводящей жилы значительно отличается от круга. Отклонения диаметров от проектного значения могут превышать 20%. Значения некруглости жилы достигают 0,385, а соответствующая ей эллиптичность 0,677. Кроме того, как показывают результаты измерений, такая эллиптичная жила может быть повернута к прямой, соединяющей центры силовых стержней. Данные по углу наклона α между большим диаметром светопроводящей жилы и прямой, проходящей через центры силовых стержней, требуют дополнительного анализа. Необходимо увеличить количество исследуемых образцов, т.к. существующая выборка не позволяет подобрать адекватного закона распределения, вероятнее всего оно равномерное по всему диапазону наблюдения [-π/2:π/2] (Рис.1.г).
Математическая модель
Для оценки влияния подобных несовершенств геометрии светопроводящей жилы на напряженно-деформированное состояние и оптические характеристики волокна проведена серия численных экспериментов на основе математической модели термомеханического поведения кварцевых стекол в широком диапазоне температур [4], включая релаксационный переход.
Учитывая, что при охлаждении оптического волокна после высокотемпературной вытяжки происходят в основном температурные деформации, которые в связи с малостью коэффициентов линейного температурного расширения невелики, была принята гипотеза малых деформаций. Известно, что релаксационные переходы не сопровождаются выделением или поглощением тепла [1]. Принимая во внимание отсутствие источников тепла в материале, малость деформаций и пренебрежимо малое диссипативное тепловыделение, можно разделить краевую задачу нестационарной теплопроводности и краевую задачу термомеханики о напряженно-деформированном состоянии. Предполагается также, что в волокне реализуются условия существования плоскодеформированного состояния. Известно, что при охлаждении волокна в процессе вытяжки температура на поверхности и в центре волокна отличаются незначительно [3], поэтому решение квазистатической краевой задачи об изменении полей напряжений было выполнено с учётом предположения об однородности температуры в поперечном сечении волокна и зависимости от времени, установленной в [3].
С учетом принятых гипотез несвязанная квазистатическая краевая задача механики при отсутствии вклада массовых сил включает в себя:
уравнения равновесия
,
геометрические соотношения:
.
граничные условия:
,
физические соотношения:
, 
, 
,
где t - время, nx и ny - направляющие косинусы внешней нормали к границе Γ,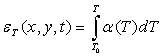 
- температурная деформация, 
, 
- компоненты тензора вязких деформаций
; 
- среднее напряжение, 
- единичный тензор второго ранга. Девиатор тензора вязкой деформации 
, в силу того, что в расплавленном состоянии материал предполагается несжимаемой жидкостью 
, равен тензору вязких деформаций 
; 
- объемная деформация. K - модуль объемного сжатия; G - модуль сдвига.
Вследствие неоднородного легирования силовых стержней коэффициент линейного температурного расширения α и вязкость η являются функциями концентраций легирующих элементов и координат
, 
,
где 
- энергия активации, R - универсальная газовая постоянная, 
– концентрация легирующих элементов. Известно [2], что влияние небольших степеней легирования кварцевого стекла на упругие характеристики незначительно.
Численная реализация и анализ результатов
Подход к численной реализация описанной математическая модели аналогичен изложенному авторами в работе [4]. В программном пакете Ansys построена конечно-элементная модель и проведена серия численных экспериментов, в результате которых были получены распределения полей остаточных напряжений в оптическом волокне типа Panda с учетом отклонений геометрии светопроводящей жилы от проектных значений. На рис.2 приведена типичная картина распределения нормальных напряжений 
и 
в поперечном сечении светопроводящей жилы волокна для двух крайних значений угла поворота большой оси α=0 и α=π/2 при максимальном зафиксированном в обработанной выборке значении некруглости ell=0,385. Видно, что для варианта угла поворота большой оси эллипса α=0 обеспечивается в среднем по сечению более высокий уровень разности нормальных напряжений (за счет относительно более близкого расположения силовых стержней), кроме того распределение напряжений более однородно (за счет размещения всей жилы в более узком диапазоне расстояний).
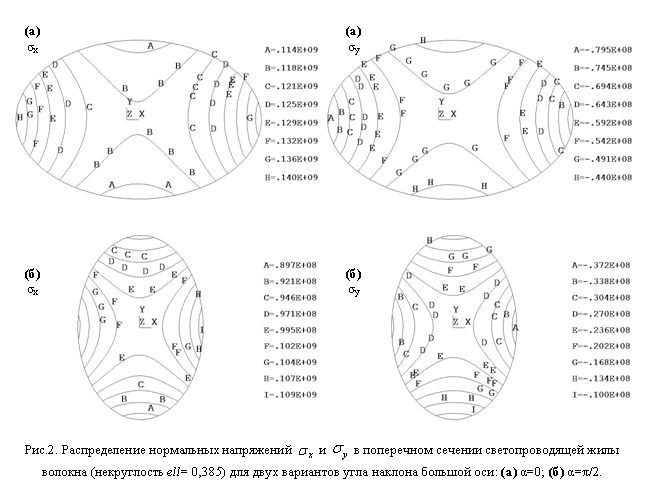
Анализ результатов численных экспериментов показал, что отклонения формы сечения светопроводящей жилы от проектной незначительно влияют на уровень напряженного состояния в волокне в целом. Разница между максимальными значениями интенсивностей напряжений при варьировании рассматриваемых отклонений геометрии жилы составила не более 2,5%. Однако, в области самой светопроводящей жилы картина распределения напряжений по сечению существенно меняется, что влечёт за собой изменение величины модового двулучепреломления B, которое вычисляется по формуле:
,
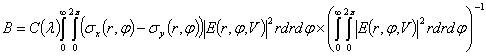где 
- соответствующие оси цилиндрической системы координат, 
и 
- нормальные напряжения в поперечном сечении волокна, 
- фотоупругая постоянная для данной длины волны, 
- распределение интенсивности основной моды по поперечному сечению световода, которое в данной работе принималось равномерным распределением 
в области светопроводящей жилы.
Обобщением численных расчетов являются зависимости, представленные на рис.3. Влияние на модовое двулучепреломление ориентации большой оси эллиптической жилы со значением некруглости равной 0,385 отражено на рис.3.а. Видно, что при фиксированном положении и размерах силовых стержней более благоприятное поле напряжений и, следовательно, большая величина модового двулучепреломления, реализуется в случае, когда угол α=0. Наиболее неблагоприятная ориентация соответствует углу α=π/2. Пунктирной линией на рис.3.а изображена зависимость модового двулучепреломления от угла поворота жилы при значении некруглости ell=0, т.е. сечение жилы имеет проектную, круглую форму. Как и ожидалось в случае симметричной круглой жилы от угла ее поворота ничего не меняется. Все остальные зависимости двулучепреломления от угла для прочих значений некруглости в диапазоне [0:0,385] , расположены между этими графиками, и пересекаются в точке α=π/4.
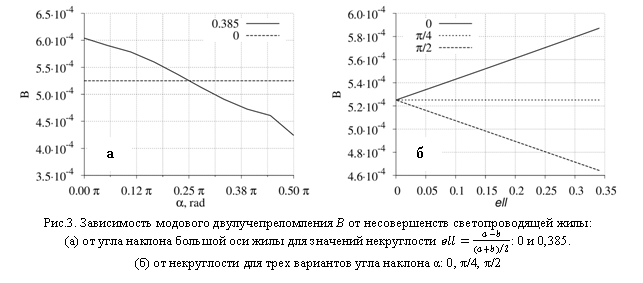
Рис.3.б демонстрирует влияние на двулучепреломление степени эллиптичности жилы для трех случаев ориентации большой оси эллиптического сечения α=0, α=π/4 и α=π/2. В расчетах учитывалось, что изменение эллиптичности жилы не сопровождается изменением площади ее поперечного сечения. Видно, что при фиксированном положении и размерах силовых стержней в случае, когда угол α=0, увеличение эллиптичности жилы ведет к увеличению двулучепреломления. Это происходит за счет уменьшения зазора между силовыми стержнями и жилой при увеличении размера большой оси эллипса (увеличения уровня напряжений) и, одновременно, за счет более однородного распределения напряжений вследствие размещения всей жилы в более узком диапазоне расстояний. Наоборот, в случае, когда угол α=π/2, увеличение эллиптичности жилы ведет к уменьшению двулучепреломления. Кроме того, как видно из рис.3.б, при α=π/4 модовое двулучепреломление не зависит от значений некруглости в исследованном диапазоне [0:0,35] при фиксированном положении и размерах силовых стержней.
Заключение
Таким образом, исследовано влияние некруглости и ориентации светопроводящей жилы на величину модового двулучепреломления световода типа Panda. Установлено, что для заданной некруглости сердцевины при фиксированном положении и размерах силовых стержней большее двулучепреломление реализуется в случае, когда ориентация большой оси эллипса совпадает с направлением расположения силовых стержней, а минимальное двулучепреломление соответствует ориентации большой оси перпендикулярно к прямой, соединяющей центры силовых стержней. При фиксированном положении и размерах силовых стержней в случае, когда угол α=0, увеличение эллиптичности жилы ведет к увеличению двулучепреломления. Наоборот, в случае, когда угол α=π/2, увеличение эллиптичности жилы ведет к уменьшению двулучепреломления.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, гранта РФФИ проект № 13-08-96036 р_урал_а и 14-08-31530 мол_а.
Рецензенты:
Домбровский И.В., д.т.н., доцент, директор ЗАО «Специальное конструкторское бюро» ОАО «Мотовилихинские заводы», г. Пермь;
Шардаков И.Н., д.ф-м.н., профессор, заведующий лабораторией Института механики сплошных сред Уральского отделения Академии наук, г. Пермь.
Библиографическая ссылка
Труфанов А.Н., Труфанов Н.А., Семенов Н.В., Стрелкова Н.М. ВЛИЯНИЕ ТЕХНОЛОГИЧЕСКИХ НЕСОВЕРШЕНСТВ ФОРМЫ СВЕТОПРОВОДЯЩЕЙ ЖИЛЫ НА НАПРЯЖЕННОЕ СОСТОЯНИЕ И ОПТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОПТОВОЛОКНА ТИПА PANDA // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16198 (дата обращения: 20.04.2024).