В данной работе представлены результаты первого этапа исследований по созданию полной математической модели процессов термо-газодинамики и тепло-массообмена на поверхности гиперзвукового летательного аппарата (ГЛА) при полёте в атмосфере на высотах, удовлетворяющих по параметрам модели сплошной среды. Представленные результаты были получены с помощью математической модели, которая подробно описана в работе [2].
Актуальность работы обусловлена тем, что одной из важнейших проблем при проектировании ГЛА является достоверное предсказание параметров тепло-массообмена на его поверхности. Правильное решение этой задачи позволяет уже на стадии проектирования перспективного аппарата оптимизировать его геометрические, траекторные, весовые и прочие параметры, а также определить потребную толщину и материалы в составе тепловой защиты летательного аппарата.
1. Постановка задачи.
В работе исследовались процессы термо-газодинамики и теплообмена при обтекании гиперзвуковым потоком сферы радиусом R0= 0,03048 м, выполненной из графита с покрытием и без покрытия. Скорость набегающего потока соответствовала числу Маха, М = 29,45. Статические параметры состояния газа в потоке: температура – 196,7 К, давление – 12,21 Па.
Задача решалась в строгой постановке с применением сеточных методов численного моделирования. Расчёт теплообмена на поверхности сферы проводился с учётом каталитической активности поверхности. Рассматривались два предельных случая. В первом, графитовая поверхность сферы принималась абсолютно каталитической (кw → ∞). Во втором, на поверхности сферы формировалось покрытие, обладающее нулевой каталитической активностью (кw → 0). В том и другом случае поверхность сферы принималась химически нейтральной к компонентам набегающего потока, т.е. поверхность сферы считалась непроницаемой.
В научной печати опубликован ряд работ, в которых исследовались процессы термо-газодинамики и теплообмена при обтекании сфер разных диаметров в широком диапазоне изменения чисел Маха набегающего потока с помощью различных методов. Результаты, полученные с помощью выше упомянутой методики, сравнивались с данными работ [4] и [5].
2. Анализ результатов расчёта с использованием неадаптированных и адаптированных расчётных сеток.
На рисунке 2.1. приведена цветовая гамма поля обезразмеренной статической температуры в сжатом и пограничном слое, полученная с использованием исходной расчётной сетки, а также двух более мелких сеток, которые были получены из исходной путём последовательной адаптации. Расчёт выполнен для поверхности сферы, обладающей абсолютной каталитической активностью.
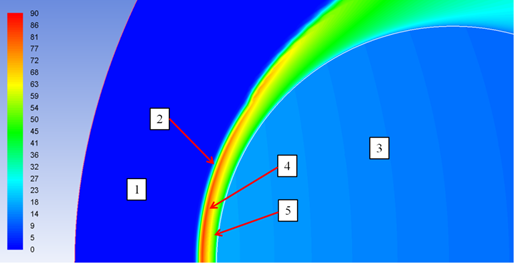
а) результаты расчёта на исходной сетке.
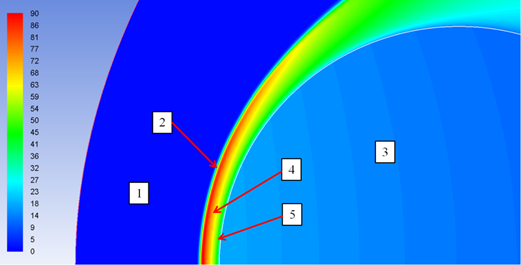
б) результаты расчёта после адаптации №1
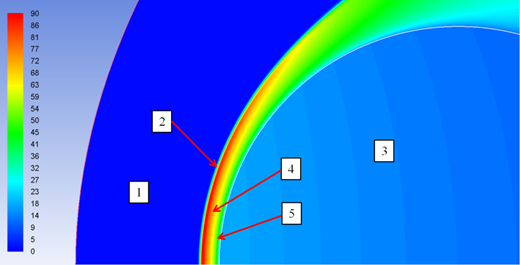
в) результаты расчёта после адаптации №2
Рис. 2.1. Поле безразмерной статической температуры, ![]() .
.
1- невозмущённый поток, 2- ударная волна, 3- обтекаемое тело, 4 - сжатый слой,5- пограничный слой.
Покажем, что адаптация расчётной сетки приводит к уточнению как положения и формы головного скачка уплотнения (отошедшей ударной волны), так и его термодинамических свойств.
На
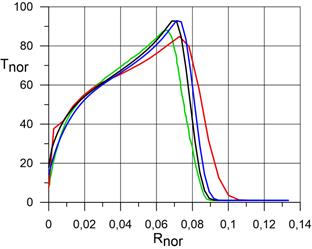
рисунке 2.2 представлены результаты расчёта распределения безразмерной
статической температуры ![]() , безразмерной
плотности
, безразмерной
плотности ![]() и безразмерного давления
и безразмерного давления ![]() по нормали к поверхности сферы в точке
торможения, полученные с использованием трёх описанных выше расчётных сеток
(исходной и двух адаптированных). По оси абсцисс отложен безразмерный радиус
сферы
по нормали к поверхности сферы в точке
торможения, полученные с использованием трёх описанных выше расчётных сеток
(исходной и двух адаптированных). По оси абсцисс отложен безразмерный радиус
сферы ![]() .
.
Из представленных данных следует, что положение головного скачка уплотнения и его термодинамических параметров сильно разнятся при использовании неадаптированной и адаптированных расчётных сеток. Это объясняется тем, что при использовании адаптированных расчётных сеток более достоверно определяются градиенты газодинамических параметров с применением более мелких ячеек.
Полученные данные расчёта показали также, что адаптация /2/ влияет на указанные параметры гораздо слабее, хотя её структура включает значительно большее количества расчётных ячеек.
|
|
|
|
a) распределение Tnor; |
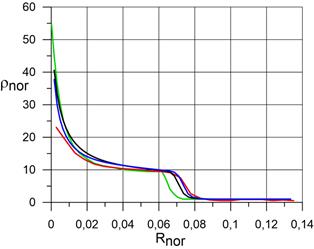
б) распределение ρnor; |
|
|
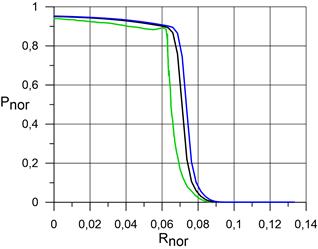
Рис. 2.2. Распределение безразмерной температуры, безразмерной плотности и безразмерного давления в сжатом и пограничном слое по нормали к поверхности сферы в точке торможения. На рисунке: координаты от 0 (поверхность сферы) до 0,07 – пограничный и сжатый слой.
|
|
в) распределение Pnor; |
|
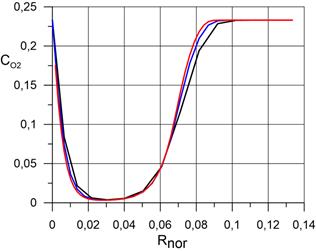
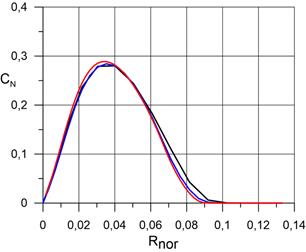
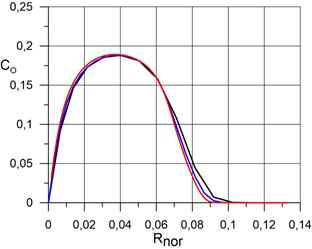
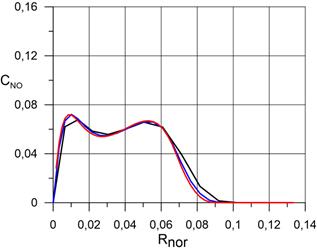
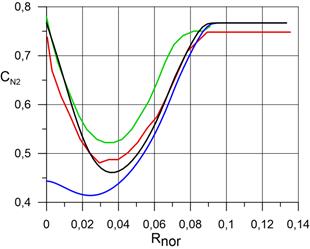
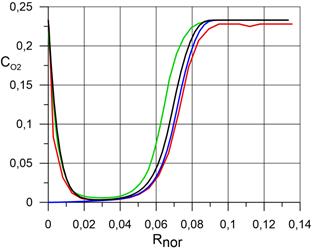
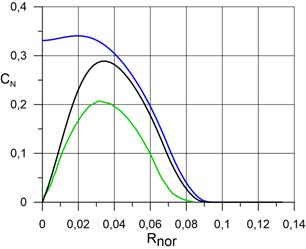
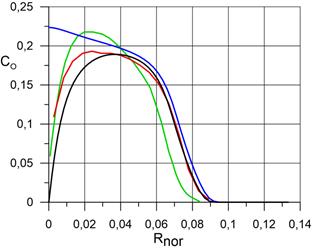
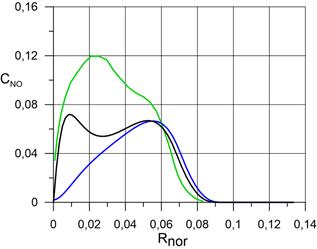
На рисунке 2.3 представлены распределения массовых концентраций компонентов N2, O2, N, O, NO, в сжатом и пограничном слое по нормали к поверхности сферы в точке торможения при использовании трёх расчётных сеток, соответственно. Расчёт проведён для случая абсолютной каталитической активности поверхности сферы. Видно, что последующая адаптация расчётной сетки не оказывает значительного влияния на распределения компонентов.
Таким образом, по результатам приведённого анализа принято решение применять в расчётах адаптированную сетку. Ниже представлены результаты расчётов с использованием такой сетки.
|
|
|
|
a) распределение N2; |
б) распределение O2; |
|
|
|
|
в) распределение N; |
г) распределение O; |
|
|
Рис. 2.3. Распределение массовых концентраций N2, O2, N, O, NO в сжатом и пограничном слое по нормали к поверхности сферы в точке торможения. На рисунке координаты от 0 (поверхность сферы) до 0,07 – пограничный и сжатый слой.
|
|
д) распределение NO; |
|
3. Анализ результатов верификации предложенной математической модели.
Как отмечалось, расчёт математической модели проведён численным методом для двух предельных случаев: на абсолютно каталитической поверхности сферы и на некаталитической поверхности. Следует отметить, что в работах [4], [5] исследования проведены только для одного предельного случая – для абсолютно каталитической поверхности.
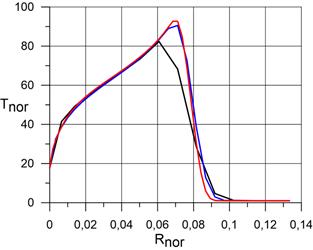
На рисунке 3.1 представлены распределения безразмерной статической температуры, безразмерной плотности и безразмерного давления по нормали к поверхности сферы в точке торможения в сравнении с данными работ [4], [5].
Результаты представлены для случаев абсолютно каталитической поверхности сферы и некаталитической поверхности.
Сопоставление показало, что данные хорошо согласуются в плане положения головного скачка уплотнения, а также в плане параметров набегающего потока на поверхности сферы. Однако наблюдается некоторое завышение максимальной статической температуры в скачке уплотнения (на 4% по сравнению с результатами работы [4] и на 8% по сравнению с результатами работы [5]).
|
|
|
|
a) распределение Tnor; |
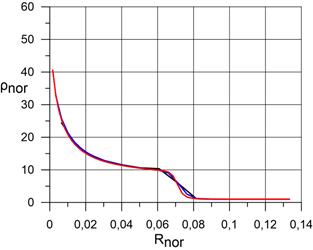
б) распределение ρnor; |
|
|
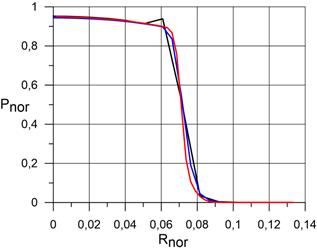
Рис. 3.1. Сравнение результатов расчёта распределения по нормали к поверхности сферы в точке торможения безразмерной температуры, безразмерной плотности и безразмерного давления в сжатом и пограничном слое. На рисунке: координаты от 0 (поверхность сферы) до 0,07 – пограничный и сжатый слой. |
|
в) распределение Pnor; |
|
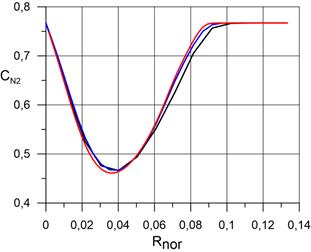
На рисунках 3.2 представлены распределения массовых концентраций компонентов N2, O2, N, O, NO, по нормали к поверхности сферы в точке торможения в сравнении с данными статей [4], [5]. Как и прежде, расчёт проведён для случаев абсолютно каталитической поверхности сферы и некаталитической поверхности. Видно, что результаты, полученные для абсолютно каталитической поверхности сферы удовлетворительно согласуются данными работ [4] и [5]. Существенные расхождения наблюдаются для тех компонентов, концентрация которых мала: N, NO. Для атомарного азота результаты оказались завышены на 38% по сравнению с работой [4]. Для оксида азота результаты оказались завышены на 70% по сравнению с работой [4]. Кроме того для оксида азота наблюдаются качественные различия в распределении концентрации по оси OX, чего не наблюдается для других компонентов. По-видимому единственная причина столь больших расхождений обусловлена большой численной жесткостью уравнений химической кинетики скорости образования указанных компонентов, которая приводит к неправильному определению их концентраций.
|
|
|
|
a) распределение N2; |
б) распределение O2; |
|
|
|
|
в) распределение N; |
г) распределение O; |
|
|
Рис. 3.2. Сравнение результатов расчёта распределения по нормали к поверхности сферы в точке торможения массовых концентрацийN2, O2, N, O, NO в сжатом и пограничном слое. На рисунке: координаты от 0 (поверхность сферы) до 0,07 – пограничный и сжатый слой. |
|
д) распределение NO; |
|
Следует заметить, что в том случае, когда поверхность сферы обладает абсолютной каталитической активностью, концентрации всех компонентов вблизи поверхности принимают свои значения в невозмущённом потоке. В случае, когда поверхность сферы принимается некаталитической, реакции рекомбинации не проходят и сфера обтекается главным образом потоком атомарного кислорода и азота, что вполне реально.
Приведённые в работе исследования дают возможность в рамках сформулированной задачив дальнейшем провести расчёт тепло- и массообмена на повехности сферы и других геометрических форм. По результатам полученных данных будет проведено сопоставление параметров тепло-массообмена в передней критической точке с результатами расчёта задачи, полученными с использованием алгебраических критериальных соотношений, которые подробно описаны в работах [1] и [3]. Результаты будут также опубликованы в данном журнале.
Выводы
1. Проведены и проанализированы результаты численного моделирования процессов термо-газодинамики, протекающих на поверхности сферы при её обтекании гиперзвуковым потоком. Расчёты представлены для двух предельных случаев: абсолютно каталитическая и некаталитическая поверхность. Показано, что полученные данные по координатному расположению головной ударной волны, а также распределений безразмерных статической температуры и статического давления и безразмерной плотности по нормали к поверхности сферы в точке торможения удовлетворительно согласуются с результатами работ [4] и [5].
2. Получено удовлетворительная корреляция результатов распределения массовых концентраций компонентов O2, N2, O по нормали к поверхности сферы в точке торможения с результатами работ [4] и [5]. Однако наблюдаются значительное несоответствие в распределении атомарного азота N и оксида азота NO по сравнению с данными работы [4]. Это отличие, вероятно, обусловлено большой численной жесткостью уравнений переноса для этих компонентов и требует дальнейшего изучения.
3. Представленная математическая модель отличается от моделей [4] и [5] тем, что в них авторы представляли воздух как семикомпонентную реагирующую смесь. В расчётах присутствовала реакция образования иона NO+ и выделения свободных электронов. Однако в ходе предварительных исследований было установлено, что скорость этой реакции практически равна нулю. В настоящее время вопрос целесообразности учёта этой реакции требует дальнейшего изучения.
4. Полученные результаты численных расчётов представленной математической модели и результаты её верификации указывают на то, что разработанная математическая модель может быть использована при решении термо-газодинамических и теплотехнических задач при проектировании теплонапряженных элементов конструкции гиперзвуковых ЛА.
Работа выполнена при поддержке РФФИ, грант № 13-08-01328 а.
Рецензенты:
Молчанов А.М., д.т.н., доцент Московского авиационного института (национального исследовательского университета), г. Москва;
Тимушев С.Ф., д.т.н., профессор Московского авиационного института (национального исследовательского университета), г. Москва.
Библиографическая ссылка
Быков Л.В., Никитин П.В., Пашков О.А. АНАЛИЗ РЕЗУЛЬТАТОВ ВЕРИФИКАЦИИ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ТЕРМО-ГАЗОДИНАМИКИ И ТЕПЛО-МАССООБМЕНА ПРИ ОБТЕКАНИИ СФЕРЫ ВОЗДУШНЫМ ГИПЕРЗВУКОВЫМ ПОТОКОМ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16138 (дата обращения: 23.02.2026).