Реальные временные ряды экономических показателей (котировок акций, курсов валют, показателей финансовой отчетности предприятий) демонстрируют сложное непериодическое поведение, при котором тренды и флэты хаотическим образом сменяют «броуновское» движение. Развитие и прогнозирование таких рядов эффективно описывать методами фрактальной параметризации. Для большинства естественных временных рядов аналитическое нахождение фрактальной размерности невозможно, поэтому D определяют численно: либо непосредственно, либо через величины, связанные с ней простым соотношением (например, через показатель Херста H). Непосредственное определение фрактальной размерности чаще всего проводят используя один из двух методов – метод клеточного покрытия временного ряда либо метод минимального покрытия. Следует отметить, что существуют и менее распространенные методы определения фрактальной размерности, например через корреляционный интеграл с помощью алгоритма Грассберга-Прокаччи [5].
В настоящей работе для реальных временных рядов экономических показателей сравниваются несколько наиболее распространенных методов определения фрактальных характеристик, которые позволяют сделать выводы о данном распределении и прогнозировать дальнейшее поведение временного ряда.
Методология
Определение фрактальной размерности методом
клеточного покрытия временного ряда. Суть клеточного метода основано
на соотношении, введенном Хаусдорфом, как знаменитое определение размерности D для
компактного множества в произвольном метрическом пространстве: ![]() (1)
(1)
Пусть на отрезке [a,b]
задана функция ![]() , имеющая не более конечного числа точек
разрыва первого рода: именно такие функции естественно рассматривать в качестве
модельных, например для финансовых временных рядов. Вводится равномерное
разбиение отрезка
, имеющая не более конечного числа точек
разрыва первого рода: именно такие функции естественно рассматривать в качестве
модельных, например для финансовых временных рядов. Вводится равномерное
разбиение отрезка
![]() , (2),
, (2),
где ![]() (
(![]() ).
).
Если подобные множества покрывать носителями (в частности,
клетками) с размером ![]() , то с уменьшением
, то с уменьшением ![]() количество клеток N будет расти по степенному закону:
количество клеток N будет расти по степенному закону:
![]() , (3)
, (3)
где D – фрактальная размерность.
При
логарифмировании получаем классическое определение хаусдорфовской фрактальной
размерности (1). Для определения размерности D по методу клеток, плоскость, на которой
определен график временного ряда, разбивается на клетки размером ![]() и
определяется число клеток N(
и
определяется число клеток N(![]() )
, где находится хотя бы одна точка этого графика. Затем меняется
)
, где находится хотя бы одна точка этого графика. Затем меняется ![]() и
в двойном логарифмическом масштабе строится график функции N(
и
в двойном логарифмическом масштабе строится график функции N(![]() ), который аппроксимируется прямой с
помощью метода наименьших квадратов (МНК). Тогда D определяется по углу наклона этой прямой.
), который аппроксимируется прямой с
помощью метода наименьших квадратов (МНК). Тогда D определяется по углу наклона этой прямой.
Определение фрактальной
размерности методом минимального покрытия временного ряда. Метод
минимального покрытия, детально разработанный в трудах [1,7] позволяет
характеризовать локальную динамику процесса. Для этого сужается репрезентативный
масштаб до значений, где временной ряд не меняет своего поведения,
определяется локальная фрактальная размерность (авторы называют ее размерность
минимального покрытия). Чтобы связать локальную
динамику соответствующего процесса с фрактальной размерностью временного ряда
необходимо определить размерность D локально. Для этого находится
последовательность аппроксимаций, которая при фиксированном ![]() была бы в некотором
смысле оптимальной. Для площади аппроксимаций
была бы в некотором
смысле оптимальной. Для площади аппроксимаций
![]() :
:
![]() при
при ![]() (4)
(4)
Действительно,
для той же функции ![]() график покрывается прямоугольниками таким
образом, чтобы это покрытие было минимальным по площади в классе покрытий прямоугольниками
с основанием
график покрывается прямоугольниками таким
образом, чтобы это покрытие было минимальным по площади в классе покрытий прямоугольниками
с основанием ![]() . Тогда высота прямоугольника на отрезке
. Тогда высота прямоугольника на отрезке ![]() будет равна амплитуде
будет равна амплитуде ![]() , которая является разностью между
максимальным и минимальным значением функции
, которая является разностью между
максимальным и минимальным значением функции ![]() на
этом отрезке.
на
этом отрезке.
Вводится величина![]() , названная индексом фрактальности и связанная с фрактальной размерностью соотношением
, названная индексом фрактальности и связанная с фрактальной размерностью соотношением![]() . При этом, размерность
. При этом, размерность
![]() называется размерностью минимального покрытия.
В этой же работе показано, что для реальных фрактальных функций минимальные и
клеточные покрытия близки, хотя и могут давать различные приближения величины
называется размерностью минимального покрытия.
В этой же работе показано, что для реальных фрактальных функций минимальные и
клеточные покрытия близки, хотя и могут давать различные приближения величины ![]() к асимптотическому режиму.
к асимптотическому режиму.
Показано, что эта функция является индикатором локальной
стабильности временного ряда: чем больше значение ![]() , тем
стабильнее ряд.
, тем
стабильнее ряд.
Метод R/S анализа временных рядов и определение показателя Херста
Для калибровки временных измерений Херст ввел безразмерное отношение посредством деления размаха на стандартное отклонение наблюдений R/S. Этот способ анализа стали называть методом нормированного размаха, или R/S-анализом [6] .R/S-анализ является процессом , который требует переработки большого количества данных.
Как известно,
показатель Херста H определяется
на основе предположения, что усредненный по времени модуль разности значений функции
![]() связан
с
связан
с ![]() :
:
![]() при
при ![]() , (5)
, (5)
Как уже
отмечалось, если ![]() реализация
гауссовского случайного процесса, то показатель H связан с размерностью D,
а следовательно и с индексом
реализация
гауссовского случайного процесса, то показатель H связан с размерностью D,
а следовательно и с индексом ![]() , соотношением:
, соотношением:
![]() (6)
(6)
Как указывается в [7], индекс ![]() вычисляется на порядок более точно, чем
показатель Херста H в подавляющем
большинстве случаев.
вычисляется на порядок более точно, чем
показатель Херста H в подавляющем
большинстве случаев.
Результаты
Значение фрактальных показателей D, H и ![]() соотносится
со сложным непериодическим поведением реальных
временных рядов, при котором тренды и флэты хаотическим образом сменяют стохастическое
движение, и прогнозировать дальнейшее поведение временного ряда. Сопоставление
фрактальных показателей при обработки временных рядов, проведенное в работах
разных научных коллективов, позволяет нам представить их взаимосвязь при
определении тенденций ряда следующим способом.
соотносится
со сложным непериодическим поведением реальных
временных рядов, при котором тренды и флэты хаотическим образом сменяют стохастическое
движение, и прогнозировать дальнейшее поведение временного ряда. Сопоставление
фрактальных показателей при обработки временных рядов, проведенное в работах
разных научных коллективов, позволяет нам представить их взаимосвязь при
определении тенденций ряда следующим способом.
Таблица 1
Сравнение фрактальных характеристик временных рядов
|
Показатели фрактальности |
Характер временного ряда экономического показателя |
||
|
Антиперсистентный (возврат к среднему [6], флэт [7]) |
Случайный (стохастический, винеровский шум, промежуточное состояние [7]) |
Персистентный (трендоустойчивый [6], Тренд [7]) |
|
|
Показатель Херста H |
0 < H<0,5 |
H =0,5 |
0,5 < H<1 |
|
Фрактальная размерность D |
2 > D >1,5 |
D =1,5 |
1,5 > D >1 |
|
Индекс фрактальности |
1 > |
|
0,5 > |
Из таблицы видно, что все три показателя, согласуются друг с другом при определении характера временного ряда экономических показателей.
Так, при 1,5 > D >1 временные ряды (валютных курсов, курсов акций и др.) имеют долговременную корреляцию, возникает персистентное состояние рынка, полностью характеризующееся показателем фрактальной размерности. В этом случае количественный математический анализ имеет большую достоверность, что позволяет прогнозировать текущую экономическую обстановку именно с помощью классических методов анализа. Причем, близкое к единице значение фрактальной размерности указывает на скорое окончание действующего тренда. При D =1,5 с разбросом ± 0,05 поведение системы стохастическое и хорошо описывается классическими статистическими методами, т.е. распределение курсов акций рынке является гауссовским лишь при значении фрактальной размерности в узком интервале. При 2 > D >1,5, чем ближе D к двойке, тем более нелинейным становится временной ряд , возникает антиперсистентное состояние курса акций, временная кривая курса становится неустойчивой и готова перейти в новое состояние. При таком диапазоне фрактальной размерности остается лишь использовать анализ фундаментальных факторов состояния экономики.
Индекс фрактальности ![]() также
является показателем стабильности исходного временного ряда: чем больше
значение
также
является показателем стабильности исходного временного ряда: чем больше
значение ![]() , тем стабильнее поведение ряда и чем
меньше
, тем стабильнее поведение ряда и чем
меньше ![]() , тем сильнее в исходном ряде выражен
тренд, иначе говоря, случай
, тем сильнее в исходном ряде выражен
тренд, иначе говоря, случай ![]() <0,5 естественно
интерпретировать как тренд, а случай
<0,5 естественно
интерпретировать как тренд, а случай ![]() >0,5 - как флэт.
>0,5 - как флэт.
Проведем сравнительную оценку точности показателей фрактальности – индекса Херста и фрактальной размерности на примере ряда акций компании Лукойл (LHOL на ММВБ) и покажем, что наиболее точно фрактальная размерность определяется не через показатель Херста, а методом покрытия – клеточного или минимального. Выберем временной ряд котировок акций за 1999 год – относительно спокойный докризисный период. В десятилетнем временном промежутке котировок акций с 1999 по 2009 годы этот участок может рассматриваться как устойчивый тренд с небольшой тенденцией на повышение – персистентный ряд, как показано на рис.1.
 а
а
 б
б
Рис.1. Временной ряд котировок акций Лукойл на ММВБ по данным BFM cervice
а ) ряд котировок за десятилетний период 1999-2009;
б ) укрупненно анализируемый участок этого ряда за 1999 г.
Для
этого годового ряда котировок на рис.2 приведен результат определения фрактальной
размерности методом клеточного покрытия временного ряда, по соотношениям (1)
–(3) при МНК аппроксимации зависимости lnN(![]() )-ln(
)-ln(![]() ). Более подробно алгоритм
описан в работах [2-4].
). Более подробно алгоритм
описан в работах [2-4].
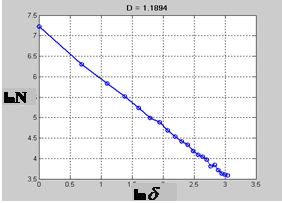
Рис.2. МНК-аппроксимация зависимости фрактальной меры от размерного фактора и определение фрактальной размерности D методом клеточного покрытия временного ряда котировок акций Лукойл, приведенного на рис 1(б).
Фрактальная размерность ряда D = 1,18, что свидетельствует о его персистентном трендоустойчивом характере. Близкое к единице значение фрактальной размерности указывает на скорое окончание действующего тренда, что и произошло в 2000-2001 годах.
На рис. 3 показана лог-лог диаграмма для численного определения показателя Херста по тому же отрезку финансового временного ряда с использованием формул (5). Показатель Херста ряда равен Н=0,40. Обращаем внимание на невысокий коэффициент детерминации R = 0,56 при уровне надежности 0,95. Определенная из соотношения (6) по показателю Херста фрактальная размерность равна D = 1,51, что свидетельствует о случайном поведении ряда с высоким уровнем стохастичности. В то же время, временной период 1999 года для котировок акций Лукойл едва ли можно отнести к таковым.
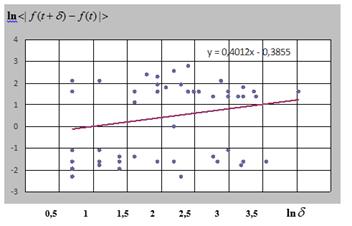
Рис.3. Лог-лог диаграмма для численного определения показателя Херста по тому же отрезку финансового временного ряда котировок акций Лукойл, приведенного на рис 1б.
Таким образом, наиболее корректно для оценки и прогнозирования временного ряда таких показателей макроэкономики, как котировки акций, применять фрактальную размерность, определенную методом покрытия, в нашем случае клеточного.
В наших работах [2-4] с помощью этого метода определения фрактальной размерности исследованы ценовые ряды акций компании Лукойл 1999 и 2009 г.г., а также ряды микроэкономических показателей для ряда предприятий сервиса нефтеобработки Приволжского Федерального Округа. Анализ проводился по временному интервалу от годового до десятилетнего, каждый ряд содержал от пятисот значений. Для уточнения и сравнительного анализа, кроме периодов 1999 г. и 2009 г., соответствующих докризисному и послекризисному поведению временных рядов, рассматривали также период кризиса 2008 г. Установлено, что экономический кризис приводит к усилению фрактальных свойств временных рядов как макроэкономических показателей (более подробно для ряда акций LHOL на ММВБ в работе [4]), так и рядов показателей финансовой отчетности региональных предприятий ПФО [3]. Для периодов активного развития кризиса и в предкризисные годы наиболее существенным является не абсолютное значение фрактальной размерности, а ее относительное изменение более чем на 10% в течение годового периода – это является своеобразным «флагом» катастрофы.
Выводы
1.
Сопоставление фрактальных характеристик при обработки временных рядов экономических
показателей - фрактальной размерности D, индекса фрактальности ![]() и показателя
Херста H -
показывает, что они согласуются друг с другом при определении характера
временного ряда, но отличаются точностью.
и показателя
Херста H -
показывает, что они согласуются друг с другом при определении характера
временного ряда, но отличаются точностью.
2. Проведена сравнительная оценка точности показателей фрактальности – индекса Херста и фрактальной размерности на примере ряда акций компании Лукойл (LHOL на ММВБ). Установлено, что наиболее точно фрактальная размерность определяется не через показатель Херста, а методом клеточного покрытия.
3. Выявлена связь фрактальной размерности D с динамикой, уровнем и состоянием рынка ценных бумаг на примере макроэкономического показателя – котировок акций LHOL на ММВБ. Установлено, что экономический кризис приводит к усилению фрактальных свойств временных рядов экономических показателей.
Рецензенты:
Ёлохова И.В.., д.э.н., зав. каф. «Экономика и финансы» ПНИПУ, г. Пермь.
Беленький В.Я., д.т.н., проф., декан МТФ ПНИПУ, г. Пермь.
Библиографическая ссылка
Кривоносова Е.К., Первадчук В.П., Кривоносова Е.А. СРАВНЕНИЕ ФРАКТАЛЬНЫХ ХАРАКТЕРИСТИК ВРЕМЕННЫХ РЯДОВ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15974 (дата обращения: 12.03.2026).



