При диагностике и контроле методом вихревых токов в проводящем объекте индуцируют вихревые токи с помощью индуктивных датчиков. Появление дефектов в зоне контроля или изменение расстояния между датчиком и проводящей поверхностью образца отражаются на информативных характеристиках накладного измерительного преобразователя. Для параметрического датчика регистрируют изменение его импеданса на различных частотах [6]. Графически влияние параметров проводящих объектов и режимов измерений на характеристики вихретокового преобразователя представляют на комплексной плоскости в виде годографов. При низкой точности измерений использование методов контроля, основанных на анализе годографов вихретоковых преобразователей, может оказаться неэффективным [1; 2]. В настоящей работе разработано микропроцессорное устройство, позволяющее в автономном режиме получать годографы вихретокового преобразователя и контролировать толщину диэлектрических покрытий на основе алюминиевых сплавов.
Описание разработанной экспериментальной установки и метода расчета
Структурная схема разработанного вихретокового устройства приведено на рис. 1.
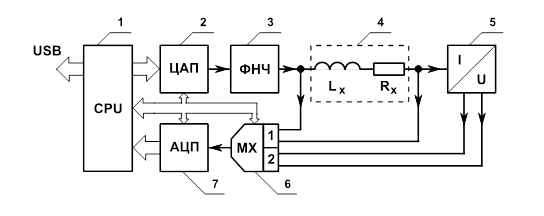
Рис. 1. Структурная схема вихретокового устройства.
На микроконтроллере 1 и цифроаналоговом преобразователе 2 и фильтре низкой частоты 3 был собран синусоидальный генератор прямого цифрового синтеза. Сформированный сигнал пропускался через параметрический вихретоковой датчик 4. Для регистрации силы тока применяли преобразователь «ток - напряжение» 5. Мультиплексор 6 последовательно подключал ко входу АЦП сигналы с первого и второго каналов, мгновенные значения которых передавались в микроконтроллер для дальнейшей обработки. Созданная программа рассчитывала комплексные амплитуды напряжения на датчике и силы тока, протекающего через него.
Для генерации синусоидального сигнала использовался цифро-аналоговый преобразователь, содержащий таблицу синусов. Такое решение позволило генерировать сигнал в широком диапазоне частот без использования расчетных таблиц и дополнительных расчетов в реальном времени. Осциллограмма сигнала, полученная с помощью цифрового осциллографа ACK-2062, приведена на рис. 2а. На рис. 2б приведен спектр этого сигнала, полученный путем применения быстрого преобразования Фурье. Амплитуды гармоник приведены в логарифмическом масштабе. Как видно из рис. 2а, в спектре сигнала отчетливо выделяются 15 и 17 гармоники.
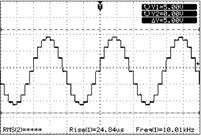
а) б)
Рис. 2: а) сигнал на выходе цифро-аналогового преобразователя; б) спектр сигнала.
Для уменьшения уровня высших гармоник применяли программируемый фильтр низких частот с регулируемой частотой среза. Он обеспечивал получение синусоидального сигнала с низким уровнем гармоник во всем частотном диапазоне, который применялся при измерениях. Для примера на рис. 3 приведены осциллограмма сигнала частотой 10 кГц и его спектр на выходе фильтра низкой частоты.
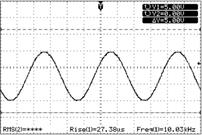
а) б)
Рис. 3: а) сигнал на выходе фильтра низких частот; б) спектр сигнала.
Применение микроконтроллера позволило применить цифровую обработку сигналов [5], показавшую свою эффективность при подавлении случайной помехи в различных устройствах обработки данных [2; 3]. Для определения комплексных амплитуд дискретные значения сигнала аппроксимировали линейной комбинацией трех первых функций Уолша [4] с весовыми коэффициентами 
, 
и 
:
,
где x = t/T - относительное время, Т - период сигнала. Такой ряд очень грубо описывает гармонический сигнал, но его коэффициенты содержат всю необходимую информацию об определяемых параметрах.
Коэффициенты b0, b1 и b2 определяли методом наименьших квадратов по массиву дискретных данных 
, который содержал 
элементов. В этом случае целевая функция имела вид:
.
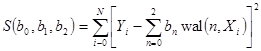Выборки мгновенных значений сигнала проводили через одинаковые интервалы времени, которые составляли 1/16 периода сигнала. Значения коэффициентов b0, b1 и b2, при которых целевая функция принимала минимальное значение, определяли из решения следующей системы уравнений:
.
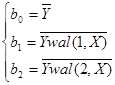По найденным коэффициентам b0, b1 и b2 вычисляли параметры регистрируемого сигнала:
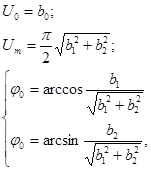
где 
- постоянная составляющая сигнала, Um – амплитуда сигнала, φ0 – начальная фаза.
Для иллюстрации возможности данного метода по определению параметров синусоидальных сигналов при наличии случайной помехи был проведен численный эксперимент, в ходе которого обрабатывались массивы данных , содержащий N=512 отсчетов. Они были получены по следующим формулам:
где номер отсчета i последовательно принимал значения i = 0, 1, …, 511; амплитуда сигнала принималась равной Um=1 В; начальная фаза сигнала устанавливалась φ0 = 33,3˚; число точек, приходящихся на один период сигнала равнялось K = 16; Pi – случайная величина, значение которой находилось в интервале [-0,1; 0,1]. Было сгенерировано 10 массивов данных. Для них рассчитывались амплитуда и начальная фаза сигнала путем аппроксимации соответствующих массивов данных функциями Уолша. Результаты расчетов приведены в таблице 1. В этой же таблице приведены аналогичные результаты, полученные путем аппроксимации исходных сигналов тригонометрическими функциями. В ней же представлены средние значения <Um> и <φ0> и стандартные отклонения для каждого рассмотренного случая. Полученные результаты показывают, что начальные фазы сигнала и его амплитуда, определенные разными методами, с точностью до стандартных отклонений совпадают с истинными значениями.
Таблица 1
Результаты расчетов амплитуды и начальной фазы гармонического сигнала при наличии случайной помехи
|
№ опыта |
Параметры сигнала |
|||
|
Аппроксимация функциями Уолша |
Аппроксимация тригонометрическими функциями |
|||
|
Um, В |
φ0, градусы |
Um, В |
φ0, градусы |
|
|
1 |
1,0008 |
32,903 |
0,9935 |
32,841 |
|
2 |
1,0094 |
33,242 |
1,0015 |
33,364 |
|
3 |
1,0076 |
33,754 |
1,0016 |
33,541 |
|
4 |
1,0114 |
33,312 |
1,0046 |
33,417 |
|
5 |
1,0305 |
32,794 |
1,0167 |
32,925 |
|
6 |
0,9941 |
33,559 |
0,9891 |
33,536 |
|
7 |
1,0160 |
33,217 |
1,0032 |
33,363 |
|
8 |
1,0147 |
33,077 |
1,0016 |
33,281 |
|
9 |
0,9972 |
33,333 |
0,9939 |
33,122 |
|
10 |
1,0113 |
33,716 |
1,0025 |
33,492 |
|
Среднее арифметическое |
1,0093 |
33,291 |
1,0008 |
33,288 |
|
Стандартное отклонение |
0,0105 |
0,3198 |
0,0076 |
0,2482 |
Поскольку функции Уолша принимали значения либо +1, либо -1, то операция умножения сводилась к смене знака соответствующих величин при их суммировании. Так как в процессе измерений данные поступали от аналого-цифрового преобразователя, то они имели целочисленный формат, и операции с плавающей точкой выполнялись только на заключительном этапе. Таким образом, существенно снизились требования, предъявляемые к производительности микроконтроллера, который проводил данную обработку.
При вихретоковом контроле использовали параметрический преобразователь накладного типа, который хорошо зарекомендовал себя при решении различных задач [7-9]. Он имел одну катушку индуктивности и преобразовывал параметры объекта контроля в комплексное сопротивление. Индуктивность и активное сопротивление датчика на различных частотах находили как:
,
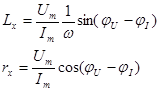где Um – амплитуда напряжения, Im – амплитуда силы тока, φU – начальная фаза напряжения, φI – начальная фаза силы тока, ω – циклическая частота переменного тока.
Результаты измерений
Для проверки работоспособности данного устройства были проведены измерения на алюминиевом сплаве АМг5 с использованием накладного датчика на четырех фиксированных частотах: 300 Гц, 500 Гц, 1 кГц и 3 кГц. Толщина диэлектрического зазора между датчиком и проводящей поверхностью образца изменялась от 0 до 240 мкм. Результаты измерений приведены на рис. 4 в виде экспериментальных точек (L0 – индуктивность датчика без контролируемого образца на фиксированной частоте ω; ΔL=Lx-L0 – изменение индуктивности датчика на фиксированной частоте ω при наличии в зоне контроля проводящего объекта; ΔR=rx-r0, rx и r0 – активные сопротивления датчика при наличии образа и без него соответственно). Для наглядности экспериментальные точки, соответствующие одному образцу, соединены пунктирной линией. Значения толщин диэлектрических покрытий приведены на этом же рисунке. Видно, что кривые, описывающие годографы при разных зазорах, заметно сдвигаются друг относительно друга, причем расхождение между ними больше в нижней части кривых, относящейся к интервалу более высоких частот. Это связано с тем, что увеличение величины диэлектрического зазора приводит к уменьшению влияния параметров проводящего объекта на импеданс датчика, и согласуется с литературными данными [6].
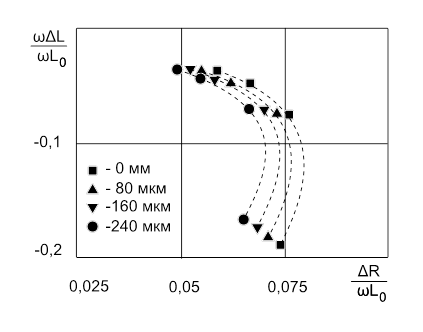
Рис. 4. Влияние толщины диэлектрических покрытий на характеристики накладного параметрического датчика.
Заключение
Применение микропроцессорного вихретокового устройства для анализа результатов вихретоковых измерений позволяет уменьшить влияние случайных факторов, искажающих результат измерений. Полученные результаты хорошо согласуются с теоретическими расчетами, приведенными в литературе, что позволяет сделать заключение о возможности применения данного устройства для контроля толщины диэлектрических покрытий на алюминиевых сплавах.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0063) в рамках реализации Постановления Правительства РФ № 218.
Рецензенты:
Тарасов С.Ю., д.т.н., ведущий научный сотрудник ИФПМ СО РАН, Институт физики прочности и материаловедения СО РАН, г. Томск.
Колубаев А.В., д.ф.-м.н., профессор, заведующий лабораторией физики упрочнения поверхности ИФПМ СО РАН, Институт физики прочности и материаловедения СО РАН, г. Томск.
Библиографическая ссылка
Герусов А.В., Лаптев А.Ю., Егоров А.В., Герусов А.В., Герусов А.В., Лаптев А.Ю. ВИХРЕТОКОВАЯ ДИАГНОСТИКА АЛЮМИНИЕВЫХ СПЛАВОВ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15705 (дата обращения: 20.04.2024).