Сушка является важнейшей частью процесса изготовления различных изделий из древесины [4, 2]. Чем меньше влажность древесины, тем меньше она подвержена растрескиванию и рассыханию. Сушка может производиться несколькими способами. Атмосферная сушка или сушка на открытом воздухе под навесом отличается простотой и доступностью. Тем не менее этот процесс протекает очень медленно – от нескольких месяцев до нескольких лет. Применяется также сушка древесины в стружке, камерная сушка перегретым паром и топочным газом, сушка с использованием токов высокой частоты. Одним из путей повышения скорости сушки оцилиндрованнных бревен без образования трещин является выполнение технологических отверстий [1, 3]. В то же время использование таких отверстий связано со снижением несущей способности бревен. Поэтому существенное значение имеет разработка методики расчета бревна, которая позволит подобрать расположение и диаметр отверстия с обеспечением требуемой прочности бревна в процессе его эксплуатации.
Цель исследования – разработка методики численного моделирования напряженно-деформированного состояния деревянных бревен с продольным отверстием для сушки и подбора геометрических параметров отверстия.
Методы исследования – численные методы механики деформируемого твердого тела.
Расчетная схема и система конечных элементов для анализа деформаций бревен Методика исследования отрабатывалась на примере расчета оцилиндрованных сосновых бревен диаметром D=220 мм, используемых в конструкции наружных стен типового деревянного дома. В соответствии с принципом Сен-Венана подробно изучалось напряженное состояние одного из бревен (обозначено цифрой 1) во взаимодействии с двумя соседними бревнами – 2 и 3 (рисунок 1). Расчет выполнялся для одного погонного метра стены. При этом полагалось, что определяющим для работы рассматриваемого объекта является статический эквивалент Q вертикальных сил q, действующих на верхнее бревно 2. Эти силы равномерно распределялась по горизонтали. Значение Q определяется положением бревна 1 по высоте стены, особенностями конструкции и эксплуатации дома.
В расчетной схеме полагалось, что бревна находятся в условиях плоского деформированного состояния [10]. В каждом из бревен выполнено технологическое отверстие для сушки изнутри. Материал бревен представлялся как ортотропный. Контактное взаимодействие между бревнами учитывалось с помощью односторонних связей 4, перпендикулярных соприкасающимся поверхностям. При этом силы трения не рассматривались. Задавались внешние вертикальные связи 5 в виде шарнирно-стержневых опор. Кроме того, вводились статически определимые связи, обеспечивающие геометрическую неизменяемость системы.
Плоское деформированное состояние описывалось с помощью разрабатываемых уточненных треугольных конечных элементов. Связи 4 представлялись на основе ферменных конечных элементов. При этом в процессе расчета контролировалось, чтобы деформации в этих конечных элементах были отрицательными. Предусматривалось при возникновении растяжения хотя бы в одном из ферменных элементов выполнение итерационного процесса, предусматривающего удаление контактных стержней, работающих на растяжение, и включение в конечно-элементную модель стержней, для которых получались деформации сжатия. Следует, тем не менее, отметить, что для рассмотренных расчетных случаев деформации растяжения в этих связях не фиксировались.
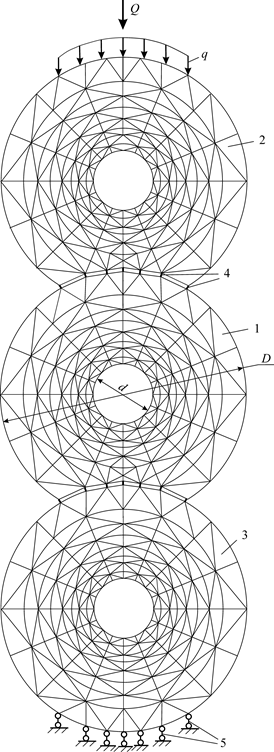
Рис.1. Схема конечно-элементной модели трех бревен при центральном расположении отверстий
В ходе расчетов рассматривалось влияние диаметра и смещения отверстия от центра бревна 1 на его напряженно-деформированное состояние. Принималось во внимание три диаметра d отверстия: 50, 66 и 80 мм. Для диаметра d = 50 мм анализировалось также расположение центра отверстия на 15 и 25 мм выше центра бревна.
Построение уточненных конечных элементов для исследования напряженно-деформированного состояния оцилиндрованных бревен Предложенная в работах [5, 6, 9] предельная схема метода конечных элементов позволяет существенно расширить возможность построения эффективных конечно-элементных моделей повышенной точности. Особенностью этого подхода является отказ от описания перемещений по всей площади конечного элемента. Аппроксимация перемещений осуществляется по отдельным отрезкам на границе и внутри области элемента, что существенно расширяет возможности создания простых, но достаточно эффективных конечно-элементных дискретизаций.
Рассмотрим треугольный конечный элемент, описывающий плоское деформированное состояние (рисунок 2). В соответствии со схемой Аллмана [8] введем, кроме угловых узлов I, II, III, вспомогательные узлы 1, 2, 3, расположенные на серединах сторон треугольника. В узлах I, II, III определим по два перемещения (Ui и Vi) в направлениях осей декартовой системы координат Оxy.
Свяжем с каждым из узлов 1, 2, 3 по одному дополнительному перемещению di, перпендикулярному стороне треугольника, на которой расположен узел. Полные перемещения точек 1, 2, 3 будут представляться в виде сумм перемещений, выражаемых через величины Ui, Vi, и перемещений di.
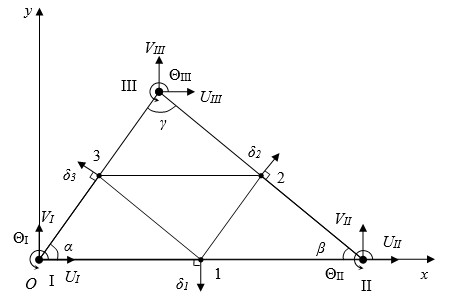
Рис. 2. Треугольный конечный элемент
Первоначально рассмотрим составляющие деформаций для этих точек, обусловленные только перемещениями Ui, Vi. В соответствии с предельной схемой метода конечных элементов линейные деформации от этих перемещения для точки 1 в направлениях ![]() ,
,![]() ,
, ![]() определим следующим образом:
определим следующим образом:
![]() ;
; ![]() ;
; ![]() , (1)
, (1)
где ui, vi (i=1, 2, 3) ‑ перемещения точек 1, 2, 3 в направлениях осей Оx и Оy, вычисляемые с помощью выражений
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; (2)
; (2)
a, b – углы, показанные на рисунке 2; lI, II, l12, l13 ‑ длины отрезков I-II, 1-2 и 1-3.
Подставив зависимости (2) в равенства (1), получим
![]() ;
; ![]() . (3)
. (3)
Аналогично придем к формулам для нахождения деформаций в точке 2 в направлениях ![]() ,
,![]() ,
, ![]() и в точке 3 в направлениях
и в точке 3 в направлениях ![]() ,
, ![]() ,
,![]() .
.
Считаем, что дополнительные перемещения точек отрезков 1-2 и 1-3, связанные с перемещениями d1, d2, d3, изменяются вдоль этих отрезков по линейным законам. Тогда для точки 1 дополнительные линейные деформации в направлениях ![]() ,
, ![]() будут определяться зависимостями
будут определяться зависимостями
![]() ;
; ![]() . (4)
. (4)
Учитывая выражения Аллмана [9] в равенствах (4), запишем
![]() ; (5)
; (5)
![]() , (6)
, (6)
где ![]() ,
, ![]() ,
,![]() – углы поворота в угловых точках треугольника.
– углы поворота в угловых точках треугольника.
Аналогичные выражения могут быть получены для точек 2 и 3. Матрица деформаций ![]() для точки i (i = 1, 2, 3) определяется равенством
для точки i (i = 1, 2, 3) определяется равенством
![]() , (7)
, (7)
где ![]() – вектор полных линейных деформаций для отрезков, связанных с этой точкой:
– вектор полных линейных деформаций для отрезков, связанных с этой точкой:
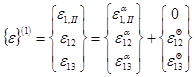 . (8)
. (8)
Будем рассматривать точки 1, 2, 3 как точки интегрирования [5]. Тогда получим следующее выражение для вычисления матрицы жесткости конечного элемента:
![]() , (9)
, (9)
где V – объем элемента; ![]() – матрица упругости плоского деформированного состояния для ортотропного материала.
– матрица упругости плоского деформированного состояния для ортотропного материала. ![]() – матрица преобразования деформаций для i-й точки при переходе от вектора
– матрица преобразования деформаций для i-й точки при переходе от вектора ![]() к вектору
к вектору![]() .
.
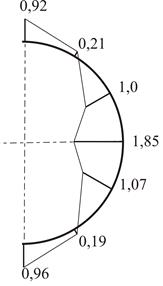
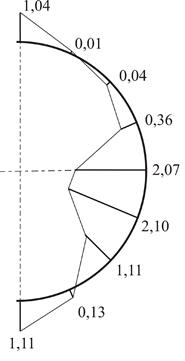
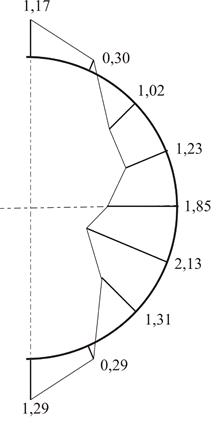
Результаты исследования деформаций бревен Особенности напряженного состояния анализировались при базовой суммарной силе ![]() кН/м. Для всех рассматриваемых вариантов бревна наибольшие по абсолютныой величине нормальные напряжения получились на контуре отверстия. Эпюры этих напряжений для принимаемых во внимание диаметров центрированного отверстия представлены на рисунке 3. Увеличение диаметра отверстия с 50 мм до 66 мм привело к повышению максимальных значений smax растягивающих напряжений и максимальных абсолютных значений
кН/м. Для всех рассматриваемых вариантов бревна наибольшие по абсолютныой величине нормальные напряжения получились на контуре отверстия. Эпюры этих напряжений для принимаемых во внимание диаметров центрированного отверстия представлены на рисунке 3. Увеличение диаметра отверстия с 50 мм до 66 мм привело к повышению максимальных значений smax растягивающих напряжений и максимальных абсолютных значений ![]() сжимающих напряжений соответственно на 16 и 14 %, с 50 до 80 мм – на 34 и 15 %. Смещение отверстия диаметром 50 мм на 15 мм вверх дало увеличение
сжимающих напряжений соответственно на 16 и 14 %, с 50 до 80 мм – на 34 и 15 %. Смещение отверстия диаметром 50 мм на 15 мм вверх дало увеличение ![]() при растяжении на 34 % и
при растяжении на 34 % и ![]() при сжатии на 9 %. При смещении на 25 мм вверх получилось уменьшение smax при растяжении на 14 % и увеличение
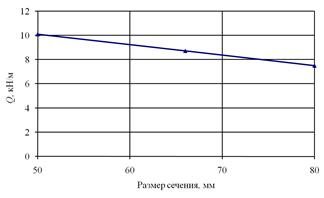
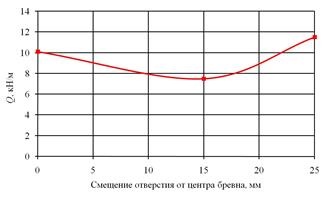
при сжатии на 9 %. При смещении на 25 мм вверх получилось уменьшение smax при растяжении на 14 % и увеличение ![]() при сжатии на 2 %. На рисунках 4, 5 приведены графики максимально допустимых значений вертикальной погонной нагрузки на бревно, полученные с учетом расчетных сопротивлений для сосны при деформациях поперек волокон [7]. Эти графики могут быть использованы для выбора геометрических параметров отверстия в зависимости от нагруженности бревна.
при сжатии на 2 %. На рисунках 4, 5 приведены графики максимально допустимых значений вертикальной погонной нагрузки на бревно, полученные с учетом расчетных сопротивлений для сосны при деформациях поперек волокон [7]. Эти графики могут быть использованы для выбора геометрических параметров отверстия в зависимости от нагруженности бревна.
|
|
|
 |
|
а |
б |
в |
Рис. 3. Распределение нормальных напряжений, МПа по окружности центрального отверстия диаметром 50 (а), 66 (б) и 80 (в) мм
|
|
|
|
Рис. 4. Зависимость допустимой силы от диаметра отверстия |
Рис. 5. Зависимость допустимой силы от смещения отверстия |
Выводы
1. Разработана методика определения геометрических параметров продольного отверстия для сушки бревен при условии обеспечения прочности бревна для заданной его нагруженности в конструкции наружных стен типового деревянного дома.
2. Выполнено исследование напряженно-деформированного состояния сосновых бревен в наружных стенах деревянных срубов с центральными продольными отверстиями диаметрами 50, 66, 80 мм и отверстиями диаметром 50 мм со смещением от центра бревна вверх на расстояние 15 и 25 мм.
3. Проведенные расчеты бревен с отверстиями для сушки показали, что наиболее опасными при рассматриваемых нагружениях являются напряжения по контуру отверстий.
4. Полученные результаты могут быть использованы при назначении диаметра и положения отверстия в зависимости от действующей нагрузки на бревно. При этом в одной и той же стене бревенчатого здания исполнение отверстия может быть разным в зависимости от положения бревна по высоте конструкции.
Рецензенты:
Ерохин В.В., д.т.н., профессор, профессор кафедры автоматизированных информационных систем и технологий, ФГБОУ ВПО «Брянская государственный университет имени академика И.Г. Петровского» Министерства образования и науки Российской Федерации, г. Брянск;
Плотников В.В., д.т.н., профессор, проректор по научной и инновационной деятельности, заведующий кафедрой «Строительное производство», ФГБОУ ВПО «Брянская государственная инженерно-технологическая академия» Министерства образования и науки Российской Федерации, г. Брянск.
Библиографическая ссылка
Серпик И.Н., Мироненко И.В., Лукаш А.А., Удалов С.Е. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ОТВЕРСТИЯ ДЛЯ СУШКИ ОЦИЛИНДРОВАННЫХ БРЕВЕН // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15693 (дата обращения: 23.02.2026).