Задача составления оптимальной смеси является одной из наиболее распространённых технологических задач оптимизации. Она применяется в различных областях: нефтепереработке, производстве минеральных удобрений и кормов для животных, составлении оптимальных рационов и диет.
Цели настоящей работы – исследовать подклассы традиционной задачи поиска оптимальной смеси; поставить задачу оптимальной композиции материалов в виде, достаточно лёгком для составления компьютерной программы, путём модернизации классической задачи поиска смеси; используя найденные способы модернизации сформулировать задачу оптимизации компонентного состава на конкретном примере; выявить основные особенности полученных в ходе исследования задач.
Классическая задача поиска оптимальной смеси
В общем виде классическая задача о поиске оптимальной смеси выглядит следующим образом: по заданному ассортименту компонентов при известных их определённых характеристиках и стоимости составить смесь (композицию компонентов), удовлетворяющую необходимым условиям с минимальными денежными затратами [4].
Пусть существует n различных исходных компонентов и m питательных веществ, химических элементов и т.п. Обозначим через ![]() массу j-го вещества, содержащуюся в единице массы i-го компонента; через
массу j-го вещества, содержащуюся в единице массы i-го компонента; через ![]() обозначим минимально необходимую массу j-го вещества в готовой смеси. Через
обозначим минимально необходимую массу j-го вещества в готовой смеси. Через ![]() обозначим искомую массу i-го компонента, входящего в смесь. При этом
обозначим искомую массу i-го компонента, входящего в смесь. При этом ![]() .
.
Через величину ![]() выражается общее содержание j-го вещества в смеси, которое не должно быть меньше минимально необходимого
выражается общее содержание j-го вещества в смеси, которое не должно быть меньше минимально необходимого ![]() :
:
![]() .
.
Если ![]() – стоимость i-го исходного компонента, то стоимость всей смеси определяется линейной формой
– стоимость i-го исходного компонента, то стоимость всей смеси определяется линейной формой ![]() .
.
Таким образом, математическая формулировка классической задачи поиска оптимальной смеси в общем виде может быть записана следующим образом:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Сформулированная задача (1) – (3) представляет собой одну из типичных задач линейного программирования, для решения которых используются известные математические методы, такие как симплекс-метод, двойственный, модифицированный симплекс-метод и многие другие, подробно описанные в литературе как зарубежных [5,9] так и отечественных [3,4,6,10] авторов. Этот факт позволяет в рамках задачи о поиске оптимальной смеси рассматривать и такие типы задач, как, например, «задача о диете», «задача о ранце», поиск оптимальной композиции материалов и т.д., так как они по своей сути принадлежат одному классу задач. Многочисленные и самые разнообразные задачи поиска оптимальных смесей могут быть сформулированы подобным образом. При этом слово «смесь» можно понимать в различных смыслах: рацион, сплав и так далее [4]. Однако существуют ситуации, когда задача составления оптимальных смесей в классической линейной постановке оказывается неприменимой.
Оптимальная композиция материалов
Задачи составления оптимальных композиций из материалов, которые должны обладать определёнными свойствами и минимальной себестоимостью образуют подкласс задач о смесях и нуждаются в расширении и уточнении классической задачи, рассмотренной выше. Число исходных материалов может быть достаточно большим [7], и поэтому решить такую задачу перебором вариантов представляется возможным лишь в приближённом виде. Причём неизвестно, насколько близким к оптимальному получится решение. Как правило, на производстве такие задачи решаются квалифицированными специалистами.
Для формализации решения задач этого класса можно предложить модель математического программирования в целочисленной постановке.
Пусть имеется ![]() групп исходных материалов, в каждую из которых входит
групп исходных материалов, в каждую из которых входит ![]() видов однотипных материалов, отличающихся своими характеристиками.
видов однотипных материалов, отличающихся своими характеристиками.
Из этих материалов необходимо получить изделие, обладающее свойствами, которые зависят от характеристик исходных материалов. Эти зависимости определяются специалистами-технологами на производстве экспериментальным путём. Из каждой группы материалов нужно выбрать всего один.
Пусть заданы ![]() свойств, которыми должно обладать вырабатываемое изделие, их значения не должны быть ниже некоторой определённой границы качества
свойств, которыми должно обладать вырабатываемое изделие, их значения не должны быть ниже некоторой определённой границы качества ![]() . Каждый из исходных материалов имеет значение соответствующих свойств
. Каждый из исходных материалов имеет значение соответствующих свойств ![]() . Считаем зависимость свойств вырабатываемого изделия от свойств исходных материалов линейной. Обозначим
. Считаем зависимость свойств вырабатываемого изделия от свойств исходных материалов линейной. Обозначим ![]() – коэффициенты, характеризующие влияние свойств исходных материалов на свойства вырабатываемого изделия;
– коэффициенты, характеризующие влияние свойств исходных материалов на свойства вырабатываемого изделия; ![]() – цена r-го материала из i-й группы;
– цена r-го материала из i-й группы; ![]() – r-й материал из i-й группы.
– r-й материал из i-й группы.
Чтобы сформулировать задачу, введём булевы переменные:
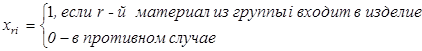 (4)
(4)
В каждой из групп в соответствии с условиями задачи необходимо выбрать только один материал. Это условие запишем в виде ограничения следующим образом:
![]() (
(![]() ) (5)
) (5)
Ограничения по свойствам изделия принимают следующий вид:
![]() (
(![]() ) (6)
) (6)
Минимум затрат на производство изделия запишем в качестве целевой функции:
![]() (
(![]() ) (7)
) (7)
В качестве целевой функции могут быть выбраны и другие показатели, например минимальный вес изделия и др. Рассмотренная постановка достаточно проста и задача (4) – (7) может быть решена известными методами целочисленного программирования.
Однако при практической реализации задачи могут возникнуть трудности, связанные с большой размерностью задачи. В зависимости от отрасли применения количество разновидностей материалов в однородных группах может достигать нескольких сотен, а иногда тысяч [7], что обуславливает большую трудоёмкость формирования задачи. Решить эту проблему можно с помощью специального программного обеспечения, используя модули параллельных вычислений в сервис-ориентированной архитектуре [8].
Также, ещё одна из трудностей применения задачи заключается в том, что зависимости свойств изделия от свойств исходных материалов определяются экспериментальным путём, а это, в свою очередь, влёчёт за собой большие затраты труда. Кроме того, задача является многокритериальной и при решении её с разными критериями могут получиться различные результаты. Какой из них следует выбрать в каждом конкретном случае должно решать лицо, принимающее решения (ЛПР).
Постановка задачи оптимальной композиции материалов для гофрированного картона
Для более глубокого понимания возможностей применения задачи, поставленной выше, а так же в качестве достаточно показательного примера рассмотрим задачу составления оптимальной композиции материалов при производстве гофрированного картона (ГК).
Пусть требуется подобрать компоненты для трёхслойного ГК. Минимизировать стоимость компонентов, вес и толщину готового ГК. На первый взгляд задача может показаться несложной, однако, для эффективного её решения требуется грамотно построенная задача математического программирования, учитывающая, по возможности, все основные зависимости между исходными материалами и готовым продуктом.
Основными исходными компонентами, влияющими на качество выпускаемой продукции при производстве ГК, являются: картон для плоских слоёв (КПС) и бумага для гофрирования (БГ). Клей также входит в число исходных компонентов, однако зависимости основных характеристик ГК, выражаемых в числовом эквиваленте, таких как «абсолютное сопротивление продавливанию» и «сопротивление торцевому сжатию» [1] от характеристик клея не определены. В связи с этим обстоятельством, клей не будет рассмотрен в задаче оптимальной композиции материалов для ГК. При проведении практических расчётов и построении программного обеспечения, решающего задачу оптимизации компонентов ГК, можно рекомендовать делать выбор клея исходя из его стоимости, расхода, возможностей производственной линии и требуемых характеристик выпускаемой продукции, не выражаемых в числовом эквиваленте. Это такие характеристики, как: возможность применения для упаковывания пищевой продукции, воздухопроницаемость, влагостойкость и пр.
Итак, имеется ![]() видов КПС и
видов КПС и ![]() видов БГ. Имеются характеристики исходных КПС и БГ, а так же характеристики ГК требуемой марки
видов БГ. Имеются характеристики исходных КПС и БГ, а так же характеристики ГК требуемой марки ![]() (
(![]() – вид характеристики) и зависимости результирующих характеристик от свойств исходных компонентов, полученные экспериментальным путём и достаточно хорошо описанные в специализированной литературе [2]. Имеются себестоимости картонов
– вид характеристики) и зависимости результирующих характеристик от свойств исходных компонентов, полученные экспериментальным путём и достаточно хорошо описанные в специализированной литературе [2]. Имеются себестоимости картонов ![]() и бумаги
и бумаги ![]() .
.
Неизвестные представим в виде булевых переменных.
Для верхнего слоя КПС:
![]() (
(![]() ). (8)
). (8)
Для нижнего слоя КПС:
![]() (
(![]() ). (9)
). (9)
Для БГ:
![]() (
(![]() ). (10)
). (10)
Введём ограничения по переменным:
![]() ; (11)
; (11)
![]() ; (12)
; (12)
![]() . (13)
. (13)
Ограничения (11) – (13) говорят о том, что из исходного множества должен быть выбран только один вид каждого материала.
Дополним задачу ограничениями по характеристикам:
![]() (
(![]() ), (14)
), (14)
где ![]() – коэффициент влияния свойств вида s i-го КПС на свойства ГК;
– коэффициент влияния свойств вида s i-го КПС на свойства ГК; ![]() – коэффициент влияния свойств вида s j-й БГ на свойства ГК;
– коэффициент влияния свойств вида s j-й БГ на свойства ГК; ![]() – характеристики ГК требуемой марки; s – вид характеристики.
– характеристики ГК требуемой марки; s – вид характеристики.
Марка ГК определяется исходя из наихудших значений его характеристик по таблице ГОСТ Р 52901-2007 [1], поэтому значения прогнозируемых характеристик продукта должны быть равны известным значениям для требуемой марки ГК, или превосходить их, что отражает ограничение (14).
Целевые функции принимают следующий вид:
![]() ; (15)
; (15)
![]() ; (16)
; (16)
![]() . (17)
. (17)
Здесь ![]() – стоимость транспортировки единицы i-го КПС;
– стоимость транспортировки единицы i-го КПС; ![]() – стоимость транспортировки единицы j-й БГ;
– стоимость транспортировки единицы j-й БГ; ![]() – масса единицы i-го КПС;
– масса единицы i-го КПС; ![]() – масса единицы j-й БГ;
– масса единицы j-й БГ; ![]() – толщина i-го КПС. БГ не включается в целевую функцию (17) так как её толщина практически не влияет на толщину готового изделия – бумага гофрируется в соответствии с поставленной на производстве задачей.
– толщина i-го КПС. БГ не включается в целевую функцию (17) так как её толщина практически не влияет на толщину готового изделия – бумага гофрируется в соответствии с поставленной на производстве задачей.
Таким образом нами получена задача (8) – (17) для составления оптимальной композиции материалов для производства ГК, учитывающая основные зависимости между исходными материалами и готовым продуктом, а так же включающая в себя важнейшие критерии, которыми может руководствоваться технолог на предприятии.
Выводы
Анализируя полученные результаты, можно утверждать, что задачи (4) – (7) и (8) – (17), исходя из ограничений (4) и (8) – (10) соответственно, входят в подкласс линейных задач целочисленного программирования с булевыми переменными [3]. При этом, задача поиска оптимальной композиции компонентов ГК в постановке (8) – (17) фактически представляет собой задачу о смеси, несмотря на то, что на практике отсутствует физический процесс перемешивания. Вместо этого компоненты соединяются, образуя готовое изделие, однако это не меняет сути самой задачи, ведь итогом её решения и в одном и в другом случае является рекомендованный набор компонентов для объединения. Таким образом, для поиска оптимальной композиции компонентов ГК можно применять стандартные математические методы решения. Так как задача (8) – (17) является многокритериальной, то расчёт необходимо произвести по каждому критерию и оставить возможность окончательного выбора для ЛПР. Также для решения этой проблемы можно использовать векторную оптимизацию или другие методы сведения задачи к однокритериальной.
Заключение
В заключении нужно отметить, что поставленная в данной работе задача (4) – (7) является универсальной для класса задач поиска оптимальной композиции материалов и может эффективно применяться производстве для множества типов продукции, начиная от ГК и заканчивая сложными многоэлементными печатными платами. Везде, где технологический процесс предполагает соединение компонентов разных типов для получения конечного изделия, разработанная задача (4) – (7) позволит формализовать процесс решения задачи поиска оптимальной композиции, открывая возможность использования известных и проверенных математических методов. При этом задача математического программирования может быть взята за основу модулей расчёта в специализированном программном обеспечении, что позволит автоматизировать процесс решения задачи [7]. Внедрение полученных результатов может способствовать увеличению точности прогнозируемого уровня качества продукции, сокращению затрат на производство и снижению трудоемкости расчетов.
Рецензенты:
Каширин И.Ю., д.т.н., профессор, ФГБОУ ВПО "РГРТУ", г. Рязань;
Пылькин А.Н., д.т.н., профессор, ФГБОУ ВПО "РГРТУ", г. Рязань.
Библиографическая ссылка
Селиванов Е.В. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОЙ КОМПОЗИЦИИ МАТЕРИАЛОВ КАК РАЗНОВИДНОСТИ ЗАДАЧИ О СМЕСЯХ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15599 (дата обращения: 19.02.2026).



