Эффективность управленческих решений по инвестированию конкурсных проектов (КП) в различных отраслях экономики во многом зависит от того, насколько адекватно и обоснованно выполнены классификация, упорядочение и последующий отбор КП, заключающиеся в выборе таких КП из числа возможных, в которых будет оптимизирована общая ценность, в максимальной степени обеспечивающая достижение поставленных целей. Наличие большого количества характеристик оценивания, противоречивость требований, неуверенность экспертов при выставлении оценок КП, ошибки в выборе приоритетов усложняют процедуру принятия решений по классификации, упорядочению и отбору КП.
Эксперты, осуществляющие классификацию, упорядочение и отбор КП, должны выявить достоинства и недостатки КП, а также оценить последствия принятия их к реализации, основываясь на своих субъективных представлениях и знаниях в конкретной предметной области. Однако довольно часто даже высококвалифицированные специалисты могут давать противоречивые оценки КП по характеристикам оценивания, а также и оценки значимости самих характеристик. Кроме того, иногда эксперты способны определить лишь интервалы принадлежности оценок, затрудняясь выставить однозначные чёткие оценки по какой-либо балльной шкале.
Несмотря на наличие разнообразных подходов к решению задачи классификации, упорядочения и отбора различных объектов на основе групповых экспертных оценок [1 – 5, 8, 9], существует необходимость в разработке математического аппарата, позволяющего принимать адекватные и обоснованные классификационные решения с использованием субъективных качественных данных, представленных, в том числе, в виде интервальных оценок [6, 10] и соответствующих систем поддержки принятия решений [7].
Задача классификации КП может быть сформулирована как задача разбиения совокупности КП на два класса: «Принять КП к реализации» и «Отклонить КП» по результатам группового экспертного оценивания КП по некоторой совокупности характеристик, а задача упорядочения КП – как задача сортировки КП в соответствии с некоторым алгоритмом. Один из перспективных подходов к решению задачи классификации и упорядочения, позволяющий учесть все, в том числе и противоречивые, групповые экспертные оценки, основан на применении инструментария теории мультимножеств. Данный подход предполагает использование классической балльной шкалы оценивания, на основе которой эксперты выставляют однозначные чёткие оценки КП по характеристикам оценивания, применяемые в дальнейшем как для формирования обобщающих решающих правил классификации (ОРПК) КП, так и для упорядочения КП. В случае, когда эксперты готовы определить лишь интервалы принадлежности оценок (интервальные оценки) КП по характеристикам оценивания, актуальной становится задача разработки подхода к комплексному анализу КП с применением лингвистической шкалы оценивания, позволяющей формировать различные классификационные стратегии – консервативную, нейтральную и рискованную – на основе интервальных оценок КП по характеристикам оценивания, и инструментария теории мультимножеств [8], обеспечивающего учет всех, в том числе и противоречивых, групповых экспертных оценок КП по характеристикам оценивания.
Теоретическая часть. Пусть ![]() – совокупность КП;
– совокупность КП; ![]() – совокупность характеристик, по которым оцениваются КП, а количество экспертов равно
– совокупность характеристик, по которым оцениваются КП, а количество экспертов равно ![]() . Классический подход к задаче разработки ОРПК КП предполагает, что экспертное оценивание КП по характеристикам оценивания производится по чёткой балльной шкале. Зачастую эксперт может оказаться в ситуации, когда он затрудняется дать чёткие числовые оценки КП по характеристикам оценивания, но при этом может указать некоторые интервалы, которым принадлежат эти оценки.
. Классический подход к задаче разработки ОРПК КП предполагает, что экспертное оценивание КП по характеристикам оценивания производится по чёткой балльной шкале. Зачастую эксперт может оказаться в ситуации, когда он затрудняется дать чёткие числовые оценки КП по характеристикам оценивания, но при этом может указать некоторые интервалы, которым принадлежат эти оценки.
Для повышения качества классификационных решений на основе неточных знаний экспертов как об оценках КП по характеристикам оценивания, так и о значимости самих характеристик предлагается отказаться от применения традиционной четкой балльной шкалы оценивания и использовать лингвистическую шкалу, позволяющую реализовать принципы описания и обработки неточных данных на основе лингвистических переменных [6, 10]. В случае применения лингвистического подхода каждому КП по каждой характеристике оценивания будет выставляться не чёткая числовая оценка, а некоторая интервальная оценка вида ![]() [6, 10]. Левая и правая границы интервала
[6, 10]. Левая и правая границы интервала ![]() могут быть сопоставлены, соответственно, чисто консервативной и чисто рискованной стратегиям оценивания (стратегиям принятия решений), а середина этого интервала – нейтральной стратегии. Так как для расчетов будут использоваться те или иные различные чёткие числовые оценки КП по характеристикам оценивания, принадлежащие интервалам вида
могут быть сопоставлены, соответственно, чисто консервативной и чисто рискованной стратегиям оценивания (стратегиям принятия решений), а середина этого интервала – нейтральной стратегии. Так как для расчетов будут использоваться те или иные различные чёткие числовые оценки КП по характеристикам оценивания, принадлежащие интервалам вида ![]() , то можно говорить о наличии одной нейтральной стратегии оценивания и некоторого набора консервативных и рискованных стратегий оценивания и, соответственно, принятия решений (в зависимости от того, к каким границам интервальных оценок вида
, то можно говорить о наличии одной нейтральной стратегии оценивания и некоторого набора консервативных и рискованных стратегий оценивания и, соответственно, принятия решений (в зависимости от того, к каким границам интервальных оценок вида ![]() ближе расположены применяемые для расчетов чёткие числовые оценки КП по характеристикам оценивания).
ближе расположены применяемые для расчетов чёткие числовые оценки КП по характеристикам оценивания).
Пусть ![]() – дискретная лингвистическая шкала, где
– дискретная лингвистическая шкала, где ![]() – лингвистическая переменная;
– лингвистическая переменная; ![]() – натуральное число (
– натуральное число (![]() ). Так, при
). Так, при ![]() лингвистическая шкала
лингвистическая шкала ![]() может быть определена как
может быть определена как ![]() = =(«чрезвычайно низкая», «очень низкая», «низкая», «средняя», «высокая», «очень высокая», «чрезвычайно высокая»), где каждый лингвистический терм (например, «низкая») соответствует классической чёткой оценке (–1), которая в случае представления неточных знаний экспертов является одной из границ (левой или правой) интервала оценивания (если знания являются точными, то левая граница будет совпадать с правой) [6, 10]. Во избежание потери лингвистической информации о принимаемом решении, дискретная лингвистическая шкала
= =(«чрезвычайно низкая», «очень низкая», «низкая», «средняя», «высокая», «очень высокая», «чрезвычайно высокая»), где каждый лингвистический терм (например, «низкая») соответствует классической чёткой оценке (–1), которая в случае представления неточных знаний экспертов является одной из границ (левой или правой) интервала оценивания (если знания являются точными, то левая граница будет совпадать с правой) [6, 10]. Во избежание потери лингвистической информации о принимаемом решении, дискретная лингвистическая шкала ![]() может быть расширена на непрерывную лингвистическую шкалу
может быть расширена на непрерывную лингвистическую шкалу ![]() , где
, где ![]() – большое положительное число (
– большое положительное число (![]() ). Тогда, если
). Тогда, если ![]() , то
, то ![]() является исходным лингвистическим термом, в противном случае
является исходным лингвистическим термом, в противном случае ![]() является виртуальным лингвистическим термом [6, 10]. При этом исходные лингвистические термы используются для оценки как характеристик КП, так и значимости этих характеристик, а виртуальные – для реализации вычислений с целью выполнения классификации и упорядочения КП. Применение лингвистического подхода к принятию решений на основе инструментария мультимножеств позволяет рассмотреть различные стратегии формирования ОРПК и упорядочения КП.
является виртуальным лингвистическим термом [6, 10]. При этом исходные лингвистические термы используются для оценки как характеристик КП, так и значимости этих характеристик, а виртуальные – для реализации вычислений с целью выполнения классификации и упорядочения КП. Применение лингвистического подхода к принятию решений на основе инструментария мультимножеств позволяет рассмотреть различные стратегии формирования ОРПК и упорядочения КП.
Ниже рассмотрены основные принципы формирования ОРПК КП и упорядочения КП. Так как каждый КП оценивается несколькими экспертами, то имеется несколько различных вариантов оценивания КП, поскольку оценки экспертов могут быть как схожими, так и противоречивыми. Несогласованность индивидуальных экспертных оценок КП по характеристикам оценивания и оценок значимости самих характеристик может быть вызвана неоднозначностью понимания экспертами решаемой задачи, ошибками и неточностями при оценивании КП, специфичностью знаний экспертов. При принятии решения о классификации КП следует учесть все, даже противоречивые оценки экспертов.
Совокупность КП ![]() может быть представлена как совокупность мультимножеств
может быть представлена как совокупность мультимножеств ![]() [8]. Пусть
[8]. Пусть ![]() – количество оценок
– количество оценок ![]() (
(![]() ) по
) по ![]() -й характеристике;
-й характеристике; ![]() – количество экспертов, давших оценку
– количество экспертов, давших оценку ![]() (
(![]() ;
; ![]() ;
; ![]() ). Пусть
). Пусть ![]() – количество экспертов, давших оценку
– количество экспертов, давших оценку ![]() (
(![]() ;
; ![]() ) принадлежности КП
) принадлежности КП ![]() классу
классу ![]() (
(![]() ) на основе предварительных индивидуальных правил сортировки
) на основе предварительных индивидуальных правил сортировки ![]() . Очевидно, что существуют:
. Очевидно, что существуют: ![]() различных экземпляров каждого КП
различных экземпляров каждого КП ![]() , отличающихся значениями оценок по характеристикам;
, отличающихся значениями оценок по характеристикам; ![]() несовпадающих предварительных индивидуальных сортировок совокупности КП
несовпадающих предварительных индивидуальных сортировок совокупности КП ![]() . Пусть оценки по каждой характеристике упорядочены от худшей к лучшей:
. Пусть оценки по каждой характеристике упорядочены от худшей к лучшей: ![]() (
(![]() );
); ![]() , а данные об особенностях классов и характеристик отсутствуют. Если сформировать совокупность характеристик:
, а данные об особенностях классов и характеристик отсутствуют. Если сформировать совокупность характеристик: ![]() , то каждому КП
, то каждому КП ![]() в соответствие может быть поставлено мультимножество вида [1 – 4, 8]:
в соответствие может быть поставлено мультимножество вида [1 – 4, 8]:
![]() (1)
(1)
где символ «∙» используется для обозначения взаимосвязей между ![]() и
и ![]() , а также между
, а также между ![]() и
и ![]() (
(![]() ;
; ![]() ;
; ![]() ;
; ![]() ).
).
Представление КП ![]() в виде (1) может быть реализовано с помощью правил вида:
в виде (1) может быть реализовано с помощью правил вида:
ЕСЛИ <условия>, ТО <решение>. (2)
Терм <условия> соответствует различным комбинациям значений оценок КП ![]() по характеристикам оценивания. В терм <решение> входят совокупности индивидуальных заключений экспертов по предварительной сортировке КП
по характеристикам оценивания. В терм <решение> входят совокупности индивидуальных заключений экспертов по предварительной сортировке КП ![]() и некоторое правило отнесения КП
и некоторое правило отнесения КП ![]() к определенному классу
к определенному классу ![]() (например, правило большинства голосов, в соответствии с которым КП
(например, правило большинства голосов, в соответствии с которым КП ![]() принадлежит к классу
принадлежит к классу ![]() , если
, если ![]() для всех
для всех ![]() (
(![]() ;
; ![]() )). ОРПК КП должны в наибольшей степени соответствовать всем индивидуальным экспертным оценкам КП по характеристикам и обеспечивать разложение совокупности КП
)). ОРПК КП должны в наибольшей степени соответствовать всем индивидуальным экспертным оценкам КП по характеристикам и обеспечивать разложение совокупности КП ![]() на два класса
на два класса ![]() и
и ![]() наилучшим образом (в смысле близости к предварительным индивидуальным сортировкам). Формирование класса
наилучшим образом (в смысле близости к предварительным индивидуальным сортировкам). Формирование класса ![]() (
(![]() ) может быть реализовано посредством сложения соответствующих ему мультимножеств с учетом всех оценок по всем характеристикам всех КП, входящих в класс
) может быть реализовано посредством сложения соответствующих ему мультимножеств с учетом всех оценок по всем характеристикам всех КП, входящих в класс ![]() (
(![]() ). В мультимножестве
). В мультимножестве ![]() класса
класса ![]() (
(![]() ):
): ![]() элементы
элементы ![]() и
и ![]() (
(![]() ;
; ![]() ;
; ![]() ) могут быть вычислены как суммы соответствующих элементов
) могут быть вычислены как суммы соответствующих элементов ![]() и
и ![]() для КП
для КП ![]() , попавших в класс
, попавших в класс ![]() (
(![]() ). Мультимножество
). Мультимножество ![]() класса
класса ![]() может быть записано как
может быть записано как ![]() (
(![]() ;
; ![]() ), где
), где ![]() и
и ![]() – мультимножества, элементами которых являются соответственно суммы оценок по
– мультимножества, элементами которых являются соответственно суммы оценок по ![]() -й характеристике КП
-й характеристике КП ![]() , попавших в класс
, попавших в класс ![]() (
(![]() ), и суммы оценок классовой принадлежности КП
), и суммы оценок классовой принадлежности КП ![]() , попавших в класс
, попавших в класс ![]() (
(![]() ).
).
Для вычисления расстояния между мультимножествами ![]() и
и ![]() может быть использована метрика Хемминга [8], определяемая как:
может быть использована метрика Хемминга [8], определяемая как:
![]() , (3)
, (3)
где ![]() – коэффициент относительной важности
– коэффициент относительной важности ![]() -й характеристики (
-й характеристики (![]() );
); ![]() .
.
При формировании ОРПК в случае, если коэффициенты относительной важности ![]() (
(![]() ) одинаково важны или их важность неизвестна, то значения коэффициентов
) одинаково важны или их важность неизвестна, то значения коэффициентов ![]() (
(![]() ) полагаются равными друг другу. В дальнейшем значения коэффициентов
) полагаются равными друг другу. В дальнейшем значения коэффициентов ![]() (
(![]() ) могут быть уточнены в соответствии с выводами, полученными при формировании ОРПК.
) могут быть уточнены в соответствии с выводами, полученными при формировании ОРПК.
КП ![]() (
(![]() ) в разложении
) в разложении ![]() , сделанном по результатам предварительных индивидуальных сортировок, образуют наилучшую возможную декомпозицию совокупности КП
, сделанном по результатам предварительных индивидуальных сортировок, образуют наилучшую возможную декомпозицию совокупности КП ![]() на 2 класса. Расстояние
на 2 класса. Расстояние ![]() между мультимножествами
между мультимножествами ![]() и
и ![]() является предельно возможным расстоянием в пространстве мультимножеств между КП, входящими в разные классы. При идеальных предварительных индивидуальных сортировках КП расстояние
является предельно возможным расстоянием в пространстве мультимножеств между КП, входящими в разные классы. При идеальных предварительных индивидуальных сортировках КП расстояние ![]() вычисляется как
вычисляется как ![]() [8].
[8].
Поиск ОРПК КП сводится к ![]() оптимизационным задачам по характеристикам
оптимизационным задачам по характеристикам ![]() (
(![]() ):
):
![]() . (4)
. (4)
Для каждой характеристики ![]() (
(![]() ) необходимо найти новые мультимножества
) необходимо найти новые мультимножества ![]() и
и ![]() , располагающиеся на максимально возможном расстоянии в пространстве мультимножеств и принадлежащие разным классам. Мультимножество
, располагающиеся на максимально возможном расстоянии в пространстве мультимножеств и принадлежащие разным классам. Мультимножество ![]() (
(![]() ;
; ![]() ) может быть представлено в виде суммы двух подмультимножеств
) может быть представлено в виде суммы двух подмультимножеств ![]() [8]. Решение каждой из задач (4) выражается через подмультимножества
[8]. Решение каждой из задач (4) выражается через подмультимножества ![]() ,
, ![]() и определяет лучшую бинарную декомпозицию
и определяет лучшую бинарную декомпозицию ![]() совокупности КП
совокупности КП ![]() по группе оценок, соответствующих характеристике
по группе оценок, соответствующих характеристике ![]() (
(![]() ). Пусть
). Пусть ![]() – граничное значение оценки по характеристике, определяющее границу между сгенерированными слагаемыми внутри каждой пары
– граничное значение оценки по характеристике, определяющее границу между сгенерированными слагаемыми внутри каждой пары ![]() и
и ![]() . Различные комбинации граничных оценок
. Различные комбинации граничных оценок ![]() для разных характеристик
для разных характеристик ![]() (
(![]() ) задают условия отнесения КП
) задают условия отнесения КП ![]() к классу
к классу ![]() и образуют возможные ОРПК КП вида (2). Граничные оценки
и образуют возможные ОРПК КП вида (2). Граничные оценки ![]() по характеристикам можно упорядочить по значениям расстояний
по характеристикам можно упорядочить по значениям расстояний ![]() . Для построения ОРПК целесообразно использовать граничные оценки
. Для построения ОРПК целесообразно использовать граничные оценки ![]() по характеристикам, занимающим первые места в ранжировке. Чем ближе значение расстояния
по характеристикам, занимающим первые места в ранжировке. Чем ближе значение расстояния ![]() к расстоянию
к расстоянию ![]() , тем более точной будет аппроксимация предварительной индивидуальной экспертной сортировки КП. Оценить качество аппроксимации по характеристике
, тем более точной будет аппроксимация предварительной индивидуальной экспертной сортировки КП. Оценить качество аппроксимации по характеристике ![]() (
(![]() ) можно по величине показателя аппроксимации
) можно по величине показателя аппроксимации ![]() , характеризующего важность этой характеристики в ОРПК:
, характеризующего важность этой характеристики в ОРПК:
![]() . (5)
. (5)
В итоге определяются ОРПК КП, показывающие, каким образом принимаются групповые классификационные решения, то есть какие характеристики оценивания действительно являются важными (поскольку присутствуют в правилах), и каковы граничные значения этих характеристик, влияющие на отнесение КП к тому или иному классу. При этом максимально возможное количество ОРПК КП равно количеству характеристик оценивания.
КП считается «правильно классифицированным», если ОРПК относит его к тому же классу, который был определен для этого КП в ходе предварительной индивидуальной экспертной сортировки. Оценка точности аппроксимации, обеспечиваемая ОРПК, рассчитывается как отношение количества КП, «правильно классифицированных» этим правилом к общему количеству КП. Очевидно, что если два правила ОРПК имеют одинаковую точность аппроксимации, то в качестве результирующего следует выбрать ОРПК с меньшим количеством характеристик оценивания. Искомое итоговое ОРПК должно включать граничные оценки ![]() (
(![]() ) по характеристикам, имеющим значения показателя аппроксимации
) по характеристикам, имеющим значения показателя аппроксимации ![]() , превышающие желаемый пороговый уровень
, превышающие желаемый пороговый уровень ![]() , и обеспечивающие необходимую точность аппроксимации [8]. По результатам анализа структуры ОРПК, сопоставляемых различным стратегиям оценивания, к использованию могут быть рекомендованы, например, те ОРПК (и, соответственно, стратегии), которые при одинаковом составе (количестве) выявленных характеристик оценивания, влияющих на принятие решения, имеют максимально большие значения показателя аппроксимации по этим характеристикам по формуле (5), а также характеризуются максимальной точностью аппроксимации совокупности КП этим ОРПК.
, и обеспечивающие необходимую точность аппроксимации [8]. По результатам анализа структуры ОРПК, сопоставляемых различным стратегиям оценивания, к использованию могут быть рекомендованы, например, те ОРПК (и, соответственно, стратегии), которые при одинаковом составе (количестве) выявленных характеристик оценивания, влияющих на принятие решения, имеют максимально большие значения показателя аппроксимации по этим характеристикам по формуле (5), а также характеризуются максимальной точностью аппроксимации совокупности КП этим ОРПК.
КП, отнесенные с помощью ОРПК, например, к классу «Принять КП к реализации», могут быть упорядочены с целью отбора для дальнейшего финансирования по удаленности от «антиидеального» (наихудшего) КП или по близости к «идеальному» (наилучшему) КП, которым все эксперты дали соответственно низшие и высшие оценки по всем характеристикам оценивания, присутствующим в ОРПК. В случае, когда в ОРПК учитываются все характеристики оценивания, «антиидеальный» и «идеальный» КП описываются с помощью мультимножеств ![]() и
и ![]() [8].
[8].
Задача упорядочения КП ![]() (
(![]() ) может быть сведена к задаче упорядочения соответствующих им мультимножеств
) может быть сведена к задаче упорядочения соответствующих им мультимножеств ![]() , например, по возрастанию величины расстояния
, например, по возрастанию величины расстояния ![]() , вычисляемого по формуле (3), что позволит упорядочить КП от худшего к лучшему [3, 8].
, вычисляемого по формуле (3), что позволит упорядочить КП от худшего к лучшему [3, 8].
Пусть КП ![]() хуже КП
хуже КП ![]() (
(![]() ), если
), если ![]() . Пусть КП
. Пусть КП ![]() и КП
и КП ![]() эквивалентны, и упорядочение КП является нестрогим, если
эквивалентны, и упорядочение КП является нестрогим, если ![]() .
.
Расстояние ![]() может быть вычислено как:
может быть вычислено как:
![]() , (6)
, (6)
при этом значения коэффициентов относительной важности ![]() (
(![]() ) могут быть определены, например, в соответствии с выводами, полученными при формировании ОРПК.
) могут быть определены, например, в соответствии с выводами, полученными при формировании ОРПК.
Тогда КП ![]() хуже КП
хуже КП ![]() (
(![]() ), если
), если ![]() .
.
Таким образом, задача упорядочения КП ![]() (
(![]() ) сводится к сравнению взвешенных сумм первых (худших) оценок КП по характеристикам оценивания
) сводится к сравнению взвешенных сумм первых (худших) оценок КП по характеристикам оценивания ![]() . Худшим является тот КП
. Худшим является тот КП ![]() , для которого сумма
, для которого сумма ![]() – наибольшая. Если некоторые КП
– наибольшая. Если некоторые КП ![]() (
(![]() ) эквиваленты, то имеет место частичное упорядочение КП, так как КП
) эквиваленты, то имеет место частичное упорядочение КП, так как КП ![]() «занимают» одно и то же место. Для упорядочения эквивалентных КП (и соответствующих им мультимножеств
«занимают» одно и то же место. Для упорядочения эквивалентных КП (и соответствующих им мультимножеств ![]() ), имеющих одинаковые суммы первых оценок
), имеющих одинаковые суммы первых оценок ![]() , необходимо вычислить для мультимножеств
, необходимо вычислить для мультимножеств ![]() (
(![]() ) взвешенные суммы вторых оценок КП по характеристикам оценивания
) взвешенные суммы вторых оценок КП по характеристикам оценивания ![]() и упорядочить КП от худшего к лучшему по убыванию сумм
и упорядочить КП от худшего к лучшему по убыванию сумм ![]() . Процедуру вычисления и сравнения сумм вторых, третьих и т.п. оценок КП по характеристикам оценивания необходимо выполнять до полного упорядочения всех КП (и соответствующих им мультимножеств) [3, 8]. Аналогичным образом может быть выполнено упорядочение КП
. Процедуру вычисления и сравнения сумм вторых, третьих и т.п. оценок КП по характеристикам оценивания необходимо выполнять до полного упорядочения всех КП (и соответствующих им мультимножеств) [3, 8]. Аналогичным образом может быть выполнено упорядочение КП ![]() (
(![]() ) по близости к «идеальному» (наилучшему) КП. При этом, если
) по близости к «идеальному» (наилучшему) КП. При этом, если ![]() , то КП
, то КП ![]() лучше КП
лучше КП ![]() . В общем случае результаты упорядочения КП
. В общем случае результаты упорядочения КП ![]() (
(![]() ) по удаленности от «антиидеального» (наихудшего) КП могут не совпадать с результатами упорядочения по близости к «идеальному» (наилучшему) КП из-за разных значений количеств экспертных оценок по характеристикам оценивания.
) по удаленности от «антиидеального» (наихудшего) КП могут не совпадать с результатами упорядочения по близости к «идеальному» (наилучшему) КП из-за разных значений количеств экспертных оценок по характеристикам оценивания.
При использовании лингвистического подхода к оцениванию КП целесообразно проанализировать варианты ОРПК, основанные на различных стратегиях оценивания, с целью выявления возможных перегруппировок характеристик оценивания, а также выявления изменения их значимости при использовании различных стратегий оценивания. Так же выбор той или иной стратегии оценивания может существенно повлиять на результаты упорядочения КП, отнесенных на основе ОРПК, например, к классу «Принять КП к реализации». Если сопоставить некоторой стратегии оценивания КП показатель ![]() (
(![]() ), то оценка, соответствующая этой стратегии, может быть вычислена как [6, 10]:
), то оценка, соответствующая этой стратегии, может быть вычислена как [6, 10]: ![]() . При
. При ![]() стратегия оценивания является чисто рискованной, при
стратегия оценивания является чисто рискованной, при ![]() стратегия оценивания является чисто консервативной, а при
стратегия оценивания является чисто консервативной, а при ![]() – нейтральной. При анализе различных стратегий оценивания в процессе вычислений для каждой стратегии автоматически формируется виртуальная лингвистическая шкала.
– нейтральной. При анализе различных стратегий оценивания в процессе вычислений для каждой стратегии автоматически формируется виртуальная лингвистическая шкала.
Экспериментальная часть. Результаты классификации и упорядочения КП, полученные на основе данных независимого предварительного индивидуального оценивания, выполненного 7 экспертами для группы из 15 КП по 4 характеристикам, подтвердили высокую объективность и адекватность принимаемых решений с применением предлагаемого лингвистического подхода. При выполнении предварительной индивидуальной сортировки каждый эксперт оценивал КП по 4 характеристикам: ![]() – «социально-экономическая значимость проекта для города и области»;
– «социально-экономическая значимость проекта для города и области»; ![]() – «конкурентоспособность проекта»;
– «конкурентоспособность проекта»; ![]() – «финансовый уровень предприятия-заявителя»;
– «финансовый уровень предприятия-заявителя»; ![]() – «актуальность и новизна проекта» [6], выставляя интервальные оценки по лингвистической шкале при
– «актуальность и новизна проекта» [6], выставляя интервальные оценки по лингвистической шкале при ![]() , и, кроме того, относил КП к одному из двух классов: «Принять КП к реализации» и «Отклонить КП». На рисунке 1 показаны оценки 15 КП по 4 характеристикам, выставленные 7 экспертами (на каждом изображении оценки экспертов расположены снизу вверх, начиная с 1-го). Результирующая принадлежность КП к классу определялась на основе данных предварительной индивидуальной сортировки КП по правилу простого большинства. При этом оказалось, что КП с номерами 1, 3, 4, 5, 6, 7, 11, 13, 14, 15 попали в класс «Принять КП к реализации», а КП с номерами 2, 8, 9, 10 – в класс «Отклонить КП». Для анализируемой совокупности КП с применением различных стратегий оценивания были сформированы итоговые ОРПК КП, получены результаты классификации КП с применением итогового ОРПК и списки упорядочения КП, отнесенных итоговым ОРПК к классу «Принять КП к реализации».
, и, кроме того, относил КП к одному из двух классов: «Принять КП к реализации» и «Отклонить КП». На рисунке 1 показаны оценки 15 КП по 4 характеристикам, выставленные 7 экспертами (на каждом изображении оценки экспертов расположены снизу вверх, начиная с 1-го). Результирующая принадлежность КП к классу определялась на основе данных предварительной индивидуальной сортировки КП по правилу простого большинства. При этом оказалось, что КП с номерами 1, 3, 4, 5, 6, 7, 11, 13, 14, 15 попали в класс «Принять КП к реализации», а КП с номерами 2, 8, 9, 10 – в класс «Отклонить КП». Для анализируемой совокупности КП с применением различных стратегий оценивания были сформированы итоговые ОРПК КП, получены результаты классификации КП с применением итогового ОРПК и списки упорядочения КП, отнесенных итоговым ОРПК к классу «Принять КП к реализации».

Рис. 1. Экспертные оценки конкурсных проектов по характеристикам оценивания
Таблица 1
ОРПК, позволяющие отнести КП к классу «Принять КП к реализации»
|
Правило |
|
|
|
|
Показатель аппроксимации |
|
1 |
2 или 3 |
– |
– |
– |
0,944 |
|
2 |
2 или 3 |
2 или 3 |
– |
– |
0,859 |
|
3 |
2 или 3 |
2 или 3 |
2 или 3 |
– |
0,831 |
|
4 |
2 или 3 |
2 или 3 |
2 или 3 |
2 или 3 |
0,803 |
Так, для случая, когда используется чисто рискованная стратегия оценивания (![]() ), множество аппроксимирующих граничных значений оценок
), множество аппроксимирующих граничных значений оценок ![]() по характеристикам, упорядоченное по убыванию значений расстояний
по характеристикам, упорядоченное по убыванию значений расстояний ![]() , может быть записано как:
, может быть записано как: ![]() , и, значит, наиболее важной для отнесения КП к классу «Принять КП к реализации» является характеристика
, и, значит, наиболее важной для отнесения КП к классу «Принять КП к реализации» является характеристика ![]() , а следующими по важности являются характеристики
, а следующими по важности являются характеристики ![]() ,
, ![]() и
и ![]() . В таблице 1 приведены ОРПК КП, сформированные в соответствии с множеством аппроксимирующих граничных значений оценок
. В таблице 1 приведены ОРПК КП, сформированные в соответствии с множеством аппроксимирующих граничных значений оценок ![]() по характеристикам.
по характеристикам.
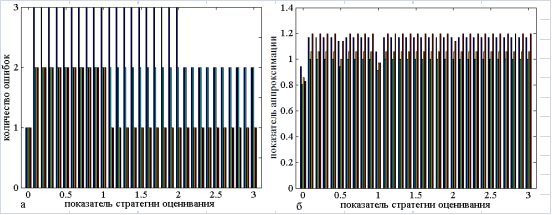
Рис. 2. Диаграмма:
а – для количества ошибок классификации в группах ОРПК при различных стратегиях оценивания;
б – для значений показателей аппроксимации характеристиками оценивания первоначальных индивидуальных сортировок КП при различных стратегиях оценивания
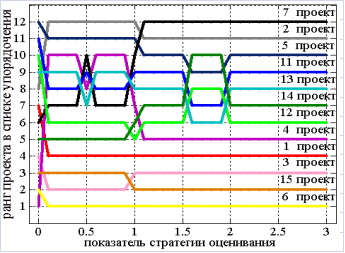
Рис. 3. Пример упорядочения КП от лучшего к худшему
При формировании ОРПК участвовали все 4 характеристики оценивания. При этом точные ОРПК отсутствуют. Так как все 4 приближенных ОРПК обеспечивают одинаковую точность аппроксимации данных предварительной индивидуальной сортировки КП на два класса (только КП № 2, попавший априори в класс «Отклонить КП», отнесен в результате аппроксимации ОРПК совокупности КП к классу «Принять КП к реализации»), то в качестве итогового ОРПК КП целесообразно выбрать 1-е ОРПК. Смена стратегии оценивания может привести к изменению номера ОРПК (к изменению количества характеристик, которые необходимо учитывать при выполнении классификации) и точности аппроксимации (количества ошибок классификации) итоговым ОРПК. В рассматриваемом примере оказалось, что при ![]() достаточно использовать 1-е ОРПК, учитывающее оценки только по одной характеристике, в качестве итогового; при
достаточно использовать 1-е ОРПК, учитывающее оценки только по одной характеристике, в качестве итогового; при ![]() – 2-е ОРПК, учитывающее оценки по двум характеристикам, а при
– 2-е ОРПК, учитывающее оценки по двум характеристикам, а при ![]() – 3-е ОРПК, учитывающее оценки по трем характеристикам. При этом количество ошибок классификации на основе ОРПК оказалось равным: при
– 3-е ОРПК, учитывающее оценки по трем характеристикам. При этом количество ошибок классификации на основе ОРПК оказалось равным: при ![]() и
и ![]() единице, а при
единице, а при ![]() – двум. На рисунке 2, а приведена диаграмма, демонстрирующая количество ошибок классификации в каждой группе из 4 ОРПК (при отображении правил слева направо, начиная с 1-го), соответствующей некоторой стратегии оценивания. Исходя из диаграммы на рисунке 2, б, могут быть сформированы рекомендации по применению тех или иных стратегий оценивания КП, в частности, может быть рекомендовано отказаться от стратегий с показателями
– двум. На рисунке 2, а приведена диаграмма, демонстрирующая количество ошибок классификации в каждой группе из 4 ОРПК (при отображении правил слева направо, начиная с 1-го), соответствующей некоторой стратегии оценивания. Исходя из диаграммы на рисунке 2, б, могут быть сформированы рекомендации по применению тех или иных стратегий оценивания КП, в частности, может быть рекомендовано отказаться от стратегий с показателями ![]() 0; 0,5; 1; 2, имеющих меньшие значения показателей аппроксимации по характеристикам оценивания КП (характеристики в каждой группе расположены слева направо, начиная с 1-й), особенно в случае, когда предполагается выполнение последующего упорядочения и отбора КП с целью финансирования.
0; 0,5; 1; 2, имеющих меньшие значения показателей аппроксимации по характеристикам оценивания КП (характеристики в каждой группе расположены слева направо, начиная с 1-й), особенно в случае, когда предполагается выполнение последующего упорядочения и отбора КП с целью финансирования.
На рисунке 3 приведен пример результатов упорядочения 12 КП (в том числе и КП № 2), отнесенных на основе ОРПК к классу «Принять КП к реализации», по удаленности от «антиидеального» КП при различных стратегиях оценивания КП при условии равновесности характеристик оценивания. Для анализируемых КП стратегии оценивания с ![]() =0; 0,1; 0,5; 0,6; 1; 1,1; 1,6; 2 являются «точками изменения» результатов упорядочения КП при движении с шагом 0,1 от стратегии оценивания с показателем
=0; 0,1; 0,5; 0,6; 1; 1,1; 1,6; 2 являются «точками изменения» результатов упорядочения КП при движении с шагом 0,1 от стратегии оценивания с показателем ![]() =0 к стратегии оценивания с показателем
=0 к стратегии оценивания с показателем ![]() =3. При этом при стратегиях оценивания, значения показателей
=3. При этом при стратегиях оценивания, значения показателей ![]() которых лежат в диапазонах: 0,1 – 0,4; 0,6 – 0,9; 1,1 – 1,5; 1,6 – 1.9; 2 – 3, результаты упорядочения КП остаются неизменными, но существенно отличаются друг от друга при смене диапазона или выборе стратегий оценивания с показателями
которых лежат в диапазонах: 0,1 – 0,4; 0,6 – 0,9; 1,1 – 1,5; 1,6 – 1.9; 2 – 3, результаты упорядочения КП остаются неизменными, но существенно отличаются друг от друга при смене диапазона или выборе стратегий оценивания с показателями ![]() =0; 0,5; 1.
=0; 0,5; 1.
Выводы. Предлагаемый лингвистический подход к принятию решений по классификации и упорядочению КП на основе инструментария теории мультимножеств предоставляет аналитику новые возможности для комплексного анализа КП, позволяющие рассмотреть различные стратегии принятия решений и выбрать наиболее оптимальную с точки зрения применяемого математического аппарата. При этом удается учесть все, в том числе и противоречащие друг другу, оценки экспертов.
Рецензенты:
Кузнецов А.Е., д.т.н., профессор, зам. директора НИИ «Фотон», ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань;
Овечкин Г.В., д.т.н., профессор кафедры вычислительной и прикладной математики, ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.
Библиографическая ссылка
Демидова Л.А., Соколова Ю.С. КОМПЛЕКСНЫЙ АНАЛИЗ КОНКУРСНЫХ ПРОЕКТОВ НА ОСНОВЕ ИНСТРУМЕНТАРИЯ ТЕОРИИ МУЛЬТИМНОЖЕСТВ С ПРИМЕНЕНИЕМ ЛИНГВИСТИЧЕСКОЙ ШКАЛЫ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15583 (дата обращения: 12.03.2026).



