Известно [6], что выход в зону соединения металлов при сварке давлением дефектов кристаллической решетки способствует образованию металлических связей между атомами соединяемых поверхностей. При этом дефекты кристаллической решетки являются активными центрами, на основе которых и происходит развитие взаимодействия соединяемых металлов при сварке давлением [9,10]. В зависимости от энергии и размера центра возмущения, в активированное состояние переходят не отдельные атомы, а большая их группа [6].
Точечные дефекты оказывают существенное влияние на свойства металла. Они участвуют во многих процессах, таких, как диффузия, рост пор в ходе пластической деформации и т.д. Через взаимодействие с дислокациями точечные дефекты влияют на механические свойства металла и на микроструктуру [4], особенно на микроструктуру тех металлов, которые подвержены различным внешним воздействиям [9,15], в том числе деформациям, что имеет место при сварке давлением. Одними из точечных дефектов кристаллической решетки являются дефекты в виде вакансий, которые вероятнее всего являются преобладающим типом дефектов для металлов, имеющих решетку ГЦК [7].
Из теории вакансий известно, что в условии равновесия кристалл обязан содержать определенное количество вакансий. Этот факт объясняется тем, что при образовании вакансии наряду с возрастанием энергии происходит увеличение энтропии, вследствие чего минимум общей свободной энергии наблюдается не для идеального кристалла, а для кристалла с вакансиями [1].
В процессе пластической деформации соединяемых металлов, что имеет место при сварке давлением, генерируется большое количество точечных дефектов - вакансий. Обычно концентрация деформационных вакансий составляет величину 10-5…10-6 даже для не очень больших скоростей деформаций и средних температур ![]() (
(![]() , где
, где ![]() – температура плавления металла) [22]. Равновесная концентрация вакансий с увеличением температуры возрастает, в частности, для Cu вблизи точки плавления она достигает 2∙10-4, для Al – 9,4∙10-4, для Au - 7,2∙10-4, для Ag – 1,7∙10-4 [16].
– температура плавления металла) [22]. Равновесная концентрация вакансий с увеличением температуры возрастает, в частности, для Cu вблизи точки плавления она достигает 2∙10-4, для Al – 9,4∙10-4, для Au - 7,2∙10-4, для Ag – 1,7∙10-4 [16].
Вышесказанное свидетельствует о важной роли дефектов кристаллической решетки, в частности, вакансий, как активных центров, с помощью которых может происходить развитие взаимодействия соединяемых металлов при сварке металлов давлением на стадии их объемного взаимодействия.
Постановка задачи исследования
Одной из гипотез образования соединения при сварке давлением, является так называемая энергетическая гипотеза А.П. Семенова [2,6,20]. Согласно этой гипотезе, непосредственный контакт соединяемых поверхностей, при котором расстояние между атомами соединяемых поверхностей имеет порядок параметра кристаллической решетки, еще не достаточен для проявления схватывания. Автор отмечает, что “…способность к схватыванию поликристаллического металла соответствует его определенному состоянию. Для проявления схватывания необходимо, чтобы энергия атомов, находящихся в контакте объемов металла, поднялась выше какого-то, определенного для данного металла уровня, который можно назвать “энергетическим порогом схватывания”. При этом ”…между поверхностями образуются металлические связи и поверхность раздела двух соприкасающихся объемов металла исчезает” [6,20].
Рассматривая эту гипотезу, предполагаем, что вакансии, являющиеся активными центрами, на основе которых происходит развитие взаимодействия соединяемых металлов при сварке давлением, дают определенный вклад в энергию активации процесса образования соединения, т.е. той энергии, которую необходимо обеспечить для преодоления энергетического порога схватывания металлов согласно гипотезе А.П. Семенова. Следовательно, представляется целесообразным определение энергии вакансий для ряда металлов с целью выявления в дальнейшем величины ее вклада в энергию активации процесса при образовании соединения металлов при сварке давлением.
Результаты исследования
Энергию вакансии определяют как экспериментальными методами (дилатометрический, калориметрический (теплоемкости), электросопротивления, аннигиляции позитронов и т.д.), так и теоретическими расчетами (вариационный метод, методы псевдопотенциала, псевдоиона и т.д.) [19].
При применении экспериментальных методов определения энергии вакансии достаточно сложно обеспечить в металле один вид дефектов и его комплексы, в частности, вакансий, поскольку в реальном металле присутствуют и другие точечные дефекты, например, примеси внедрения и замещения. Кроме того, в кристалле имеются более укрупненные дефекты, такие как дислокации, диклинации и границы зерен. Так как эти дефекты присутствуют в кристалле одновременно, то при выделении эффекта от комплекса одного вида дефекта возникают определенные трудности. Поэтому экспериментальное определение энергий вакансий становится затруднительным и даже проблематичным. Поэтому при использовании разных экспериментальных методов получаются различные величины энергий вакансий [15,24].
Кроме этого, измерения физических характеристик в экспериментальных методах, обусловленных дефектами, проводят обычно в условиях, когда фиксированы температура ![]() и давление
и давление ![]() . Поскольку при обычных условиях
. Поскольку при обычных условиях ![]() (
(![]() – энергия вакансии), то часто говорят об энергии точечных дефектов, в частности, вакансий, хотя измеряют фактически энтальпию [19], т.е. значение энтальпии фактически приравнивают к энергии вакансии.
– энергия вакансии), то часто говорят об энергии точечных дефектов, в частности, вакансий, хотя измеряют фактически энтальпию [19], т.е. значение энтальпии фактически приравнивают к энергии вакансии.
В связи с вышесказанным, характеристики точечных дефектов, в том числе и энергии вакансии, и их комплексов получают в большинстве случаев в настоящее время преимущественно из теоретических расчетов [15].
При использовании теоретических расчетов для определения энергии вакансии следует выбрать наиболее адаптированную методику с точки зрения удобства использования применительно к сварке давлением и хорошо согласующейся с результатами, имеющимися в литературе, а также позволяющей рассчитать энергию вакансии при разных температурах. Обычно при расчетах энергии вакансии температурой пренебрегают, мотивируя это слабой зависимостью энергии вакансии от температуры [15]. Но не ясно, как это выражается в количественном отношении, и если учесть, что сварка металлов давлением возможно при различной температуре соединяемых металлов, то целесообразно использовать для определения энергии вакансии методику, учитывающую зависимость энергии вакансии от температуры.
Ниже представлены наиболее простые зависимости для определения энергии вакансии применительно к моделированию процессов сварки давлением. Экспериментально установлено [25], что для ГЦК металлов выполняется следующее соотношение:
![]() , (1)
, (1)
где ![]() – постоянная Больцмана,
– постоянная Больцмана, ![]() – температура плавления металла.
– температура плавления металла.
Известна и другая зависимость энергии вакансии от температуры [11]:
![]() . (2)
. (2)
Представленные выше формулы достаточно просты, но не учитывают конкретных характеристик кристаллических решеток для разных металлов, квантовые эффекты и зависят только от температуры плавления металла.
Применительно к сварке давлением наиболее адаптирована и легко применима методика определения энергии вакансии проф. М.Н. Магомедова [14]. Согласно этой методики твердое и жидкое состояние вещества моделируется с единых позиций. Система рассматривается как виртуальная структура из ![]() (где
(где ![]() – число атомов,
– число атомов, ![]() – число вакансий) ячеек одинакового размера, в которой
– число вакансий) ячеек одинакового размера, в которой ![]() ячеек вакантны. При этом предполагается, что структура из
ячеек вакантны. При этом предполагается, что структура из ![]() v ячеек аналогична структуре кристаллической решетки данного вещества. Это так называемое “изоструктурное приближение решеточной модели”. Кроме этого считается, что атомы в системе могут находиться в двух состояниях: в локализованном и в делокализованном. В локализованном состоянии атом локализован в ячейке виртуальной решетки и имеет только колебательные степени свободы. В делокализованном состоянии атому доступен весь объем системы, и он имеет только трансляционные степени свободы. Поэтому энергия вакансии в данном случае рассматривается в виртуальной решеточной структуре.
v ячеек аналогична структуре кристаллической решетки данного вещества. Это так называемое “изоструктурное приближение решеточной модели”. Кроме этого считается, что атомы в системе могут находиться в двух состояниях: в локализованном и в делокализованном. В локализованном состоянии атом локализован в ячейке виртуальной решетки и имеет только колебательные степени свободы. В делокализованном состоянии атому доступен весь объем системы, и он имеет только трансляционные степени свободы. Поэтому энергия вакансии в данном случае рассматривается в виртуальной решеточной структуре.
Вероятность образования вакансии в решеточной модели простого вещества в данном случае можно определить по формуле [13,14]:
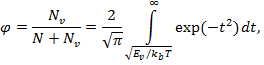 где
где ![]() – количество вакантных ячеек,
– количество вакантных ячеек, ![]() – количество ячеек в решетке,
– количество ячеек в решетке, ![]() – энергия вакантного узла,
– энергия вакантного узла, ![]() – температура,
– температура, ![]() – время.
– время.
Данная формула справедлива для ГЦК, ОЦК и алмазной упаковки атомов. Энергию вакансии можно определить по формуле [12-14]:
![]() (3)
(3)
где
![]() , (4)
, (4)
![]() , (5)
, (5)
![]() – доля атомов, находящихся в D-состоянии;
– доля атомов, находящихся в D-состоянии; ![]() – первое координационное число при
– первое координационное число при ![]() ;
; ![]() – коэффициент упаковки структуры из
– коэффициент упаковки структуры из ![]() сферических ячеек;
сферических ячеек; ![]() – масса атома;
– масса атома; ![]() - где
- где ![]() - постоянная Планка;
- постоянная Планка; ![]() – температура Дебая;
– температура Дебая; ![]() – расстояние между центрами ближайших ячеек в безвакансионной системе. Функция
– расстояние между центрами ближайших ячеек в безвакансионной системе. Функция ![]() учитывает квантовые эффекты и вычисляется по формуле [12-14]:
учитывает квантовые эффекты и вычисляется по формуле [12-14]:
![]() , (6)
, (6)
где ![]()
![]() – температура Эйнштейна в безвакансионной системе. Температуру Эйнштейна рассчитывали по формуле [4]:
– температура Эйнштейна в безвакансионной системе. Температуру Эйнштейна рассчитывали по формуле [4]:
![]() ,
,
где ![]() – мерность системы (для нашего случая
– мерность системы (для нашего случая ![]() ).
).
Для твердой фазы металлов ![]() [4,17], формулу (3) можно преобразовать в вид:
[4,17], формулу (3) можно преобразовать в вид:
![]() (7)
(7)
C учетом (7) и подстановки ![]() в формулу (5) получаем:
в формулу (5) получаем:
![]() . (8)
. (8)
Рассмотрим определение энергии вакансии для следующих наиболее распространенных металлов: Cu, Al, Ag и Au. Эти металлы характеризуются ГЦК решеткой, у которой ![]() =12. Энергию вакансии вычисляли при обычных условиях для
=12. Энергию вакансии вычисляли при обычных условиях для ![]() =300 К.
=300 К.
Масса атома Cu ![]() =106∙10-27 кг, а расстояние между центрами ближайших ячеек в безвакансионной системе
=106∙10-27 кг, а расстояние между центрами ближайших ячеек в безвакансионной системе ![]() =2,56 Å [8,11]. В литературе при расчетах принимают различные значения температуры Дебая для Cu, в частности, 310 К [5,26]; 315 К (полученные из данных по теплоемкости), и 329 К (полученные из данных по скорости звука)[4]; 340 К [23]. Энергию вакансии рассчитывали при минимальном и максимальном значениях температуры Дебая, значения которых имеются в литературе, т.е. 310 К и 340 К. Формула (8) дает значения энергии вакансии в Дж., а для перевода Дж. в эВ. воспользуемся известным соотношением: 1эВ=1,602∙10-19 Дж. Расчеты по формуле (8) с учетом (6) показали, что энергия вакансии для Сu при
=2,56 Å [8,11]. В литературе при расчетах принимают различные значения температуры Дебая для Cu, в частности, 310 К [5,26]; 315 К (полученные из данных по теплоемкости), и 329 К (полученные из данных по скорости звука)[4]; 340 К [23]. Энергию вакансии рассчитывали при минимальном и максимальном значениях температуры Дебая, значения которых имеются в литературе, т.е. 310 К и 340 К. Формула (8) дает значения энергии вакансии в Дж., а для перевода Дж. в эВ. воспользуемся известным соотношением: 1эВ=1,602∙10-19 Дж. Расчеты по формуле (8) с учетом (6) показали, что энергия вакансии для Сu при ![]() =300 К и
=300 К и ![]() =310 К составляет приблизительно 0,8 эВ (по формуле (6) функция
=310 К составляет приблизительно 0,8 эВ (по формуле (6) функция ![]() ≈0,953), а при
≈0,953), а при ![]() ==300 К и
==300 К и ![]() =340 К энергия образования вакансии составляет приблизительно 0,95 эВ (по формуле (6) функция
=340 К энергия образования вакансии составляет приблизительно 0,95 эВ (по формуле (6) функция ![]() ≈0,944).
≈0,944).
Аналогичные расчеты энергии вакансии были выполнены и для Al. Масса атома Al ![]() =44,803∙10-27 кг. Расстояние между центрами ближайших ячеек в безвакансионной системе для Al
=44,803∙10-27 кг. Расстояние между центрами ближайших ячеек в безвакансионной системе для Al ![]() =2,86 Å [8,11]. В литературе можно встретить разные значения температуры Дебая: 390 К [5,26]; 394 К (полученные из данных по теплоемкости), и 399 К (полученные из данных по скорости звука) [4]; 375 К [23]. Энергию вакансии рассчитывали также при минимальном и максимальном значении температуры Дебая, т.е. 375 К и 399 К. Вычисления по формуле (8) показали, что энергия вакансии для Al при
=2,86 Å [8,11]. В литературе можно встретить разные значения температуры Дебая: 390 К [5,26]; 394 К (полученные из данных по теплоемкости), и 399 К (полученные из данных по скорости звука) [4]; 375 К [23]. Энергию вакансии рассчитывали также при минимальном и максимальном значении температуры Дебая, т.е. 375 К и 399 К. Вычисления по формуле (8) показали, что энергия вакансии для Al при ![]() ==300 К и
==300 К и ![]() =375 К составляет приблизительно 0,6 эВ (по формуле (6) функция
=375 К составляет приблизительно 0,6 эВ (по формуле (6) функция ![]() ≈0,933), а при
≈0,933), а при ![]() ==300 К и
==300 К и ![]() =399 К энергия вакансии составляет приблизительно 0,67 эВ (по формуле (6) функция
=399 К энергия вакансии составляет приблизительно 0,67 эВ (по формуле (6) функция ![]() ≈0,925).
≈0,925).
Вычисления энергии вакансии для Au выполнялись с учетом массы атома ![]() =327,08∙10-27 кг и расстояния между центрами ближайших ячеек в безвакансионной системе
=327,08∙10-27 кг и расстояния между центрами ближайших ячеек в безвакансионной системе ![]() =2,88 Å [8,11]. В литературе в различных расчетах принимают разные значения температуры Дебая для Au, в частности, 178 К [5,26]; 170 К [4,23]. Энергию вакансии рассчитывали для этих температур Дебая. Расчет по формуле (8) показал, что энергия вакансии для Au при
=2,88 Å [8,11]. В литературе в различных расчетах принимают разные значения температуры Дебая для Au, в частности, 178 К [5,26]; 170 К [4,23]. Энергию вакансии рассчитывали для этих температур Дебая. Расчет по формуле (8) показал, что энергия вакансии для Au при ![]() ==300 К и
==300 К и ![]() =170 К составляет приблизительно 0,97 эВ (по формуле (6) функция
=170 К составляет приблизительно 0,97 эВ (по формуле (6) функция ![]() ≈0,985), а при
≈0,985), а при ![]() ==300 К и
==300 К и ![]() =178 К энергия образования вакансии составляет приблизительно 1,06 эВ (по формуле (6) функция
=178 К энергия образования вакансии составляет приблизительно 1,06 эВ (по формуле (6) функция ![]() ≈0,984).
≈0,984).
Вычисления энергии вакансии для Ag выполнялись с учетом массы атома Ag ![]() =179,1∙10-27 кг и расстояния между центрами ближайших ячеек в безвакансионной системе
=179,1∙10-27 кг и расстояния между центрами ближайших ячеек в безвакансионной системе ![]() =2,89 Å [8,11]. В литературе при расчетах принимают различные значения температуры Дебая для Ag, в частности, 221 К [5,26]; 215 К (полученные из данных по теплоемкости), и 212 К (полученные из данных по скорости звука) [4]; 230 К [23]. Энергию вакансии рассчитывали при минимальном и максимальном значении температуры Дебая, т.е. для 212 К и 230 К. Вычисления по формуле (8) показали, что энергия вакансии для Ag при
=2,89 Å [8,11]. В литературе при расчетах принимают различные значения температуры Дебая для Ag, в частности, 221 К [5,26]; 215 К (полученные из данных по теплоемкости), и 212 К (полученные из данных по скорости звука) [4]; 230 К [23]. Энергию вакансии рассчитывали при минимальном и максимальном значении температуры Дебая, т.е. для 212 К и 230 К. Вычисления по формуле (8) показали, что энергия вакансии для Ag при ![]() =300 К и
=300 К и ![]() =212 К составляет приблизительно 0,82 эВ (по формуле (6) функция
=212 К составляет приблизительно 0,82 эВ (по формуле (6) функция ![]() ≈0,977), а при
≈0,977), а при ![]() =300 К и
=300 К и ![]() =230 К энергия вакансии составляет приблизительно 0,96 эВ (по формуле (6) функция
=230 К энергия вакансии составляет приблизительно 0,96 эВ (по формуле (6) функция ![]() ≈0,973).
≈0,973).
Вычисленные значения энергии вакансии для четырех металлов по формулам (1), (2) и (8), а также данные, имеющиеся в литературе, представлены в таблице.
Энергии вакансии для металлов Cu, Al, Au и Ag
|
Металл |
|
|
|
|
|
|
Теоретические данные |
Экспериментальные данные |
||||
|
Cu |
0,8 (θD =310 К), 0,95 (θD =340 К) |
0,93 |
1,17 |
1,05 [4], 0,9 [3], 0,81…1,2 [25], 0,81…0,95 [19],
|
1,28 [16], 1,22 [26], 0,98…1,3 [19], 1,22* [18], 0,9 [3], 1,27 [15], 1,17 [21] |
|
Al |
0,6 (θD =375 К), 0,67 (θD =399 К) |
0,64 |
0,8 |
0,39…1,56 (2,94 по методу точечных ионов) [19], 0,65 [4] |
0,67 [16], 0,66 [26], 0,62…0,79 [19], 0,66* [18], 0,75 [21] |
|
Au |
0,97 (θD =170 К), 1,06 (θD =178 К) |
0,92 |
1,15 |
0,87 [4], 0,6 [3], 0,6…0,77 [25], 0,62…0,77 [19] |
0,97 [26], 0,95 [16], 0,92…1 [19], 0,67 [3], 0,95 [21], 0,97* [18] |
|
Ag |
0,82 (θD =212 К), 0,96 (θD =230 К) |
0,85 |
1,06 |
1 [4], 0,6 [3] 0,6…0,92 [25], 0,72…1,13 [8]
|
1,1 [26], 1,13 [16], 0,99…1,16 [19], 1,1* [18], 0,8 [3], 1,10 [21] |
* - Автор не указывает, как получено значение энергии вакансии: теоретически или экспериментально.
Выводы
Сравнение вычисленных энергий вакансии по формуле (8) с теоретическими и экспериментальными данными, имеющимися в литературе, свидетельствуют о хорошей их сходимости. Использование в расчетах разного значения температуры Дебая дает разницу в вычислениях энергии вакансии, достигающей 15%.
Применительно к сварке давлением для теоретической оценки энергии вакансии целесообразно использовать методику проф. М.Н. Магомедова, учитывающую температуру нагрева металлов. Это позволит в дальнейшем оценить вклад энергии вакансии в энергию активации образования соединения металлов при моделировании процессов сварки давлением.
Рецензенты:
Сидоров В.Н., д.т.н., профессор, заведующий кафедрой, МГТУ им. Н.Э. Баумана, Калужский филиал, г. Калуга.
Антонюк Ф.И., д.т.н., профессор, МГТУ им. Н.Э. Баумана, Калужский филиал, г. Калуга.
Библиографическая ссылка
Латыпов Р.А., Булычев В.В., Зыбин И.Н., Коротков В.В. АНАЛИЗ МЕТОДИК РАСЧЕТА ЭНЕРГИИ ВАКАНСИИ В МЕТАЛЛАХ ПРИМЕНИТЕЛЬНО К МОДЕЛИРОВАНИЮ ПРОЦЕССОВ СВАРКИ ДАВЛЕНИЕМ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15580 (дата обращения: 12.03.2026).



