Задача повышения скорости метаемого элемента является актуальной задачей. Классическая схема выстрела практически исчерпала свои возможности в рамках повышения скоростей метаемых элементов, поэтому в настоящее время активно предлагаются принципиально новые схемы метания. Одной из таких схем, удачно сочетающей в себе классический подход к процессу выстрела и использование разделяемого заряда является схема с присоединенными ускоряемыми камерами подгона (СПК). В данном случае рассматривается схема с одной присоединенной камерой. Подробно данная схема рассматривается в [8]. В газодинамическом приближении [2] математическая модель, описывающая процессы, протекающие при выстреле, в системах СПК, с использованием комбинированной системы координат [6], имеет следующий вид:

где t – время, x – координата, p – давление, r – плотность газопороховой смеси, u – скорость газопороховой смеси, e внутренняя энергия единицы объёма газа, ![]() - скорость подвижного поршня, S – площадь поперечного сечения канала, z – относительная толщина сгоревшего свода, y – сгоревший объём частицы топлива, Ik – импульс топлива, c,l – коэффициенты формы частиц топлива, d – плотность топлива, k – адиабата пороховых газов, a - коволюм,
- скорость подвижного поршня, S – площадь поперечного сечения канала, z – относительная толщина сгоревшего свода, y – сгоревший объём частицы топлива, Ik – импульс топлива, c,l – коэффициенты формы частиц топлива, d – плотность топлива, k – адиабата пороховых газов, a - коволюм, ![]() - потенциал топлива,
- потенциал топлива, ![]() - сила топлива.
- сила топлива.
Решение данной системы уравнений проводится методом конечно-разностной схемы с соответствующими начальными и граничными условиями [4]. Исследование функции зависимости скорости метаемого элемента от зависимых параметров показало, что функция не является монотонной и имеет достаточно большое количество локальных оптимумов, не смотря на это, проводились попытки оптимизировать параметры систем СПК с использованием метода покоординатного спуска [1], которые показали хорошие результаты. Однако наличие таких недостатков обуславливает возможность применения эволюционных алгоритмов для оптимизации параметров систем СПК [5].
Процессы, протекающие в системах СПК, зависят от следующих параметров:
-
геометрия системы – сюда относят характеристики конкретной рассчитываемой системы, в том числе длина ствола, площади сечений ствола в различных точках, а также начальное положение подвижного поршня и метаемого элемента;
-
массы основного и дополнительных зарядов системы;
-
импульсы энергетических составов основного и дополнительного заряда;
-
масса подвижного поршня и метаемого элемента;
-
время задержки воспламенения дополнительного заряда.
Конечно же, это далеко не полный перечень параметров, которые могли бы повлиять на скорость метаемого элемента, но наиболее существенные с точки зрения моделирования процессов в системах СПК. Остальные параметры могут быть учтены при проведении дальнейших исследований.
Перейдем к постановке задачи оптимизации. Необходимо найти параметры системы, при которых дульная скорость метаемого элемента была бы максимальна, при следующих ограничениях:
-
давления газов внутри системы не должно превышать 1000 МПа;
-
плотность заряжания, то есть отношение массы заряда к допустимому объему не должно превышать 0,9 кг/дм3;
-
масса подвижного поршня должна находиться в пределах от 50 до 100 граммов;
-
координата задержки воспламенения присоединенного заряда должна располагаться между координатой поршня и максимальной координатой поршня до вылета метаемого элемента из ствола.
При этом изменяться будут следующие параметры: масса основного заряда (ω1), масса дополнительного заряда (ω2), импульс энергетического состава основного заряда (Ik1) и дополнительного заряда (Ik2), координата задержки зажигания присоединенного заряда (Tз) и масса подвижного поршня (Q). Или в виде формулы:
![]()
Ограничения для ![]() линейные, а нелинейные ограничения на давления задаются с помощью формулы:
линейные, а нелинейные ограничения на давления задаются с помощью формулы:
![]()
где hi – ограничения по давлениям на соответствующих границах расчётных областей.
Основа применения генетических алгоритмов для поиска оптимальных решений лежит в применении принципов эволюции биологических систем при решении технических задач. Для генетических алгоритмов характерны такие заимствованные из биологии понятия как особь, популяция, хромосома и тому подобные. Так, например, некоторое потенциальное решение представляет собой особь, выраженную набором хромосом – набором параметров. В процессе эволюции (поиска оптимального решения) используются три основных генетических оператора: отбор, мутация и скрещивание. В зависимости от того как будут проходить эти операции, а также от количества особей в популяции и количества поколений участвующих в поиске оптимального решения зависит насколько быстро будет получен и выявлен оптимальный набор параметров оптимизируемой системы. Существуют общие закономерности характерные для генетических алгоритмов, однако каждая задача требует в этом плане индивидуального подхода и является отдельным исследованием.
Существует несколько способов кодирования каждого решения для использования его в генетическом алгоритме. Чаще всего каждый параметр представляет собой строку генов, а ген особи, в свою очередь, представляется в виде двоичной цифры (0 или 1), а в качестве параметров решения могут быть выбраны значения различных типов. Самый простой вариант преобразования применяется в задачах, когда параметры решения являются целыми числами. В этом случае достаточно перевести число из десятичной системы счисления в десятичную систему. В нашем же случае параметры задаются в виде вещественных чисел. Здесь для кодирования могут быть применены различные подходы, так например можно сначала привести число к экспоненциальной форме и отдельно кодировать мантиссу числа и его порядок, однако этот способ накладывает некоторые ограничения на используемые генетические операторы. Другим способом представления вещественных чисел является использование двоичного вектора. Определим необходимую точность представления вещественного числа (R) через количество знаков после запятой (p) и его диапазон [a; b], при этом следует отметить, что при точности менее одного знака после запятой, значение коэффициента p должно браться со знаком «-». Тогда для кодирования всех числе необходимо будет h=|b-a|*10p уникальных наборов или log2h битов для каждой хромосомы, а строка описывающая хромосому будет соответствовать вещественному числу R=D*|b-a|/2h+a, где D – десятичное представление двоичной строки хромосомы. Применение данного кодирования вещественных чисел позволит использовать классический генетический алгоритм, так же как и при работе с целыми числами. Такой метод кодирования имеет некоторые недостатки. Одним из них является не соответствие расстояний между точками и расстоянием Хемминга между двоичными представлениями этих чисел. Так, например, расстояние для точек 15 и 16 будет равно 1, а для их двоичных преставлений 01111 и 10000 – 5. Одним из способов преодоления этого недостатка является использование при кодировании кода Грея. Те же самые числа в коде Грея будут выглядеть как 01000 и 11000 с расстоянием Хемминга 1. Подробно алгоритм преобразования двоичного числа в код Грея рассмотрен в [7].
При решении задачи оптимизации с помощью генетического алгоритма используются следующие обозначения. Особь – набор параметров оптимизируемой функции, а также значение функции для этих параметров, которое характеризует приспособленность особи. Хромосома – параметр функции, представляет собой набор генов.
Определим операторы, которые будут применяться в оптимизационной задаче. В качестве оператора отбора (селектор) будет использоваться отбор на основе усечения. Этот метод не имеет аналогов в естественной эволюции и обычно используется для больших популяций (>100). При этом сначала отбираемые особи упорядочиваются согласно значениям целевой функции. Затем, в качестве родителей выбирают пары, которые производят потомков. При этом методе используется параметр – порог отсечения или интенсивность отбора, показывающий долю, которая отбирается в качестве родителей. Выберем в качестве значения порога 50%. В качестве оператора скрещивания (кроссинговер) будет использоваться одноточечный кроссинговер. Здесь случайно выбирается точка скрещивания и производится обмен фрагментами хромосом родителей после точки скрещивания. В результате появляются два потомка, каждый из которых содержит признаки обоих родителей. В качестве оператора мутации используется классическая двоичная мутация. У мутирующей особи случайным образом выбирается ген, который инвертируется.
Упрощенный алгоритм оптимизации параметров СПК с использованием эволюционных вычислений приведен на рисунке 1.
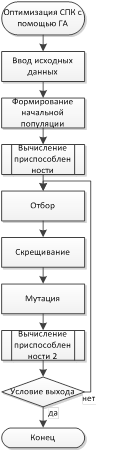
Рис. 1. Упрощенная блок-схема оптимизации параметров системы СПК
В блоке ввода исходных данных вводятся нижние и верхние границы зависимых параметров системы, ограничения давления газов на стенки и дно пусковой трубы. Эти данные будут использоваться в следующем блоке при формировании начальной популяции. Каждая особь случайным образом получает набор хромосом характеризующих параметры системы с учетом фиксированных границ, а также этот набор преобразуется в код Грея. В подпроцессе вычисления приспособленности происходит решение ПЗВБ для данных параметров, результатом решения становятся скорость метаемого элемента и максимальные значения давления в четырех разных точках: на дне ствола (P1), на подвижном поршне слева (P2), на подвижном поршне справа (P3), и на метаемом элементе (P4). При превышении максимальных значений давления по сравнению с допустимыми, происходит уменьшение приспособленности системы с использованием штрафной функции вида:
![]()
После вычисления приспособленности выполняется отбор особей, приспособленность которых выше средней, все остальные особи отбрасываются. Оставшиеся особи учувствуют в скрещивании для повышения численности популяции до постоянного значения. Далее в блоке мутации случайные 0,5% особей популяции мутируют – случайный бит из набора особи инвертируется. После этого производится расчет приспособленности особей, которые вновь появились при скрещивании и мутировавших особей. Такой алгоритм позволяет не проводить лишних вычислений, при этом следует сказать, что самым ресурсоемким процессом данного алгоритма является решение ПЗВБ. Далее при достижении условий выхода происходит выход или в ином случае управление передается блоку осуществляющему отбор и так далее. В качестве условий выхода могут быть использованы различные подходы, в нашем же случае условие выхода было сложным. Программа выводила на печать параметры лучших 10% решений через каждое поколений, и пользователь решал, следует продолжить поиск оптимума или прекратить.
В таблице приведены результаты оптимизации в сравнении с результатами, полученными с использованием метода покоординатного спуска.
|
Параметр СПК |
Генетический алгоритм |
Метод покоординатного спуска |
|||||
|
Входные граничные значения |
Результаты первого поколения |
Итоговые результаты |
Входные граничные значения |
Итоговые результаты |
|||
|
Нижняя граница |
Верхняя граница |
Нижняя граница |
Верхняя граница |
||||
|
w1, г |
100 |
132 |
118,5 |
115 |
100 |
132 |
132 |
|
w2, г |
75 |
104 |
90,5 |
90 |
54 |
105 |
104 |
|
Ik1, МПа*с |
0,250 |
0,600 |
0,33930 |
0,27668 |
0,100 |
2,500 |
0,494 |
|
Ik2, МПа*с |
0,080 |
0,180 |
0,11968 |
0,11411 |
0,010 |
1,000 |
0,157 |
|
Tз, дм |
9 |
10 |
9,35 |
9,08 |
9 |
10 |
9,4 |
|
Q, г |
50 |
100 |
51,8 |
75,4 |
10 |
100 |
75 |
|
U, б/р |
|
|
1,401 |
1,5023 |
|
|
1,461 |
|
P1, б/р |
|
0,235 |
0,327 |
0,233 |
|
0,235 |
0,241 |
|
P2, б/р |
|
0,235 |
0,275 |
0,205 |
|
0,235 |
0,220 |
|
P3, б/р |
|
0,524 |
0,387 |
0,504 |
|
0,524 |
0,436 |
|
P4, б/р |
|
0,524 |
0,440 |
0,522 |
|
0,524 |
0,545 |
где б/р обозначены безразмерные параметры.
В результате оптимизации были получены параметры системы, начальная скорость метаемого элемента которой значительно превышает скорости, которые получены для классических систем с теми же ограничениями. Не секрет, что основной движущей силой действующей на поршень и метаемый элемент является давление пороховых газов. В итоговом результате давления P1, P3, P4 приблизились к заданным граничным значениям, давление P2 находится в пределах 15% от максимального.
Основываясь на данных результатах, можно предположить, что применение генетического алгоритма позволит оптимизировать параметры более сложной системы с двумя подгонными камерами [3] по десяти оптимизируемым параметрам с шестью нелинейными ограничениями давлений на границах системы СПК.
В результате проведенных исследований можно сделать следующие выводы:
-
Использование генетических алгоритмов позволяет проводить оптимизацию параметров немонотонных функций имеющих достаточно большое количество локальных оптимумов.
-
Применение генетических алгоритмов для оптимизации параметров систем СПК позволяет получить более хорошие решения по сравнению с решениями полученными методом покоординатного спуска.
-
В результате оптимизации удалось найти параметры системы СПК обеспечивающие прирост в начальной скорости метаемого элемента до 30% по сравнению с классическими системами.
Рецензенты:
Талалов С.В., д.ф.-м.н., профессор, заместитель ректора - директор Института математики, физики и информационных технологий ФГБОУ ВПО "Тольяттинский государственный университет"; Российская федерация, Самарская область, город Тольятти.
Сафронов Александр Иванович, д.ф.-м.н., с. н. с. ВАК, профессор кафедры Нанотехнологии, материаловедение и механика, Машиностроительного института ФГБОУ ВПО "Тольяттинский государственный университет"; Российская федерация, Самарская область, город Тольятти.
Библиографическая ссылка
Зоркин В.А. ИСПОЛЬЗОВАНИЕ ГЕНЕТИЧЕСКОГО АЛГОРИТМА ДЛЯ ОПТИМИЗАЦИИ ПАРАМЕТРОВ СИСТЕМЫ С УСКОРЯЕМОЙ ПРИСОЕДИНЕННОЙ КАМЕРОЙ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15474 (дата обращения: 23.02.2026).



