Выведена функциональная зависимость вероятности ошибки от отношения сигнал/помеха, боковых пиков огибающей автокорреляционной (![]() ) и взаимокорреляционной функции (
) и взаимокорреляционной функции (![]() ) сигналов, коэффициента неортогональности (
) сигналов, коэффициента неортогональности (![]() ) сигналов, адекватность которой подтверждается возможностью получения в частных случаях известных зависимостей для вероятности ошибки схемы приема по методу квадратичного суммирования. Результаты исследований показали, что наиболее помехоустойчивой является ортогональная система (
) сигналов, адекватность которой подтверждается возможностью получения в частных случаях известных зависимостей для вероятности ошибки схемы приема по методу квадратичного суммирования. Результаты исследований показали, что наиболее помехоустойчивой является ортогональная система (![]() = 0), удовлетворяющая условиям разделения лучей (
= 0), удовлетворяющая условиям разделения лучей (![]() = 0,
= 0, ![]() = 0). При увеличении
= 0). При увеличении ![]() ,
, ![]() и
и ![]() до 0.2 вероятность ошибки возрастает сравнительно мало и отклонение от ортогональности и условий разделения лучей можно скомпенсировать небольшим увеличением мощности сигнала. Когда
до 0.2 вероятность ошибки возрастает сравнительно мало и отклонение от ортогональности и условий разделения лучей можно скомпенсировать небольшим увеличением мощности сигнала. Когда ![]() ,
, ![]() и
и ![]() стремятся к единице, сигналы становятся неразличимыми. Так при
стремятся к единице, сигналы становятся неразличимыми. Так при ![]() = 0.5,
= 0.5, ![]() = 0.5 и
= 0.5 и ![]() = 0.5 уже никаким увеличением мощности передатчика скомпенсировать падение верности нельзя. Полученные результаты позволят выбрать оптимальные системы сигналов для использования в двухлучевых каналах связи.
= 0.5 уже никаким увеличением мощности передатчика скомпенсировать падение верности нельзя. Полученные результаты позволят выбрать оптимальные системы сигналов для использования в двухлучевых каналах связи.
Эффективным средством борьбы с замираниями, вызванными дискретной многолучевостью, является разнесенный прием с разделением лучей по времени прихода и последующим их сложением, при этом наиболее сложными для существующих систем передачи информации являются двухлучевые каналы связи [4].
При осуществлении разнесенного приема чаще всего применяют некогерентные методы. При построении некогерентных решающих схем не используются априорные сведения о начальной фазе принимаемого сигнала. Это позволяет в большинстве случаев существенно упростить схемную реализацию ценой некоторого увеличения вероятности ошибок [3]. Анализ показывает, что оптимальные схемы приема, как правило, очень сложны и требуют априорного знания статистических параметров канала и их распределений, которые могут быть получены лишь при помощи достоверных и в то же время относительно кратковременных измерений принимаемых сигналов. В связи с этим далее все расчеты будем проводить для простой, но достаточно эффективной схемы приема по методу квадратичного суммирования [1].
Удобным критерием оценки помехоустойчивости систем передачи информации является вероятность ошибки при приеме символа сообщения. Однако существующий научно-методический аппарат оценки помехоустойчивости обладает рядом недостатков. Формулы для расчета вероятности ошибки получены с допущениями:
-
не учтены одновременно боковые пики автокорреляционной функции (АКФ) и взаимокорреляционной функции (ВКФ) сигналов;
-
при расчетах считается, что сигналы разных символов сообщения ортогональны в усиленном смысле по всем каналам приема.
В связи с этим необходимо провести совершенствование методики расчета вероятности ошибки схем приема по методу квадратичного суммирования, работающих в двухлучевых каналах связи.
Целью исследований является анализ влияния корреляционных характеристик сигналов на вероятность ошибки для схемы приема двоичных сигналов по методу квадратичного суммирования. Полученные результаты позволят выбрать оптимальные системы сигналов для использования в двухлучевых каналах связи. В связи с этим необходимо провести совершенствование методики расчета вероятности ошибки схем приема по методу квадратичного суммирования, работающих в двухлучевых каналах связи.
Материал и метод исследования. Усовершенствованная методика отличается от известной, приведенной в [1], наличием дополнительных ограничений – боковые пики АКФ rАКФ и боковые пики ВКФ rВКФ отличны от нуля:
ρАКФ≠0, ρВКФ≠0,
необходимость введения которых объясняется тем, что при использовании в качестве сигналов-переносчиков реальных ансамблей сигналов с малой базой боковые пики КФ могут быть довольно значительными.
Принимаемый сигнал для рассматриваемого канала удобнее представлять через квадратурные составляющие коэффициентов передачи лучей
![]()
тогда принимаемый сигнал имеет вид
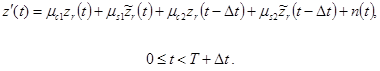
где μi и θi – соответственно амплитудная и фазовая составляющие коэффициента передачи i-го луча, zr(t) – передаваемый сигнал, Т – длительность сигнала, Δt – задержка второго луча относительно первого.
Для случая приема сигналов по методу квадратичного суммирования правило принятия решения при передаче первого сигнала можно представить в виде [1]:
![]() (1)
(1)
где
![]() ,
,![]() ,
,![]() ,
,
![]()
Принимаемый сигнал имеет вид:
![]() .
.
Случайные величины, входящие в каждое слагаемое суммы (1), имеют нормальное распределение вероятности [1] и равны:
![]() (2)
(2)
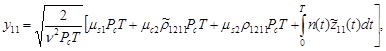 (3)
(3)
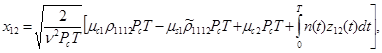 (4)
(4)
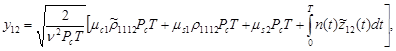 (5)
(5)
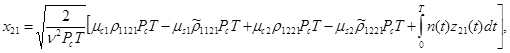 (6)
(6)
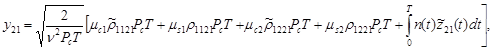 (7)
(7)
![]() (8)
(8)
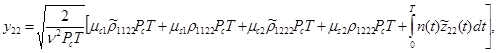 (9)
(9)
где ![]()
![]() – спектральная плотность мощности шума, Рс – мощность сигнала,
– спектральная плотность мощности шума, Рс – мощность сигнала, ![]()
![]() – боковой пик огибающей АКФ,
– боковой пик огибающей АКФ, ![]() – боковые пики огибающей ВКФ (
– боковые пики огибающей ВКФ (![]() ),
), ![]() – комплексный коэффициент неортогональности в усиленном смысле,
– комплексный коэффициент неортогональности в усиленном смысле, ![]() .
.
Из анализа соотношений (2) – (9) следует, что
1. Величины ![]() – случайные величины, распределенные по нормальному закону, т.к. представляют собой линейную комбинацию нормально распределенных случайных величин
– случайные величины, распределенные по нормальному закону, т.к. представляют собой линейную комбинацию нормально распределенных случайных величин ![]()
![]() и n(t) с нулевым математическим ожиданием [5].
и n(t) с нулевым математическим ожиданием [5].
2. Величины ![]() зависят от коэффициентов передачи лучей
зависят от коэффициентов передачи лучей ![]() и
и ![]() , энергии сигнала РсТ, а также от боковых пиков огибающей АКФ –
, энергии сигнала РсТ, а также от боковых пиков огибающей АКФ – ![]() , ВКФ -
, ВКФ - ![]() и коэффициента неортогональности сигналов
и коэффициента неортогональности сигналов ![]() .
.
Плотность вероятности квадратичной формы x находится при помощи преобразования Фурье от характеристической функции [1]:
![]()
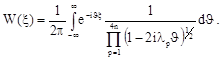 (10)
(10)
где ![]() – собственные числа матрицы К×А, n=2 – число лучей, К – матрица ковариаций случайных величин (2) – (9), А – матрица квадратичной формы
– собственные числа матрицы К×А, n=2 – число лучей, К – матрица ковариаций случайных величин (2) – (9), А – матрица квадратичной формы ![]() [1]:
[1]:
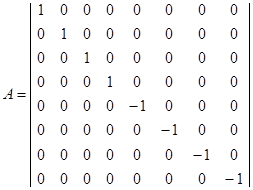 .
.
В зависимости от значений элементов матрицы К собственные числа матрицы К×А могут иметь двойную кратность, т.е. всего будет два собственных числа кратности 2n каждое, и парную кратность, т.е. всего будет 2n различных собственных значения. Для этих случаев плотность вероятности получена в [1]. Рассмотрим случай, когда собственные числа матрицы К×А имеют парную кратность, при этом два собственных числа будут действительные, а два – комплексно сопряженные. Выражение (10) можно привести к виду:
![]() . (11)
. (11)
Вычислив интеграл, получим искомую плотность вероятности:
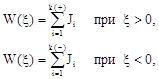 (12)
(12)
где ![]()
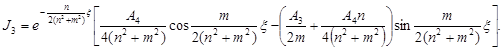
Обозначения ![]() и
и ![]() указывают на то, что суммирование ведется соответственно по всем положительным и по всем отрицательным действительным собственным числам
указывают на то, что суммирование ведется соответственно по всем положительным и по всем отрицательным действительным собственным числам ![]() и действительным частям комплексных собственных чисел. Постоянные А1, А2, А3, А4 определяются по методу неопределенных коэффициентов [2], n и m соответственно действительная и мнимая части комплексного собственного числа.
и действительным частям комплексных собственных чисел. Постоянные А1, А2, А3, А4 определяются по методу неопределенных коэффициентов [2], n и m соответственно действительная и мнимая части комплексного собственного числа.
При одинаковых вероятностях появления используемых сигналов вероятность ошибки будет равна при передаче первого сигнала:
![]() . (13)
. (13)
Результаты исследований. Анализируя выражения (10) – (12), можно сделать вывод, что плотность вероятности квадратичной формы определяется собственными числами ![]() , зависящими от величин (2) – (9), которые зависят от величины коэффициента неортогональности в усиленном смысле
, зависящими от величин (2) – (9), которые зависят от величины коэффициента неортогональности в усиленном смысле ![]() , а также от величины боковых пиков огибающей автокорреляционной функции
, а также от величины боковых пиков огибающей автокорреляционной функции ![]() и взаимокорреляционной функции
и взаимокорреляционной функции ![]() .
.
На рисунке 1 изображена зависимость вероятности ошибки от h2 при различных значениях боковых пиков огибающей автокорреляционной rАКФ, взаимокорреляционной функций ![]() и коэффициента неортогональности
и коэффициента неортогональности![]() .
.
Как видно из рисунка, наиболее помехоустойчивой является ортогональная система (![]() = 0), удовлетворяющая условиям разделения лучей (
= 0), удовлетворяющая условиям разделения лучей (![]() = 0,
= 0, ![]() = 0). При увеличении
= 0). При увеличении ![]() ,
, ![]() и
и ![]() до 0.2 вероятность ошибки возрастает сравнительно мало, и отклонение от ортогональности и условий разделения лучей можно скомпенсировать небольшим увеличением мощности сигнала. Когда
до 0.2 вероятность ошибки возрастает сравнительно мало, и отклонение от ортогональности и условий разделения лучей можно скомпенсировать небольшим увеличением мощности сигнала. Когда ![]() ,
, ![]() и
и ![]() стремятся к единице, сигналы становятся неразличимыми. Так, при
стремятся к единице, сигналы становятся неразличимыми. Так, при ![]() = 0.5,
= 0.5, ![]() = 0.5 и
= 0.5 и ![]() = 0.5 уже никаким увеличением мощности передатчика скомпенсировать падение верности нельзя.
= 0.5 уже никаким увеличением мощности передатчика скомпенсировать падение верности нельзя.
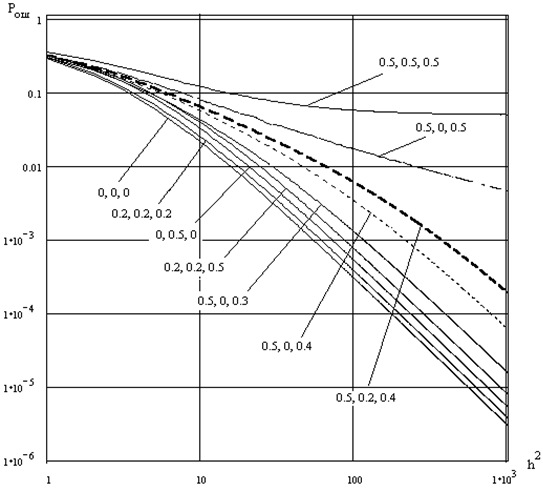
График зависимости Рош от h2 с учетом коэффициентов ![]() ,
, ![]() ,
, ![]()
Выводы. Таким образом, вероятность ошибки для схемы квадратичного суммирования зависит от величины коэффициента неортогональности в усиленном смысле ![]() , а также от величины боковых пиков огибающей автокорреляционной функции и взаимокорреляционной функции
, а также от величины боковых пиков огибающей автокорреляционной функции и взаимокорреляционной функции ![]() ,
, ![]() .
.
Рецензенты:
Калмыков И.А., д.т.н., профессор, профессор кафедры информационной безопасности автоматизированных систем Северо-Кавказского федерального университета, г. Ставрополь;
Шуваев А.В., д.э.н., профессор, профессор кафедры информационных систем Ставропольского государственного аграрного университета, г. Ставрополь.
Библиографическая ссылка
Гайчук Д.В., Гайчук В.Ю. АНАЛИЗ ВЛИЯНИЯ КОРРЕЛЯЦИОННЫХ ХАРАКТЕРИСТИК СИГНАЛОВ НА ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ СХЕМЫ РАЗНЕСЕННОГО ПРИЕМА С РАЗДЕЛЕНИЕМ ЛУЧЕЙ ПО ВРЕМЕНИ ПРИХОДА // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15434 (дата обращения: 04.02.2026).



